Исследование динамики осадков в Зерноградском районе

Зерноградский район относится к зоне неустойчивого увлажнения с преобладанием засушливых лет. Так, в [1] указано, что за период с 1930-го по 1970-й годы. 20 лет наблюдался недобор осадков в весенне-летний период и 13 лет было влажных, показатели остальных были около нормы. В осенне-зимний период 18 лет характеризовались недобором осадков против 15-ти влажных. В связи с этим особую актуальность приобретает изучение закономерностей изменения количества выпадающих осадков. Особый интерес здесь представляет анализ весенне-летних осадков в период активной вегетации полевых культур. В первую очередь, интересно количественное изучение периодичностей в выпадении осадков.

Для решения поставленной задачи необходимо применение широкого спектра независимых методов количественного анализа временных рядов измеренных значений выпавших осадков.

Для анализа нами был использован ряд значений осадков, выпавших за месяц, в Зерноградском районе за период с января 1944 года по декабрь 1996 года включительно. В работе [2] нами уже проводилось подобное исследование, ныне дополненное результатами вейвлет-анализа. Анализ периодичностей, наблюдаемых в рассматриваемом ряде осадков, производился четырьмя независимыми методами: методом периодограмм (амплитудных спектров), методом автокорреляционных спектров (спектров мощности), методом анализа автокорреляционной функции и методом вейвлет-анализа. Общая теория и методика применения первых трех методов для анализа различных временных рядов изложены в ряде фундаментальных работ, например, [3…4], и поэтому здесь не приводятся.

Представлены только полученные результаты и дается их метеорологическая интерпретация.

Вейвлет-преобразование одномерного сигнала состоит в разложении ряда значений функции / ( t ) по базису ¥ (( t-b ) /а ), сконструированному из обладающей определенными свойствами солитоноподобной функции (вейвлета) ¥ ( t ). Свойства вейвлет-функций подробно описаны в [5]. Наиболее важными свойствами вейвлет-функции являются: быстрое затухание ¥ ( t ) при | t | ^ да , равенство нулю хотя бы нулевого момента и ограниченная норма функции Y ( t ).

Базис конструируется с помощью переносов ( b - параметр сдвига) и масштабных преобразований ( а - масштабный коэффициент) вейвлет-функции. Каждая из функций этого базиса характеризует как определенную пространственную (временную) частоту, так и ее локализацию в физическом пространстве (времени).

Параметр t для ряда динамики отождествляется со временем. В этом случае масштабный коэффициент а является величиной, определяющей характерное время (временной масштаб) процесса, а параметр сдвига b соответствует времени.

Аналитически выражение для вейвлет-преобразования имеет вид да

W ( a , b ) = a '   - J ^ (( t - b ) / a ) • f ( t ) • dt

-да

В результате вейвлет-преобразования одномерного ряда получаем двумерный массив амплитуд вейвлет-преобразования – значений коэффициентов W ( a,b) в пространстве ( a,b ) = (масштаб, локализация).

В силу свойств анализирующего вейвлета обеспечивается хорошая локализация спектра коэффициентов W ( a,b ) как в области сдвигов ( b ), так и в области масштабов ( а ). Кроме того, из солитоноподоб-ности вейвлета следует важное преимущество вейвлет-анализа перед другими подобными методами, например, СВАНом – отсутствие априорных представлений о периодичности и амплитудных характеристиках анализируемого ряда.

Так как вейвлет-преобразование есть скалярное произведение анализирующего вейвлета на заданном масштабе и анализируемого ряда, то коэффициенты W ( a,b ) содержат информацию как о вейвлете, так и о ряде. Выбор анализирующего вейвлета определяется характером ряда и тем, какую информацию необходимо извлечь из анализируемого ряда.

Для решения задачи об оптимальном выборе анализирующего вейвлета в геомагнетизме требуется серьезный теоретический анализ и большой объем расчетных работ с использованием модельных рядов

и реальных рядов различной морфологии. Частично такой анализ проделан в работах [6…9]. В результате установлено, что для исследования параметров апериодических возмущений магнитного поля предпочтителен реальный MHAT-вейвлет (Мексиканская шляпа), представляющий собой вторую производную от функции Гаусса. Аналитическое выражение этого вейвлета имеет вид

¥ ( t) = (1 - t ²) • exp( - t ²/2). (2)

MHAT-вейвлет имеет узкий энергетический спектр и два равных нулю момента (нулевой и первый). Поэтому он хорошо приспособлен для анализа сложных рядов, имеющих как периодические, так и импульсные составляющие, что характерно для рядов данных социально-экономических показателей.

Для оценки степени периодичности процесса более подходит комплексный вейвлет Морле в виде

^(t ) = exp

г

v

t^г В ^²

• exp(i^T t),

здесь с т - параметр, позволяющий регулировать частотное и временное разрешение вейвлета;

го у - параметр с размерностью частоты.

При увеличении с улучшается разрешение вейвлета по масштабному коэффициенту a (т.е. по величине характерных масштабов анализируемых особенностей), но одновременно ухудшается разрешение по параметру сдвига b (т.е. по временной локализации особенностей). Параметр гоу характеризует «настройку» вейвлета по масштабному коэффициенту a и связь полученного значения характерного масштаба процесса с периодом данного процесса.

При использовании комплексного анализирующего вейвлета в результате вейвлет-преобразования получаются двумерные массивы значений модуля комплексных коэффициентов вейвлет-преобра-зования и их фазы [5]:

W (a, b ) = |W (a, b )• exp[z ф(а, b )] (4)

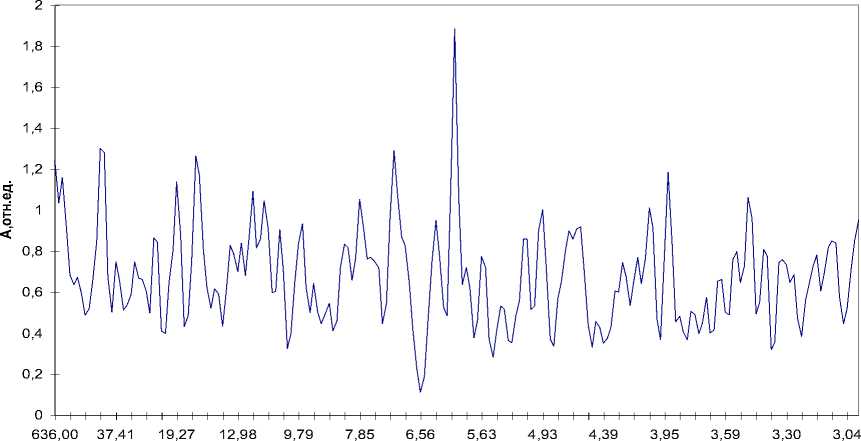
Месяцы

Рис. 1. Амплитудный спектр осадков в Зерноградском районе

Это дает дополнительные возможности для анализа квазипериодических составляющих изучаемого показателя.

В связи с тем, что основываясь на морфологии анализируемого ряда данных и общих закономерностях выпадения осадков, исходный ряд можно было считать стационарным, предварительных операций подготовки ряда (фильтрации, удаления тренда и т.п.) не проводилось.

На рисунке 1 представлен амплитудный спектр осадков. Легко видеть, что на фоне большого количества менее интенсивных максимумов на рисунке выделяется интенсивный максимум на периоде 6 месяцев.

На рисунке 2 представлен спектр мощности осадков. Следует отметить, что методика получения спектров мощности такова, что здесь интенсивность максимума пропорциональна квадрату спектральной мощности. В связи с этим наиболее интенсивный максимум, приходящийся на период 6 месяцев, выделился существенно сильнее по сравнению с другими максимумами, чем в спектре, полученном по методу периодограмм.

На рисунке 3 представлен график зависимости автокорреляционной функции от величины временного сдвига. На графике наблюдаются резкие максимумы при сдвигах, кратных 6 и 12 месяцам.

12 d

10 о of

636,00  37,41   19,27   12,98   9,79    7,85    6,56    5,63    4,93    4,39    3,95    3,59    3,30    3,04

Месяцы

Рис. 2. Спектр мощности осадков в Зерноградском районе

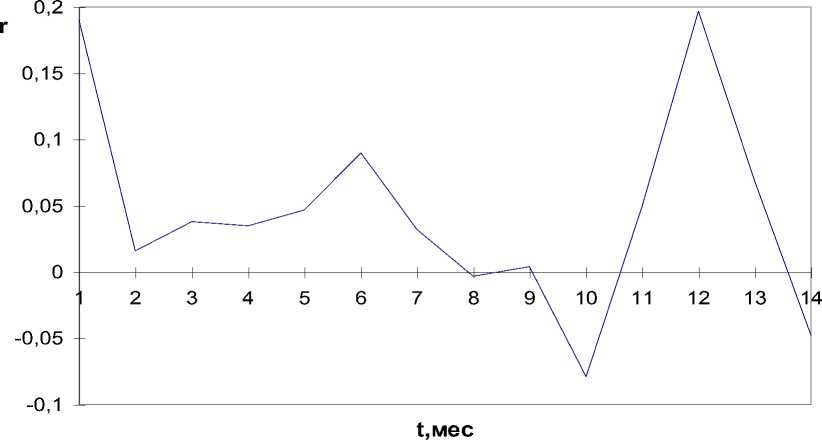
Рис.3. График зависимости автокорреляционной функции осадков от величины временного сдвига в месяцах

Таким образом, полученные тремя независимыми методами результаты указывают на наличие в осадках, выпадающих в Зерноградском районе, ярко выраженные периодичности с 6- и 12-месячными интервалами.

Далее, для определения характера зависимости количества выпавших осадков от времени года и проверки устойчивости полученных периодичностей методом наложенных эпох были получены средние значения осадков для 6- и 12-месячных интервалов. За начало обоих интервалов принимался январь. Таким образом, для 12-месячного интервала полученные результаты представляют собой среднемесячные значения осадков за период с 1944-го по 1996-й годы. Полученные среднемесячные значения осадков представлены в таблице 1.

Таблица 1

Среднемесячные значения осадков в Зерноградском районе за период с января 1944 г. по декабрь 1996 г., мм

янв.	февр.	март	апр.	май	июнь	июль	авг.	сент.	окт. нояб.	дек.
44	36	33	39	49	65	56	43	39	37   46	54

При построении 6-месячного интервала зависимости осадков от времени года суммировались для каждого года следующие пары месяцев: январь-июль, февраль-август, март-сентябрь, апрель-октябрь, май-ноябрь и июнь-декабрь. Полученные для 6-месячного интервала средние значения осадков за период с 1944-го по 1996-й годы представлены в таблице 2.

Таблица 2

Среднемесячные значения осадков в Зерноградском районе для 6-месячного интервала за период с января 1944 г. по декабрь 1996 г., мм

янв.–июль	февр.–авг.	март–сент.	апр.–окт.	май–нояб.	июнь–дек.
50	40	36	38	48	59

Представленные в таблице 2 результаты также наглядно показывают, что 6-месячная периодичность устойчиво наблюдается в среднемесячных осадках в Зерноградском районе.

Анализ таблиц 1 и 2 показывает, что максимум среднемесячных осадков приходится на июнь-июль и зимние месяцы.

Кроме средних значений среднемесячных осадков большой интерес также представляют вариансы и стандартные от- клонения их значений. Методика расчета вариансы и дисперсии представлена в работах [10–12].

Варианса позволяет оценить размах вариаций в значениях осадков и, соответственно, максимальные и минимальные значения осадков за рассматриваемый интервал времени. Максимальные и минимальные значения среднемесячных осадков за рассматриваемый интервал времени представлены в таблице 3.

Таблица 3

Минимальные и максимальные среднемесячные значения осадков в Зерноградском районе за период с января 1944 г. по декабрь 1996 г., мм

янв.	февр.	март	апр.	май	июнь	июль	авг.	сент.	окт.	нояб.	дек.
max 100	79	82	142	116	167	154	179	153	121	137	145
min 7	3	5	1	7	2	2	6	0	4	3	5

Знание стандартного отклонения отдельного измерения позволяет оценить величину интервала, в пределах которого будут лежать с заданной вероятностью возможные значения следующих измерений осадков. Иначе говоря, это позволяет с определенной вероятностью предсказывать по уже имеющимся данным следующие возможные значения среднемесячных осадков.

Собственно значения стандартных отклонений позволяют определять возможные значения ожидаемых осадков в пределах интервала (X -AX,Xc + AX) с вероятностью 68%. Полученные значения стандартных отклонений представлены в таблице 4.

Таблица 4

Стандартные отклонения среднемесячных значенийосадков в Зерноградском районе за период с января 1944 г. по декабрь 1996 г., мм

янв. февр.	март	апр.	май	июнь	июль	авг.	сент.	окт.	нояб.	дек.
25   20	19	28	27	42	35	32	35	25	32	32

Полученные большие значения вари-ансы и стандартного отклонения сравнительно со средними значениями указывают на существенную нестабильнось количества выпадающих среднемесячных осадков из года в год в данном месяце.

Так, например, в весенне-летние месяцы количество выпадающих осадков с 68-процентной вероятностью может колебаться: в мае – от 22 до 76 мм, в июне – от 23 до 107 мм, в августе – от 21 до 91 мм.

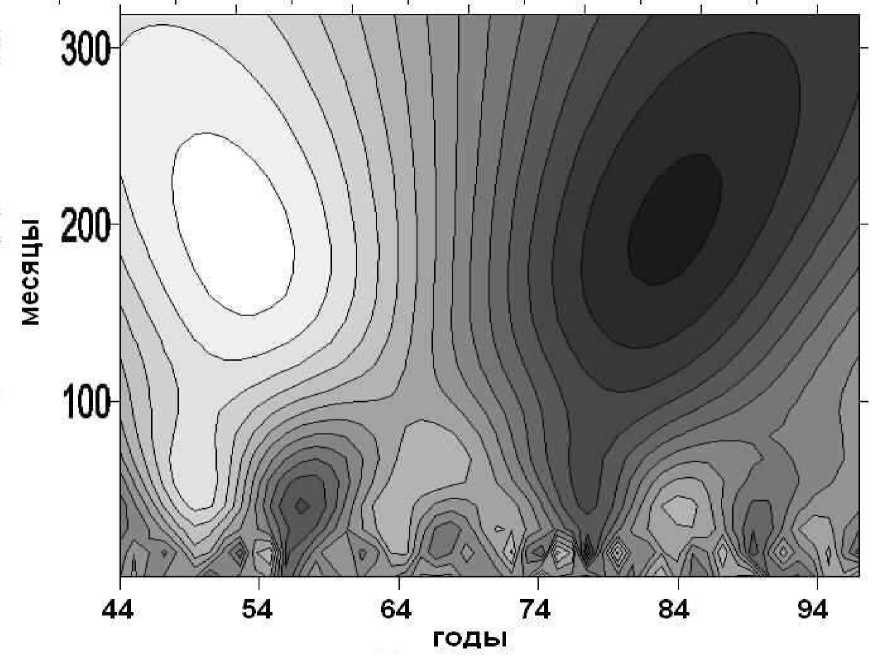
годы

На рисунке 4 представлена картина вейвлет-коэффициентов осадков. На картине выделяются отрицательный (светлый) и положительный (темный) экстремумы с масштабом порядка 200 месяцев с максимумами в начале 50-х и середине 80-х годов соответственно. Исследуемый ряд слишком короток, чтобы обсуждать вопрос о систематической повторяемости минимумов и максимумов осадков с таким ха- рактерным временем, но на рассматриваемом интервале такой масштаб изменения величины среднемесячного выпадения осадков присутствует.

В области малых масштабов выделяются максимумы с характерными временами порядка 40 месяцев в 57–58 годах и порядка 20 месяцев в 66–68 годах.

Для масштабов порядка нескольких месяцев наблюдается практически непре- рывная последовательность знакопеременных особенностей. Это указывает на существенные колебания осадков, наблюдающиеся в данном масштабе характерных времен.

В целом, картина вейвлет-коэффици-ентов позволяет обнаружить изменения уровней осадков с характерными временами порядка 20 лет и, для малых масштабов, подтверждает результаты, полученные вышеназванными методами.

И, наконец, с целью определения систематической тенденции к изменению количества выпадающих осадков в Зерноградском районе было рассчитано скользящее среднее со сглаживанием в 6, 12, 24 и 48 месяцев и сдвигом в один месяц. Выбор интервала сглаживания определялся наличием четко выраженных 6- и 12-месячных периодичностей в выпадении среднемесячных осадков в районе.

Анализ сглаженных таким образом данных показал, что существующая незначительная тенденция к увеличению количества среднемесячных осадков в Зерноградском районе (около 4 мм в год) сопровождается значительными флуктуациями и, соответственно, не может в ближайшее время учитываться для хозяйственного использования.

Выводы

Проведен количественный анализ закономерностей выпадения осадков в Зерноградском районе. Полученные результаты демонстрируют эффективность использованной методики для анализа подобных количественных закономерностей.

В осадках, выпадающих в Зерноградском районе, наблюдаются ярко выраженные периодичности с 6- и 12-месячными интервалами. Максимум среднемесячных осадков приходится на июнь-июль и зимние месяцы.

Количество выпадающих среднемесячных осадков из года в год в данном месяце характеризуется значительными отклонениями от средней величины, составляющими порядка 60…70% от среднего.

Для анализируемого интервала отмечаются изменения уровней осадков с ха- рактерными временами порядка 20 лет.

Хозяйственно значимой устойчивой тенденции к изменению среднемесячных осадков в районе не наблюдается.