Исследование долговременных асимптотик вероятности выживания частиц, диффундирующих в цилиндрических порах с ловушками

Исследование выполнено за счёт гранта Российского научного фонда № 2421-00356,

Проблема диффузии частиц в средах с поглощающими ловушками изучалась во многих работах [1-3]. Интерес обусловлен как ожидаемыми новыми особенностями в транспорте частиц, так и различными приложениями. В задаче диффузионных процессов в средах с ловушками возникает характерная длина – расстояние между ловушками и, соответственно, в динамике соответствующее время диффузии на расстояние порядка длины между ловушками. В одномерном случае оно равно:

t c = ( Dc ² J^{- 1} .

Здесь D — коэффициент диффузии, а с — концентрация ловушек, в одномерном случае расстояние между ловушками равно обратной концентрации. В работе [4] подробно исследовался случай захвата на поглощающие ловушки, случайно распределенных в пространстве, диффундирующих частиц. Было показано, что вероятность выживания частиц W ( t ; c ) на малых временах t <<  t с , где t_c = ( Dc ² ) , (здесь D — коэффициент диффузии, с — концентрация ловушек в одномерном случае) убывает по экспоненциальному закону.

Однако на больших временах асимптотика вероятности выживания определяется существованием достаточно больших областей, свободных от поглощающих ловушек, и носит дробно - экспоненциальный характер:

W ( t ; c ) « W 0 exp

f-71

< tc J

,

W ( t ; c ) к W 0

/         1/2( Dtc2 ]

I 3п )

exp

\

3п1/2(Dtc2)1/3 ^

В настоящей статье исследованы долговременные асимптотики вероятности выживания частиц, диффундирующих в цилиндрических областях с ловушками, расположенными на поверхности цилиндров.

Статья построена следующим образом. Во втором пункте статьи сформулирована постановка задачи, кратко описаны алгоритмы и методы численного моделирования, а также приводятся характеристики посевов ловушек. В третьем пункте изложены основные результаты численного эксперимента. В четвертом пункте обсуждаются особенности долговремен -ных асимптотик вероятности выживания активных частиц. В Заключении обсуждаются результаты.

1    Постановка задачи. Алгоритмы моделирования

Как говорилось выше, в статье рассмотрена задача захвата частиц, диффундирующих в полых цилиндрических областях с захватом на ловушки, расположенных на поверхности цилиндров. Радиус и высота цилиндрической поры задаются в процессе моделирования и могут быть изменены. Ловушки расположены на стенах поры случайным образом - см рис. 1а) и рис 1б) при разных степенях концентрации ловушек. Поскольку уравнение диффузии уравнение первого порядка по времени, то динамика протекающих диффузионных процессов определяется начальным условием в нулевой момент времени, когда имеются только N-частицы с однородной плотностью и граничными условиями на вершине цилиндра в плоскости Z = 0. Такая постановка соответствует распространению свободного кислорода, назовем О-частицами, в порах материала, в котором расположены случайным образом ловушки — С-частицы. Аналогичная задача рассматривалась в работе [5], однако там было использовано одномерное приближение с тремя типами частиц (дополнительно учитывался связанный кислород). В настоящей работе использована трехмерная геометрия - поры материала в виде цилиндра, что более соответствует геометрии low k материалов. Эти low k материалы являются одним из основных изолирующих материалов, используемыми в современной наноэлектронике.

1.1    Алгоритм моделирования. Диффузионные процессы и движение частиц

Опишем кратко алгоритм моделирования диффузии частиц в цилиндрических порах с ловушками. Направление движения выбирается произвольным образом генератором случайных чисел . При этом соблюдается ряд условий: а) после выбора направления движения проверяется свобод- но ли место в новой координате частицы, если место «свободно» то частица двигается в неё, иначе остаётся на своём месте. b) при достижении нижней или верхней границы цилиндра частицы «отражаются», то есть возвращаются в исходное положение. c) цилиндрическая поверхность достигается, когда на срезе по координате z расстояние от центра окружности превышает радиус цилиндра. В этом случае, происходит «отражение». Для генерации случайных чисел был использован алгоритм «Вихрь Мерсенна».

1.2    Размещение ловушек

Ловушки для захвата частиц размещались на цилиндрической поверхности пор. Координаты для ловушек, расположенных на цилиндрической поверхности выбирались следующим образом: случайным образом выбиралась координата Z – высота расположения на оси цилиндра, затем случайно выбирался угол и вычислялись координаты X и Y. Полученные координаты округлялись до целого значения отбрасыванием дробной части. Таким образом ловушки образуют «пояс» вокруг рабочей области. Это хорошо видно на проекции ловушек на плоскость Z=0 (Рис.1).

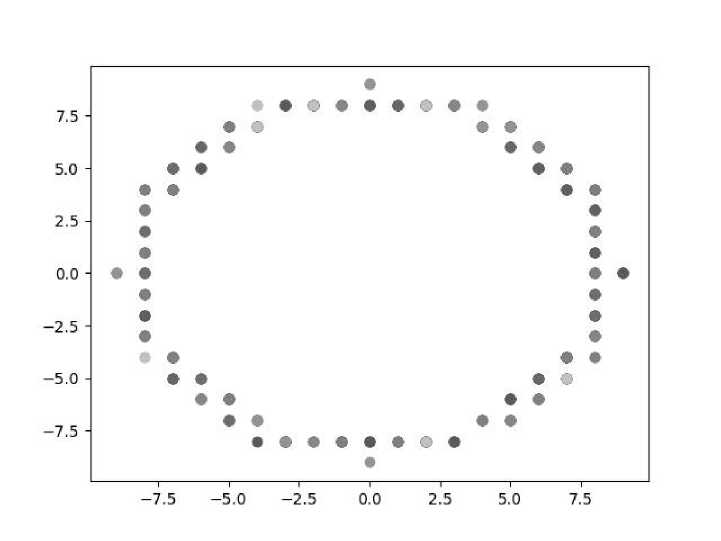
Рис. 1. Проекция расположения ловушек на поверхности цилиндра

Типичные примеры расположения ловушек представлены на рис. 2.12.2.

Рис. 2.1. Число ловушек N=1000

Рис. 2.2. Число ловушек N=10000

2    Процесс моделирования и результаты численного моделирования

Для моделирования диффузии были сгенерированы различные конфигурации ловушек, при этом число ловушек менялось от 1000 до 10000 с шагом 1000 см. рис. 2. Данные по числу активных частиц фиксировались через каждые 1000 числа шагов по времени (число итераций) для указанных конфигураций ловушек. Далее полученные данные по конфигурациям были усреднены и построен график изменения количества активных частиц от времени (числа итераций).

2.1    Асимптотическое поведение на больших временах

Проанализируем более подробно графики, на которых отображена зависимость медианы числа активных частиц от числа шагов по времени (итераций) при различных концентрациях ловушек. На рисунках 3 и 4 представлены графики изменения усредненного числа активных частиц (медиана) от времени (количества итераций).

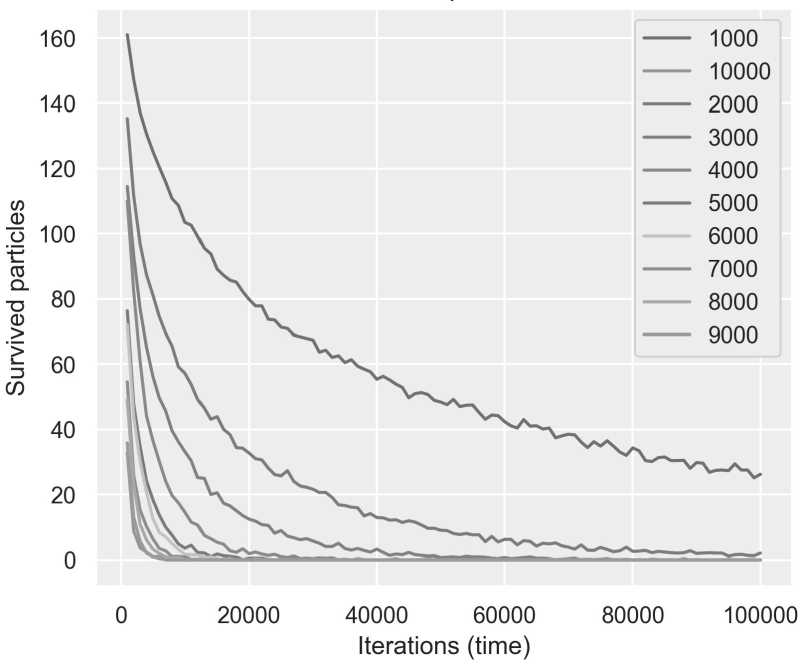
Рис. 3. Зависимость числа выживших части от времени (итераций) при различных числах ловушек. Линии соответствуют различным количеству ловушек

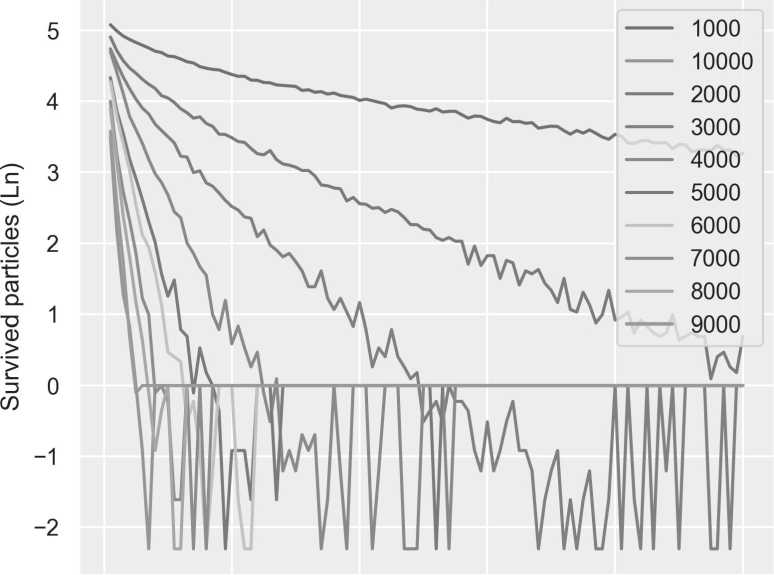
Очевидно, что зависимость от времени носит экспоненциально убывающий характер, поэтому для наглядности будем использовать логарифмическую шкалу см. рис. 2.

О 20000     40000     60000     80000     100000

Iterations (time)

Рис. 4. Зависимость логарифма числа выживших части от времени (числа итераций) при различных числах ловушек

Линии различных цветов соответствуют различным числам ловушек от 1000 до 9000.

Из рис. 4 видно сильное флуктуационное поведение исследуемых зависимостей на больших временах. В настоящей статье будет исследовано именно это поведение на больших временах. Оказывается, что на больших временах это поведение носит ступенчатый характер — см. рис. 5.

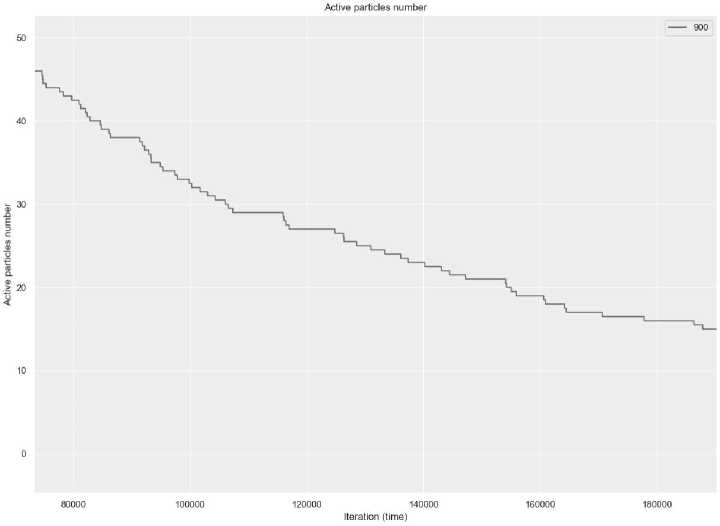
Рис. 5. Ступенчатая зависимость числа выживших частиц на больших временах при числе ловушек N=9000

Таким образом, впервые путем численного моделирования на больших временах было обнаружено ступенчатое поведение (при этом, чем меньше ловушек изначально в конфигурации, тем более это ступенчатое поведение выделяется). Более подробно это поведение будет исследовано в последующих пунктах.

2.2    Ступенчатые функции для усреднённых данных

Здесь и далее под ступенчатой функцией будет пониматься интервал, на котором число активных частиц постоянно, длиной функции будем считать число итераций на котором число активных частиц было постоянным (ввиду дискретности данных будем брать разность между началом и концом интервала). Для поиска ступенчатых функций разработан алгоритм, который анализирует файл с данными и составляет отчетный файл с информацией вида: количество частиц; первая итерация на которой найдено значение; последняя итерация; длина функции; высота (разница в количестве частиц с предыдущим).

В качестве примера приведем гистограммы, полученные для значений «длина ступенчатой функции», по количеству активных частиц. Результаты для количества ловушек 600.

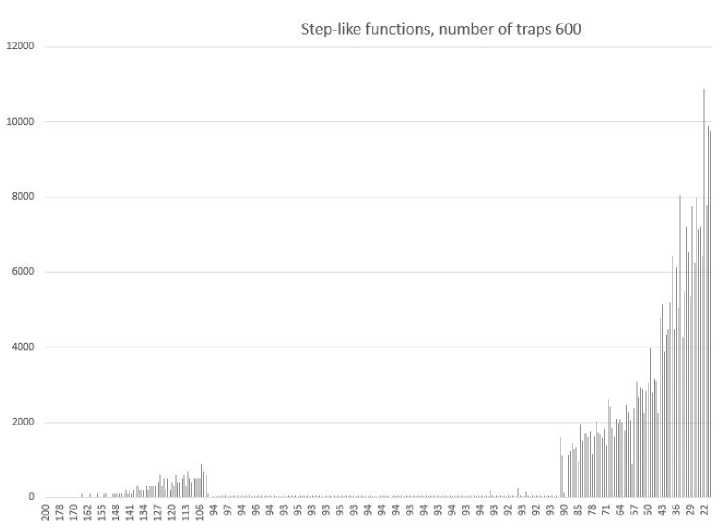
Рис. 6. Ступенчатое поведение со временем, число ловушек N = 600

На гистограммах по оси X отображено количество активных частиц (усредненное), по оси Y — длина ступенчатой функции. Или говоря по-другому — в течение какого времени (числа итераций) не меняется число активных частиц. Анализ данных конкретных запусков также подтверждает, что в течении достаточно большого количества итераций (более 200) число активных частиц остается постоянным так как нет захвата на ловушки. Это обусловлено тем, что частицы попадают в область, в которой нет ловушек. Подобные области без ловушек наблюдаются и при других количествах ловушек (М=900, 1000). Также отметим «зону» без ступенчатых функций, которая возникает при достижении числа шагов близких к числу времени захвата на ловушки значение соответствующих ступенчатых функций уменьшается.

2.3    Анализ статистики ступенчатых функций

Статистика по ступенчатым функциям приведена в таблице 1. Данные приведены для как для посева ловушек и так и числа частиц.

Таблица 1. Общие характеристики ступенчатых функций

Количество ловушек	Количество частиц	Количество функций	Максимальная длина функции
8800	2640	1403	713000.0
8800	4400	2065	349420.0
8800	8800	3441	34140.0
8800	10560	3366	46110.0
8800	13200	2824	224730.0
8800	13920	2603	398200.0
8800	14960	2371	405000.0
8800	17600	1887	360990.0
8800	22000	1319	354870.0
93200	27960	388	22010.0
93200	46600	944	58210.0
93200	93200	8215	11410.0
93200	111840	4386	182380.0
93200	139800	1366	60050.0
93200	147439	1102	76900.0
93200	158440	782	32320.0
93200	186400	436	11450.0
93200	233000	201	8220.0

Следовательно, количество ступенчатых функций для заданного посева ловушек растёт при увеличении количества частиц, максимальное количество достигается, когда число ловушек равно числу частиц, после чего количество функций уменьшается. Эта закономерность прослеживается для двух посевов ловушек.

Далее исследуем поведение ступенчатых функций. Построим график зависимости длины ступенчатых функций от количества активных частиц.

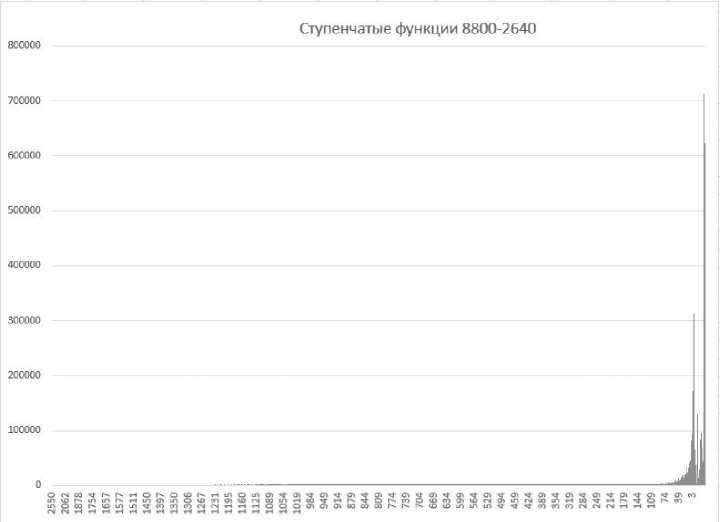
Рис. 7. Гистограмма ступенчатых функций для конфигурации (8800, 2640)

Из этого графика вытекает, что длина ступенчатой функции в зависимости от числа частиц растёт экспоненциально. Для более детального анализа разобьем график на несколько частей по длинам ступенчатых функций. Для посева ловушек N = 8800 были выбраны следующие интервалы по длинам: [0, 1000], [1000, 25000], [25000, макс]. Пример такого изображения представлен на рис. 8.

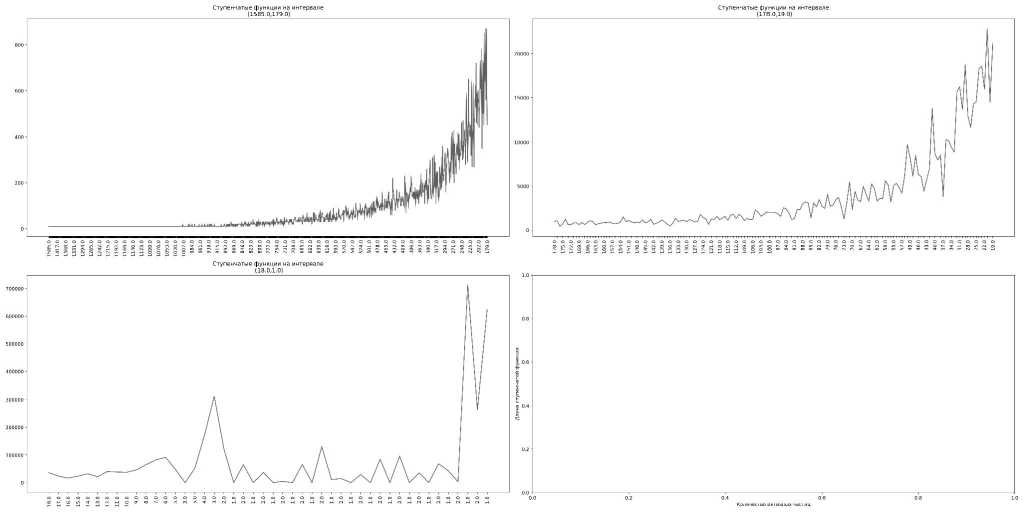
Рис. 8. Длины ступенчатых функций. Конфигурация (8 800,2640)

На рисунке по осям х — число активных частиц, по осям у — длина ступенчатой функции. Рисунки продолжают друг друга слева направо, сверху вниз.

Для конфигурации с посевом ловушек 93200 отличаются меньшим максимальным значением для длины ступенчатых функций, по этой причине были выбраны следующие интервалы: [0, 1500], [1500, макс].

2.4    Распределение ступенчатых функций

Было вычислено распределение по длинам ступенчатых функций. Для этого были выявлены ступенчатые функции ненулевой длины и посчитано их количество (для каждого значения длины). Полученный массив данных был отсортирован по возрастанию длин.

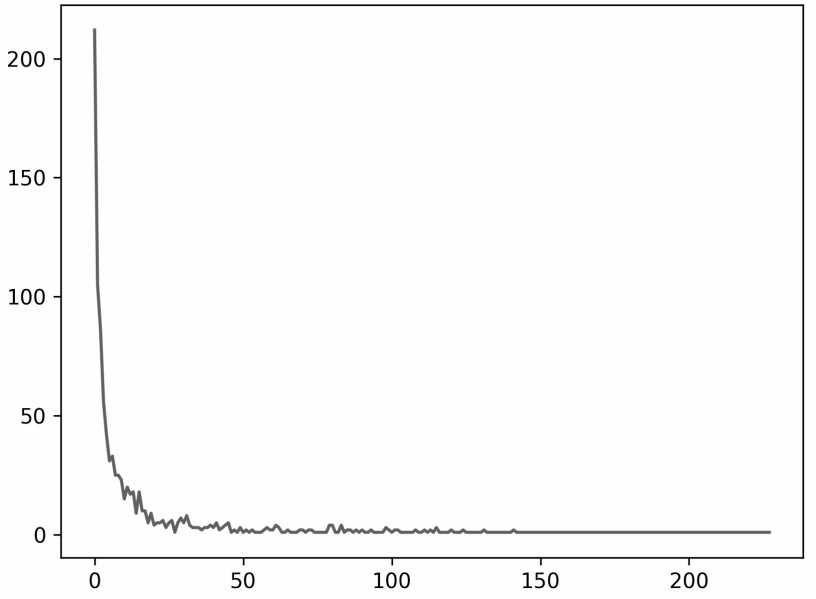
Рис. 9.1. Распределение ступенчатых функций для конфигурации (8800, 2640)

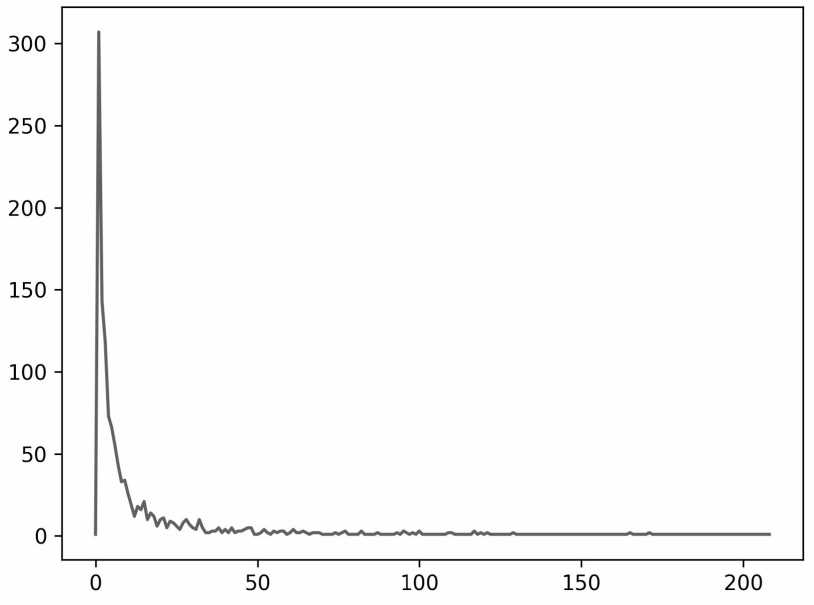
Рис. 9.2. Распределение ступенчатых функций для конфигурации (8800, 17600)

Заключение

Проведено численное моделирование захвата частиц на ловушки в цилиндрических порах. Исследованы различные поведения временных зависимостей числа активных частиц на малых временах t <<  t_c и на больших временах t_c <<  t , в качестве характерного времени выступает время захвата на ловушки t_c . Установлено быстрое экспоненциальное убывание числа активных частиц за счет захвата на ловушки, однако на асимптотически больших временах наблюдаются сильные флуктуации изменения числа активных частиц. При подробном исследовании долговременных асимптотик выживания частиц, диффундирующих в порах с ловушками, было обнаружено необычное ступенчатое поведение этих асимптотик. Этот эффект можно объяснить появлением на цилиндрической поверхности областей, свободных от ловушек и появившихся как за счет флуктуации концентрации ловушек (механизм Балагурова — Вакса), так и за счет заполнения ловушек предшествующими диффундирующими частицами, попавшими на ловушки. В случае заполнения ловушка уже не может захватить последующие частицы. Насколько нам известно, впервые обнаружено такое ступенчатое поведение в средах с ловушками. Исследована статистика этих ступенчатых функций. Получено распределение ступенчатых функций по длинам.

Интересным представляется дальнейшее исследование влияние электрического поля на захват частиц на ловушки, в том числе, и на долговременные асимптотики [11, 12].