Исследование движения большой орбитальной космической системы цепочечной структуры в гравитационном поле под действием сил светового давления

Обеспечение и поддержание заданной ориентации искусственных спутников Земли представляет собой одну из важнейших задач управления их движением. Определенная ориентация требуется как для коррекции траектории, так и для успешного выполнения своих функций спутниками связи, метеорологическими и навигационными спутниками, для проведения в космосе многих научных исследований, а также для экономии энергии спутника. В зависимости от поставленных задач ориентация искусственных спутников может осуществляться активными или пассивными методами.

Работа пассивных систем ориентации спутников основана на использовании свойств гравитационного и магнитного полей, эффекта сопротивления атмосферы и светового давления, гироскопических свойств вращающихся тел. Важное свойство пассивных систем ориентации спутников и космических систем заключается в том, что они не требуют датчиков ориентации и исполнительных элементов и могут функционировать продолжительное время, не расходуя энергию и топливо.

Для разработки пассивных систем прежде всего надо понять структуру действующих сил на орбитальную станцию и поведение системы в свободном движении.

В работе продолжаются исследования И.А. Вертипрахова и Н.А. Репьяха по динамике БОКС [1].

1. Описание системыи вывод уравнений движения

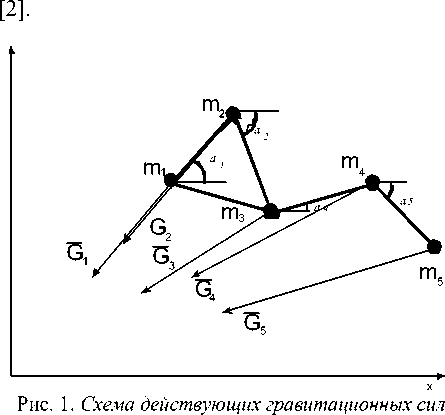
Действующие на систему внешние силы потенциальны. Это силы гравитации, действующие на материальные точки (рис. 1), расположенные на концах невесомых стержней системы, силы светового давления (рис. 2). Система имеет 5 степеней свободы, а значит, и обобщенных координат. За обобщенные координаты q_l , q^ , q ₃, q ₄, q₅ приняты: абсцисса и ордината опорной точки т_х и углы наклона стержней к оси ОХ абсолютной системы координат, центр которой совпадает с центром ньютоновского центра гравитации

Sj - функции сил светового давления.

— т.т г j зе мли j

G j = g —7— r_j

Здесь g - гравитационная постоянная,

R слл—земля

R

^ Сол — — парус J

l j cos Т j n . ,

p - солнечная постоянная, n - вектор нормали к теневой поверхности, т - угол падения света на поверхность lj [3].

Для простоты расчетов функцию тени и полутени земли вводить не будем.

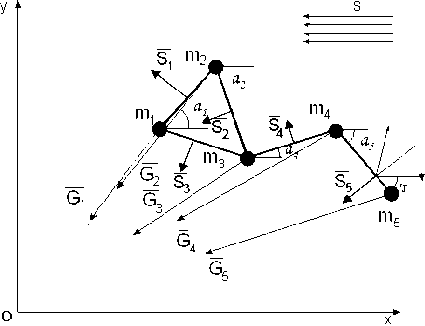
Рис. 2. Схема действующих сил

Поскольку связи, наложенные на точки, голономны, математическая модель движения системы строится в виде уравнений Лагранжа второго рода.

d д T    д T

dt

д qj

д q

д и д qi

Здесь T - кинетическая энергия системы, U -силовая функция, q_t - обобщенные координаты, q_t - обобщенные скорости.

q 1 = x , q ₂ = y , q₃ = a i , q ₄ = a ₄,q ₅ = a ₅ .

На каждую j -ю точку mj системы действует сила

F j = G + S j ,           (2)

где Gj - функции гравитационных сил,

Для построения математической модели движения БОКС рассматриваемой структуры введем неподвижную, связанную с Землей систему координат OXY и зададим обобщенные координаты системы.

Положение первой точки m будем определять с помощью координат ( x, y ). Положения остальных точек зададим углами отклонения р ( j = 1.. n ) стержней lj относительно оси OX [4].

Физическая модель имеет в данном случае 5 степеней свободы, соответственно вектор-строка обобщенных координат, описывающая положение механической системы, равна

Запишем координаты точек механической системы в абсолютной системе координат XOY [5]:

m :

m :

' x1

;

, y 2 = У 1 ⁺ l i sin ^a i^;

	5	д д x.
Q s =	z j = 1  2	+ 1 д q ,	l + 1 д q , J	+ ,       (11)
+ S j	'д x,. —l +	д L
2	1 д q i	д q, 7

m :

X = x ₂ + 1 ₂ cos a . У з = У 2 ⁺ l 2 ^{sin a} 2 ,

где

l ² + L ² - L ² где a = a + n + arccos -¹---²---—

21          2ll для треугольного элемента

S ² PR l j co'

\ R 2 7

П       1     ( П      1

--a I cos-- T : I , 2 ^j )    \ 2 ^j 7

V" v2 7

j ^,

^m 4 ^: m :

;

l У 4 = У 3 + 1 4 sin a ₄

x = X 4+ 1 ₅ cos a ^;

т j - угол падения света на парус l j , p – солнечная постоянная для Земли, R – расстояние Солнце – Земля, R – расстояние Солнце – Парус.

Из равенств (5) определяются скорости

v j = J + L

точек системы и значение кинетической энергии T системы

T = Z

J = 1

m j v ² j

где v – абсолютная скорость точки m .

Частная производная T по обобщенным координатам примет вид

d T _ Л m j д x j ²   д у j ²

^д q i   J = 1 ^{2    д} q i ^{+ д} q i

Обобщенные силы Q в обобщенных координатах:

Qt = Qg, + Q s , ,

где

—*

z—

J = 1

[4 ₊ M, ₂ ^д q i    ^d q i )

m M r

3, 22

( r – радиус-вектор точки m )

В результате математических преобразований получим уравнения (12) движения системы [5]:

d x

I = d VmL ^L i dl       2   дq,

m

д X

—

—

2    5 q,

^д q ,

5 mj_ д х_ ^z T r q

j = 1

—

^д q ,

—Z(—g)

^j = 1       XX ² + У ²

J q i   ^д q i

—

f S xj д хX % 2 <д q i

—^L +

дx^ , ^

дqi 7

—

S

+ _ L   +

^д У

² ^ ^д q i

^д q i 7

( i = 1, 2,…, 5).

2. Исследование движения 5-массовой БОКС

Исследование поведения системы проводилось на модели, состоящей из пяти тел, принимаемых за материальные точки. Определяющими параметрами системы являются массы тел, длины стержней и начальные условия. Орбитальное движение системы m₁ , m ₂,..., m₅ зададим движением первой точки, предполагая, что в начальный момент она находится на расстоянии R земли + h от гравитационного центра и имеет начальную скорость, соответствующую круговой скорости для этого расстояния:

_  yM v0   V R - h ’ где R - радиус земли, h - начальная высота точки m{ над поверхностью Земли [5].

Начальное состояние системы полностью определяется размером БОКС и положением точек m_x , m ₂,..., m₅ в начальный момент времени. Предполагается, что в начальный момент времени t система движется согласно условиям (13), паруса lj полностью отражают световой поток.

Ниже приводится анализ движения 2 БОКС из пяти точек:

• I    - в поле гравитационных сил,

• II    - в поле сил гравитации и светового давления, соединенных последовательно, с образованием треугольника в точках { m_x , m₂ , m₃ } в транспортирующей системе координат m^y (рис. 3, 4, 5, 6, 7), при этом массы всех тел одинаковы и равны m = 60 кг , длины стержней { l , / ₂, / ₃, / ₄, / ₅} = {500, 600,

  700, 1000, 1500} м соответственно, начальные углы и их угловые скорости равны:

а = 0, а = 0, а = 0, а = 0,    (13)

а = 0.01, а = 0.01, (Z₄ = 0.01, (Z₅ = 0.01.

В начальный момент времени системы изображены на рис. 3.

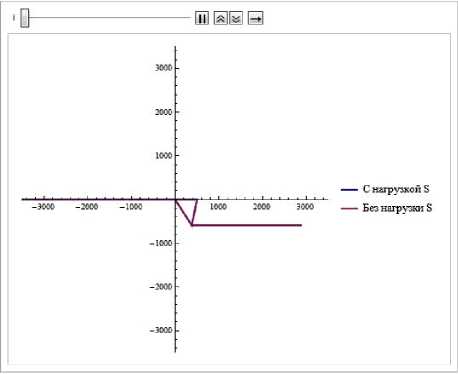
Рис. 3 . Системы в начальный момент времени 1 ₀

На первом этапе движения системы к моменту t 1 (рис. 4) за счет гравитационного поля происходит смещение положения "хвоста". Так как система с учетом S₂ располагается практически параллельно к действию силы светового давления - системы не сильно различаются своей ориентацией.

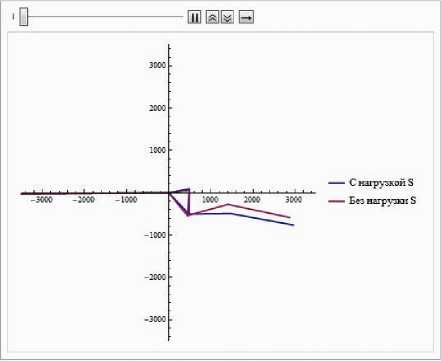
Рис. 4. Системы в момент времени t^ =60 c

К моменту времени t (рис. 5) наблюдается ускорение вращения модели без учета сил светового давления. Модель с учетом Sj наоборот замедляет свое вращение за счет действия сил давления на "хвостовые" паруса.

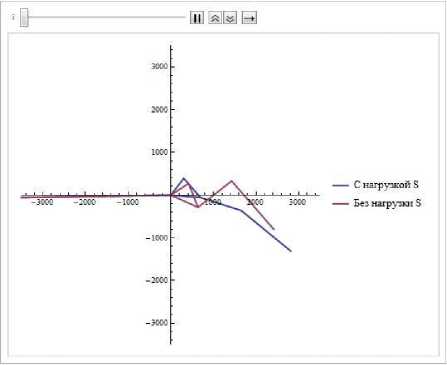
Рис. 5. Системы в момент времени t₂ =120 c

С увеличением угла наклона к световому потоку возрастает действие сил светового давления, вследствие чего "хвостовые" паруса начинают ускоряться, придавая противоположное вращение системы с парусами (рис. 6).

К моменту времени t = 240 с система с парусами приобретает хаотическое движение за счет увеличения импульса сил S . Система без парусов приобретает вращение против часовой стрелки. Система с парусами приобретает двойное вращение, вращение 3 звеньев против часовой стрелки и вращение "хвоста" по часовой стрелке (рис. 7).

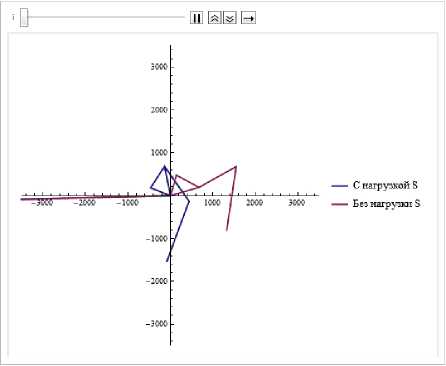
Рис. 6. Системы в момент времени t =180 c

Через некоторое время движение системы с парусами будет приобретать все более хаотический характер.

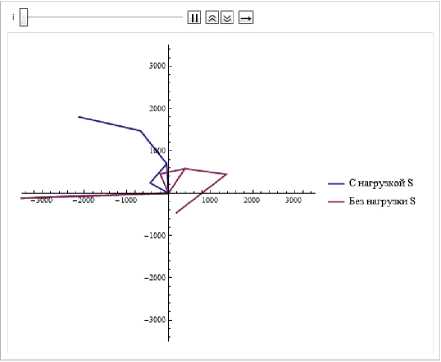
Рис. 7. Системы в момент времени t =240 c

Заключение

Данные модели движения описывают действие сил G и S на БОКС. Для дальнейшего развития модели динамики БОКС необходимо вводить массы стержней или парусов, учитывать функцию тени как от источника гравитации, так и от самих парусов. Также необходимо учесть и действие возмущающих факторов (например, притяжение Луны и Солнца, реликтовые излучения, электромагнитные излучения).

Исследование движения 5-массовой системы проводилось численно с применением пакета Wolfram Mathematica 9.01 в предположении равных масс точек, начального поступательного состояния системы в плоском центральном гравитационном поле c полным отражением светового потока. Приведено описание последовательных состояний системы в транспортирующей системе координат для двух моделей на промежутке одного оборота системы вокруг опорной точки m .

Создана визуализация движения 5-массовой системы в свободном вращении вокруг источника гравитации c действием сил светового давления.