Исследование линейной устойчивости адвективного течения во вращающемся горизонтальном слое жидкости с твердыми границами методом дифференциальной прогонки

Одной из важнейших задач гидродинамики является исследование устойчивости конвективных и адвективных течений жидкости, которые могут быть описаны аналитически [1, 2]. Широкое распространение в задачах устойчивости конвективных и адвективных течений получили метод Галёркина, метод пошагового интегрирования с ортогонализацией, метод дифференциальной прогонки и метод сеток. В первых трех случаях задача устойчивости сводится к многократному решению краевой задачи для обыкновенных дифференциальных уравнений. В последнем случае решается краевая задача для одномерной системы уравнений в частных производных.

Адвективное течение, возникающее в плоском горизонтальном слое жидкости при отсутствии вращения для случая, когда температура на обеих границах линейно изменяется с продольной координатой, было впер-

вые описано Р.В.Бирихом аналитически [3]. Особенностью такого течения является отсутствие вертикальной компоненты скорости, вектор скорости в потоке здесь ориентирован перпендикулярно силе плавучести, которая является основной причиной движения. Устойчивость таких течений, возникающих в горизонтальном слое жидкости при отсутствии вращения, исследовалась в основном методом дифференциальной прогонки и изучена достаточно подробно в работах В.М.Мыз-никова совместно с другими авторами [1].

Адвективное течение, возникающее во вращающемся плоском горизонтальном слое жидкости, для случая, когда температура на границах линейно изменяется с продольной координатой, было впервые выведено аналитически С.Н.Аристовым [4]. Как и в случае без вращения, у адвективного течения отсутствует вертикальная компонента скорости, вектор скорости в потоке ориентирован перпендикулярно силе плавучести, однако имеются обе горизонтальные компоненты векто- ра скорости. Устойчивость адвективного течения, возникающего во вращающемся горизонтальном слое жидкости, исследовалась К.Г.Шварцем с использованием метода сеток в работах [5, 6].

В данной работе исследуется устойчивость адвективного течения во вращающемся слое жидкости с малым числом Прандтля ( Pr = 0.1) методом дифференциальной прогонки. Результаты сравниваются с результатами, полученными методом сеток в работе [7].

• 1.    Постановка задачи

Рассмотрим плоский горизонтальный слой несжимаемой жидкости, ограниченный твёрдыми плоскостями z = ±h и вращающийся с постоянной угловой скоростью Q = Q 0 iz, где iz – орт-вектор вертикальной осиz . На- правление оси вращения совпадает с вертикальной осью координат. Изучение адвективных течений будем производить на основе уравнений конвекции в приближении Буссинеска во вращающейся системе отсчета в декартовой системе координат [1]. Выбрав в качестве единиц измерения длины, времени, скорости, температуры и давления соответственно h, h2 V, g^Ah 2 V, Ah, p0 g^Ah2 (здесь v - коэффициент вязкости, g - ускорение силы тяжести, в — коэффициент теплового расширения, A – постоянный горизонтальный температурный градиент на границе слоя, р0 - средняя плотность), мы получим исходные уравнения в безразмерном виде [5]:

V+ + Gr(vVv)+ Tail (iz x v)= div v = 0,

-V p + A v + T • i_z,

— + Gr (vV T )= — A T, d t             Pr где v – вектор скорости, T – температура, p - давление, Gr = geAh 4 V 2 — число Грасгофа, Ta = (2Q0h2 V)2 - число Тейлора, Pr = VX -число Прандтля. Здесь % - коэффициент температуропроводности. На обеих плоскостях задана температура, линейно меняющаяся с продольной координатой x , условия прилипания и замкнутости потока z = ±1: T = x, v = 0, Jvxdz = 0, Jvydz = 0. (2)

-i                -i

Профили скорости и температуры возникающего адвективного течения описываются в виде точного решения задачи (1)–(2) [5]

u 0 ^{( z} ) = ^Im f i ⁽ z ) ,

Ta v 0 (z ) =      (z - Re fi(z )\

Ta w0 (z) = 0, T0 = x + GrPrr0 (z),            (3)

^T 0 ^{( z} ) =       ^v 0 ^{( z} )

Ta f1 (z )=~h$ ■ *=4/r(1+i i=7"1 ■ где u 0 (z), v0 (z) и w 0 (z) - компоненты вектора скорости, Re – действительная часть комплексного значения, Im – мнимая часть комплексного значения.

Для исследования устойчивости стационарного плоскопараллельного адвективного течения применим метод малых возмущений [1]. Рассмотрим возмущенное течение v = v 0 + V , T = T 0 + 0 , p = p 0 + P , где V , 0 , P – малые нестационарные возмущения. Пренебрегаем квадратичными по V = ( u , v , w ) и 0 слагаемыми и получаем

I v + Gr (( V V^ + ( v 0 V V ) + TP ( i z x V ) = = -V P + J V + 0 • i z ,                   ₍₄₎

div V = 0,

• — + Gr ( V v T_o + V o ) = — A0 .

• 2.    Анализ результатов

dt      \    °    ° j _pr

На твердых границах слоя возмущения скорости обращаются в нуль. Кроме того, будем считать, что ограничивающие слой пластины являются идеально теплопроводными; практически это означает, что теплопроводность материала, из которого изготовлены пластины, много больше теплопроводности жидкости. Отсюда следует, что на границах исчезают возмущения температуры. Имеем, таким образом, граничные условия для возмущений z = ±1: V = 0, 0 = 0.           (5)

В силу большой сложности исследования устойчивости течения в трехмерной постановке будем рассматривать предельный случай – пространственные винтовые периодические по x возмущения в виде валов с осью, перпендикулярной оси Ox при Pr = 0.1 в случае возмущений гидродинамического типа.

Учитывая дивергентность возмущений скорости, введем функцию тока возмуще-дщ      дщ ний щ : и =---, w =--и вихря возму- дz         дx д 2щ  д2щ щения скорости щ = —— +--— = А щ . В каче-дxz   дz2

стве малых возмущений рассматриваем нормальные возмущения вида tf ( t, x, z) = tf (z )exp (- At + ikxx), щ(t, x, z) = щ (z )exp (- At + ikxx), v (t, x, z) = v1 (z )exp (- At + ikxx), 3(t, x, z) = 31 (z )exp (- At + ikxx).

Проводились тестовые расчёты для случая отсутствия вращения, которые полностью совпали с результатами работы Мызни-кова [1, 9].

Анализ устойчивости производился для случаев очень слабого вращения (0 <  Ta <  0.1), слабого вращения (0.1 <  Ta <  10²), умеренного вращения (10² <  Ta <  10³) и быстрого вращения (10³ <  Ta <  2 •Ю⁴). При всех значениях числа Тейлора наблюдался монотонный характер неустойчивости, мнимая часть декремента A равнялась нулю.

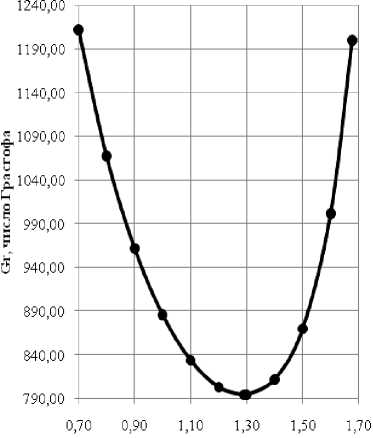
Для значений числа Тейлора, близких к нулю, минимальное критическое значение числа Грасгофа ( Gr ) достигается при k_x = 1,29 . На рис. 1 представлена нейтральная кривая при Ta = 10 ^{— 12}, Gr_k = 794,12 .

Здесь tf 1 ( z ) , щ 1 ( z ) , v 1 ( z ) , 3 1 ( z ) - амплитуды возмущений, A - декремент возмущений, k_x

– вещественное волновое число, характеризующее периодичность возмущений вдоль

направления x .

Подставляя (6) в (4) и избавляясь от давления, получаем систему обыкновенных дифференциальных уравнений вида

tf = tf^    ( i = 1,2,3,5,7),

^ 4 = ⁽ 2 kx + ik_xGr • u о

—

^{+ (— k}4 ^{— ik}x^{Gr ( k}2 u 0 ⁺ u 0 + ^{( —} Ta a ^tf + ik xw.

) ^ 3 ⁺

) + kx a)^1 +

tf 6 = JP a (p + + ( — k x Gr • v 0 ) tf i +

^{+ ( k}x ^{2 + ik}x^Gr • u 0 ^{— A} ) tf 5 , tf ‘ = GrPr tf + ( — k_xGr ² Pr T ’ tf +

+ ( k ² + ik_xGr • u ₀ — A Pr ) ^₇

kT> волновое число

Рис. 1. Нейтральная кривая при очень слабом вращении (Ta=10^-12)

с граничными условиями (5) в виде z = ±1: tf! = ^2 = tf5 = tf = 0- (9) Здесь tfi = Щ1, tf2 = щ‘, tf, = Щ1 , tf = щЦ1, tf5 = V1, tf6 = v1, tf ■ = 31, tf8 = 3'1 .

Краевая задача (8)–(9) решалась методом дифференциальной прогонки с помощью пакета прикладных программ "Гидродинамическая устойчивость" [8].

При слабом вращении основные расчеты проводились при Ta = 1 . Результаты показали, что минимальное критическое значение числа Грасгофа достигается при k_x = 1,28 . Критические значения числа Грасгофа, вычисленные с различной точностью интегрирования, представлены в табл. 1.

Таблица 1. Gr для различной точности интегрирования при слабом вращении

ε	Gr	δ
10 -1	810,28	1,29%
10 -2	817,81	0,36%
10 -3	820,25	0,06%
10 - 4	820,50	0,03%
10 -5	820,52	0,0280%
10 -6	820,523	0,0276%

Оптимальная точность интегрирования порядка 10 ^{- 4} , так как разница с результатами более высокой точности невелика, а экономия времени, по сравнению с решением, полученным при большей точности, очень существенна. Разница между результатами работы [5] составляет менее 0,03%. Время работы программы при вычислении критического числа Грасгофа с различной точностью интегрирования при k = 1,28 представлено в табл. 2.

Таблица 2. Время работы программы при различной точности интегрирования

ε	10 -4	10 -5	10 -6
Время работы программы	7 с.	74 с.	768 с.

С ростом числа Тейлора критическое число Грасгофа растет, вращение стабилизирует адвективные течения.

При умеренном вращении устойчивость течения снижается. Основные расчеты проводились при Ta = 500 . Критическое значение числа Грасгофа достигается при k = 0,99 . Критические значения числа Грасгофа, вычисленные с различной точностью интегрирования, представлены в табл. 3.

Таблица 3. Gr для различной точности интегрирования при умеренном вращении

ε	Gr	δ
10 -1	1527,86	5,92%
10 - 2	1439,91	0,17%
10 -3	1437,73	0,19%
10 -4	1437.40	0,0035%
10 -5	1437.37	0,0055%
10 -6	1437.365	0,0059%

Разница между результатами работы [5] составляет менее 0,006%. В этом случае нейтральная кривая имеет специфическую форму "носика" (см. рис. 2).

При быстром вращении основные расчёты проводились при Ta = 20000 . Критическое значение числа Грасгофа ( Gr = 12055 ,25 ) достигается при k = 3,7 . Разница между расчетами, полученными методом дифференциальной прогонки и методом сеток, также составляла менее 0,006%. С ростом числа Тейлора вращение стабилизирует адвективное течение.

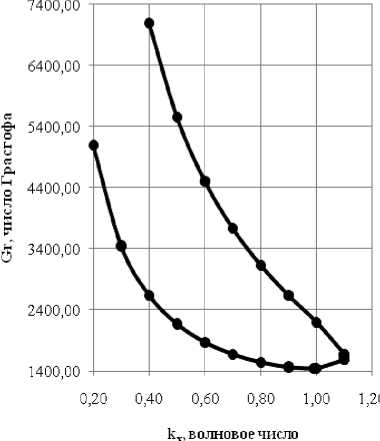
Рис. 2. Нейтральная кривая при умеренном вращении (Ta=500)

Заключение

Расчеты показали, что вращение не меняет монотонный характер адвективного течения для всего рассматриваемого диапазона чисел Тейлора. Результаты, полученные методом дифференциальной прогонки, согласуются с результатами работы [5], что свидетельствует о работоспособности разработанного алгоритма и возможности его дальнейшего применении.