Исследование математической модели конфликтов в группе роботов
Автор: Попов Н.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (32), 2016 года.
Бесплатный доступ
Представлен вывод достаточного для бесконфликтности двух роботов условия; полученный признак исследован на применимость. Изучены условия, при которых на заданных тактах наступит конфликт между роботами. Приведена оценка максимального числа парных конфликтов в группе роботов.
Роботы, эмоции, конфликты, исследование, математическое моделирование
Короткий адрес: https://sciup.org/14730151
IDR: 14730151 | УДК: 519.711.2
Текст научной статьи Исследование математической модели конфликтов в группе роботов
В теории эмоциональных роботов [2, 5] вводится понятие эмоционального воспитания робота, которое определяется следующей формулой:
R + 1 = Ь- R + r + i
R 1 = r 1 .
Здесь i – такт – отрезок времени, в течение которого робот испытывает некоторую эмоцию. Значение ri характеризует эффект, вы- званный данной эмоцией, и называется элементарным воспитанием. Величина Ri описывает общее состояние робота после i воспитательных тактов и именуется суммарным воспитанием. Коэффициенты памяти 0 < 0i < 1 характеризуют тенденцию суммарного воспитания прийти к нейтральному состоянию (R = 0) в отсутствие воспитательных воздействий.
В работе [3] исследуется случай равномерно забывчивого робота [2, 5], коэффициенты памяти которого неизменны, т.е. 0i = 0 = const. Для данного случая устанавливается критерий сходимости суммарного воспитания. Согласно данному критерию, сходимость последовательности {Ri}, опре деленной соотношением (1), эквивалентна сходимости последовательности элементарных воспитаний {ri}.
Введем в рассмотрение двух роботов σ 1 , σ 2 , характеризующихся своими суммарными воспитаниями R i [ с 1 ] , R j [ с 2 ] . Согласно основному труду по теории роботов [2], конфликт между двумя роботами наступит тогда и только тогда, когда они имеют противоположные воспитания. То есть Ri [ с 1 ] = - R j [ с 2 ] или R i [ с 1 ] + R j [ с 2 ] = 0 .
Целью настоящей статьи является изучение математической модели конфликта двух роботов.
Пусть у нас есть два равномерно забывчивых робота σ 1 , σ 2 , имеющих коэффициенты памяти соответственно 0 1 , 0 2 (0 < 0 1 , 0 2 < 1). На роботов воздействуют при помощи равноценных эмоций – таких эмоций, эффект от которых одинаков [2, 5] r i = r = const . Обозначим вызванные у роботов σ 1 , σ 2 эмоциональные отклики как r 1 , - r 2 , при этом r 1 , r 2 > 0 .
Суммарное воспитание, полученное первым роботом в ходе воспитательного процесса, состоящего из i тактов, выразится через соотношения:
R i \ h 1 ] = 0 1 • ^-1 Ь ] + r i , R i h ] = r 1 .
Справедлива следующая цепочка:
Л‘ + 1) > /(i) « г ■ ——— > г
1
о oi+1 < 0i о 0 < 1.
1 - о1
Аналогично и для второго робота:
R ; \ h 2 ] = 0 2 • R j - 1 \ h 2 ] - r 2 , R i k 2 ] = - r 2 .
При наложенных условиях R i \ h 1 ] и R j \ h 2 ] допускают явные решения в виде
^ilcj = fi + Ti ■ 0] + ■■■ + ?! ■ di ■ или
Таким образом, последовательность { f ( i )} действительно оказывается возрастающей при данных условиях.
Лемма 2
Если r > 0 и 0 < в < 1 , то
„ 1 - 0‘ г .
r --<---- для любого i .
1 - в 1 - в
R i l ^ X ] = r 1 •
RjW = -*z - гг ■ % или
1 - o i
1 - 0 1 ;
, — rz ' ®j
Доказательство
Истинность леммы прямо следует из цепочки
г- < «1 О’ < 1 « О1 > 0 ^
о в > 0.
R j \ h 2 ] = - r 2 •
1 - 0 2
1 - 0 2
.
Теорема 1
Пусть r1, r2 > 0 . Если коэффициенты памяти 01 , в2 ( 0 < в1,в2 < 1 ) удовлетворяют одному из неравенств:
Условие наступления конфликта для пары роботов σ 1 , σ 2 , у каждого из которых воспитательный процесс занял i и j тактов соответственно, запишется в виде:
R i ^ ]= - R j \ h 2 ]
0 1 + r-r
---r— < 0
1 - 0 1 2
или
r 1
1 - e {
—
1 - 0 1
= r2
1 - 0 2 j •-----------------------
.
1 - 0 2
Коэффициенты памяти θ 1 , θ 2 , при которых равенство (2) не может быть выполнено ни при каких i и j ( i , j > 2 ), если r1 и r2 заданы, называются антиконфликтными коэффициентами памяти [2]. Если коэффициенты памяти двух роботов антиконфликтные, то роботы никогда не окажутся в состоянии конфликта.
Итак, каким соотношением должны быть связаны коэффициенты памяти θ 1 , θ 2 , чтобы являться антиконфликтными?
Лемма 1
или
0 1 + r-r
---— > в , 1 + 0 1 2
то равенство (2) не может быть ни при каких i, j > 2.
выполнено
r1 •
Доказательство
Используя лемму 2,
10 < Л_ для i > 2 .
1 - 0 1 1 - 0 1
По лемме 1
2 i-e3 для j > 2 .
Если
r 1
1 - 0 1
получаем
12^ i-e3
< r 2 • ( 1 + в2 ) , то справедлива
При r > 0 и 0 < в < 1 последователь-
1 - 0 „ ность f (i) = r • ——— является возрастающей.
следующая цепочка неравенств:
4 ■ ^-^ < — < r2 ■ (1 + 0,) < r2 ■ ^^
.
Доказательство:
Из нее следует невозможность выполнения равенства (2) ни при каких i и j ( i , j > 2 ).
Применяя лемму 1 к Ri [а1 ], лемму 2 к - Rj [а 2 ] и повторяя те же рассуждения, по- лучаем второе неравенство:
r 2
1 - 0 2
< Г . ' ( 1 + 0 1 ).
Полученные неравенства легко преобразуются к виду (3), (4).
Таким образом, выполнение любого неравенства из условий теоремы 1 влечет за собой вывод, что коэффициенты памяти θ 1 , θ 2 – антиконфликтные.
Проанализируем полученный результат. Всегда ли по полученным неравенствам можно определить пару чисел, являющихся анти-конфликтными коэффициентами памяти? То есть, действительно ли при произвольных значениях r1, r2 > 0 найдутся такие коэффи- циенты памяти θ1 , θ2 , которые удовлетворяли хотя бы одному неравенству (3) или (4)?
Теорема 2
Для любых r 1 , r2 > 0 существуют такие числа ( 0 < 0 1 ,0 2 < 1 ), которые удовлетворяют хотя бы одному неравенству ( 3 ) или ( 4 ).
Доказательство
Допустим обратное. Тогда найдутся такие числа r 1 и r 2 , что ни одно из неравенств (3) и (4) не может быть выполнено, какие бы числа θ 1 , θ 2 ни взять. В этом случае, при произвольных значениях θ 1 , θ 2 , справедливо двойное неравенство:
ех+^ ех+^
----3— > 02 >---^“ (5)
. (5)
Поскольку 0 < 02 < 1, должны выпол- няться следующие условия:
Система (6) следует из того, что если при некотором значении θ 1 было бы, например ,
01+ '^ r ц = 2— < 1, то мы могли бы взять в
1 - 0 1 ’
(1 1 + ц ^
качестве 0 = max I , I и тем самым
2 12 2 J найти числа θ1 , θ2 , при которых двойное неравенство (5) не выполняется.
После некоторых преобразований получаем эквивалентную системе (6) систему
r^> 2'(1 - 0)
V . (6')
I <1+01
Ввиду того, что левые и правые части неравенств системы (6') положительны, эти неравенства можно почленно перемножить:
r/ r2 2
> 2 .(1 - 01 )
r 2 r 1
или
1 > 2 - ( 1 - 0 12 ) . (7)
Будучи следствием системы (6), неравенство (7) должно выполняться при любых θ1 . Но, непосредственной подстановкой видно, что, 1
например, значение 01 = — не удовлетворяет ему: 1 > — . Получили противоречие.
Таким образом, какие бы элементарные воспитания r 1 и - r 2 ( r 1, r 2 > 0 ) ни взять, можно так сконструировать двух роботов σ 1 , σ 2 , что они никогда в процессе своего воспитания (для тактов i , j > 2 ) не вступят в конфликт.
При r = r 2 неравенства (3) и (4) принимают наиболее простой вид:
01 + V r2
1 - 0 1
0 1 + r-r2 r 1
1 + 0 1
> 1
< 0
θ
—1— < 0, или
1 - 0 1 2
-°_ > 02.
1 + 0 1 2
В монографии [2] доказывается, что коэффициенты памяти 0 1 = —, 0 2 = — являются
антиконфликтными при условии r 1 = r2 . В то же время эти коэффициенты удовлетворяют
1 — 0n
Нижняя оценка для r --следует из
1 — 0
второму неравенству:
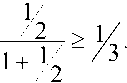
следующей цепочки:
1-0"
1-9"
Для того же случая r 1 = r 2 = r коэффи-
циенты памяти 0. = , 0 = — не будут яв-
1 2 2 4
ляться антиконфликтными, так как конфликт между роботами наступит на третьем и втором воспитательных тактах соответственно:
Последнее неравенство в цепочке справедливо, так как последовательность 0 n } является убывающей при данных условиях.
Верхнюю оценку докажем по индукции. База n = 2:
1 -
r •
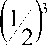
r •
-
-
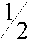
r • —
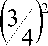
-
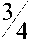
7 r • .
Легко видеть, что данные коэффициенты па-
мяти не удовлетворяют ни одному неравенст-
ву (3), (4):
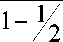
= 1 >
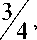
Последнее неравенство истинно, поскольку 0 < 0 < 1.
Пусть лемма выполнена для n = k . То
1 — 0к есть, r --< r • к .
’
Имеем 0к < 1 (по условию, 0 < 0 < 1 ).
Отсюда следует r • 0к < r. Складывая почленно имеющиеся неравенства, получаем: 1-6*.
г--+ r-0k
1 - 6t+1 ,.
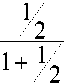
= <
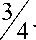
1-0
Лемма доказана.
В этом параграфе рассмотрим условия, при которых процесс воспитания двух роботов σ 1 , σ 2 приведет к конфликту между ними на тактах с номерами i и j . Как и прежде, на каждом такте элементарные воздействия на роботов – величины противоположных знаков r 1 и — r 2 . Коэффициенты памяти у роботов 0 1 , 0 2 подчиняются требованию 0 < 0 1 , 0 2 < 1 . Начальные моменты воспитания не рассматриваются: i > 2 и j > 2 .
Пусть r > 0 , 0 < 0 < 1 и n > 2 - нату- 1 — 0 n „ ральное число. Тогда r < r • ——— < r • n .
Доказательство
Теорема 3
Если r 1 , r 2 > 0 и i, j > 2 - заданные номера тактов, то коэффициенты памяти θ 1 , θ 2 , удовлетворяющие равенству (2), существуют тогда и только тогда, когда вы-
полняется система неравенств:
<
i • r > r2
. j • r2 > r1
Доказательство
Необходимость
Пусть существуют такие θ 1 , θ 2 , для ко-
1 — 0 торых r • -—= r 2
1 — 0 2
• 1 — 0 2
= 0.
Ввиду доказанной леммы, имеем i • r1 > о > r1. С другой стороны, применяя ту
же лемму, получаем j • r 2 > о > r 2 . Из сопоставления этих соотношений следует, что одновременно выполняются неравенства i • r > r 2 и j • r 2 > r 1 .
Достаточность
Пусть выполняется система (8).
Рассмотрим полиномиальные относительно θ 1 , θ 2 функции, определяющие суммарное воспитание двух роботов σ 1 , σ 2 по прошествии i, j тактов соответственно:
^И = Гх + Гх-^+'-'+Гх-е! 1
.
Расширим их область определения: 0 < 0 1 , 0 2 < 1 .
Данные функции, определенные на отрезке, являются на нем непрерывными. А значит, к ним применима теорема Больцано–Коши о промежуточном значении [4].
На концах отрезка эти функции принимают следующие значения:
Rh ]( 0 ) = r i ,- , Rfo ]( 1 ) = ■ • r i ;
— Rj [ст2 ](0) = r2, , — Rj [ст2 ](1) = j • r2.
Определим числа д = min ( i • r 1 , j • r2 ) , Д = max ( r 1 , r2 ) . Покажем, что Д > д .
i • r 1 > r 2 (гипотеза), i • r 1 > r 1 ( i > 2 ). Следовательно, i • r 1 > max ( r 1 , r 2 ) = д .
Аналогично, j • r2 > Д ( j > 2 ). Сопоставляя полученные неравенства, заключаем, что Д = min ( i • r 1 , j • r 2 ) > Д .
Исходя из самого определения чисел µ , µ , видно, что
Rih](1)> Д и — Rj[ta2](1)> Д, Д > Ri [ст1 ](0) и Д > -Rj [ст2 ](0).
Теперь, если взять произвольное число p , такое, что д < p < Д (такое число най
д + Д дется, например, p = —), то, в силу тео ремы Больцано-Коши [4], при некоторых 0'1, 02 будет Д.[о-1 ]°1')= p = -Rj [ст2 ](02), причем 0 < 0[, 0'2 < 1, поскольку p заведомо отлично от значений, которые функции R. [ст1 ], - Rj [ст 2 ] принимают на концах отрезка [0; 1].
Иными словами, удовлетворение системы (8) действительно оказывается достаточным для того, чтобы на заданных тактах i и j мог наступить конфликт между роботами.
Цель настоящего параграфа – определение максимально возможного числа попарных конфликтов в некоторой группе, состоящей из n роботов. Роботы σ 1 , σ 2 , …, σn рассматриваются в статике: воспитания каждого робота из группы (обозначим их ρ 1 , ρ 2 , …, ρn ) предполагаются постоянными величинами, отличными от нуля.
Теорема 4
Максимальное число парных конфликтов в группе из n роботов не превосхо- дит
( [ x ] - целая часть от числа x ) .
Доказательство
Условие конфликта между роботами σi и ст j запишется в виде p . + p j = 0 .
Отсюда ясно, что конфликтовать могут только роботы, у которых воспитания имеют разные знаки. Обозначим за k – количество положительных чисел среди набора { p . } . Поскольку в группе нет роботов с нулевым воспитанием, количество отрицательных выразится как n - k .
Для заданного числа положительно воспитанных роботов в группе максимальное число конфликтующих пар будет составлять (по комбинаторному правилу умножения, [1]) Mk = ( n - k ) • k (это достигается, например, если модули всех ρi равны между собой).
Отвлекаясь от натуральных чисел, с которыми имеем дело в комбинаторике, рассмотрим функцию y = ( n — x ) • x для вещественных значений аргумента x . Производная y' = n - 2 x обращается в нуль, а функция y достигает
n
максимального значения при x = — .
Если n = 2 m , то при k = — = m количество конфликтующих пар достигает своего наибольшего значения M = m 2 .
Если n = 2m +1, то, учитывая, что при nn x < — функция возрастает, а при x > — - убывает, и что y (m) = y (m +1), получаем, что максимальное число конфликтующих пар – M = m • (m +1).
В каждом из случаев выразим наибольшее число парных конфликтов через n – число роботов в группе:
2 n
-
1) n = 2 m . В этом случае M = — .
А 1 П
-
2) n = 2 m + 1 ^ m = ^ . M принима-
- n -1 n +1 n21
ет значение---== —
2 2 4 44
Объединяя случаи 1 и 2, в итоге получаем, что максимальное число конфликтующих пар в группе из n роботов составляет
(целая часть от натурального числа – само натуральное число).
В данной статье были рассмотрены парные конфликты роботов. В результате наших исследований были выявлены: метод, с помощью которого можно находить антикон-фликтные коэффициенты памяти; критерий возможности открытого конфликта при заданных тактах воспитательного процесса; оценка максимально возможного числа парных конфликтов в некоторой группе роботов.
Данные результаты можно использовать при моделировании психологического поведения группы роботов, выбирая оптимальные характеристики с целью предупреждения возможных конфликтов.
-
1. Андерсон Дж. Дискретная математика и комбинаторика. М.: Вильямс, 2004. 960 с;
-
2. Пенский О.Г., Черников К.В. Основы математической теории эмоциональных роботов: монография / Перм. гос. ун-т. Пермь, 2010. 256 с;
-
3. Попов Н.В. Исследование математической модели эмоционального воспитания робота // Современные наукоемкие технологии. 2015. № 12–3. С. 439–443;
-
4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. 8-е изд. М.: ФИЗМАТЛИТ, 2001. Т.1. 680 с;
-
5. Черников К.В. Математические модели роботов с неабсолютной памятью: дис. … канд. физ.-мат. наук. Пермь, 2013.
Research of mathematical model of conflicts in a group of robots
Список литературы Исследование математической модели конфликтов в группе роботов
- Андерсон Дж. Дискретная математика и комбинаторика. М.: Вильямс, 2004. 960 с;
- Пенский О.Г., Черников К.В. Основы математической теории эмоциональных роботов: монография/Перм. гос. ун-т. Пермь, 2010. 256 с;
- Попов Н.В. Исследование математической модели эмоционального воспитания робота//Современные наукоемкие технологии. 2015. № 12-3. С. 439-443;
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. 8-е изд. М.: ФИЗМАТЛИТ, 2001. Т.1. 680 с;
- Черников К.В. Математические модели роботов с неабсолютной памятью: дис. канд. физ.-мат. наук. Пермь, 2013.


