Исследование математической модели воспитания группы роботов
Автор: Ощепкова Н.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (44), 2019 года.
Бесплатный доступ
Сформулированы теоремы, описывающие свойства воспитания группы роботов-цифровых двойников, вводятся коэффициенты групповой памяти роботов и исследуются свойства этих коэффициентов. Показано, что при большом количестве тактов непрерывного воспитания равномерно забывчивых роботов с равноценными эмоциями группа также будет обладать свойствами равномерной забывчивости.
Робот, цифровой двойник, память, воспитание, группы роботов
Короткий адрес: https://sciup.org/147245424
IDR: 147245424 | УДК: 004.8:519.86/.87 | DOI: 10.17072/1993-0550-2019-1-39-43
Текст научной статьи Исследование математической модели воспитания группы роботов
В настоящее время активно разрабатывается теория эмоциональных роботов [1], связанная с созданием цифровых двойников человека и основанная на моделировании эмоций человека [2]. Однако, на наш взгляд, исследованию психологического поведения групп роботов уделено недостаточно внимания.
Одним из немногочисленных примеров, посвященных решению этой задачи, являются работы [3–7]. В этих работах впервые введены понятия группового воспитания роботов и групповой памяти цифровых двойников.
Пусть n – количество роботов в группе, j – порядковый номер робота в этой группе, j = 1, n, Oj ; - коэффициент памяти робота к моменту воздействия на него сюжетом с порядковым номером i, Ojt е(0,1 — 5, ^, 0 < 5 ■ < 1, 5- = const, r i - элементарное воспитание робота j , R – суммарное воспитание робота, полученное им в результате воздействия на него общего количества сюжетов.
В работах [3, 4] показано, что воспитание группы удовлетворяет соотношению
Ri = ri+ OiRi- ,(1)
nn
Z Rj,iZ i=1
где Ri = ------, ri = , nn
n
-
— Z^A .»
-
ei = j^-------.(2)
Z 4 — 1 j = 1
Очевидно, что коэффициент групповой памяти роботов при r i > 0 удовлетворяет соотношению
O i g ( 0,1 — 5 ], 0 < 5 < 1, 5 = const .
Теоремы о групповом воспитании роботов
Cформулируем несколько теорем.
Теорема 1
Если r i > 0, i = 1, ^ ,
Oi g (0,1 — 5],0 < 5 < 1,5 = const, то последовательность R i сходится.
Доказательство
Нетрудно видеть, что равенство (1), описывающее групповое воспитание роботов, полностью эквивалентно соотношению для воспитания индивидуальных роботов, приведенному в монографии [5]. Поэтому доказательство теоремы 1 полностью совпадает с доказательством теоремы 2.5 , приведенной в работе [5].
Теорема 2
Если lim0i = 0 < 1, ri > 0, i = 1,ж, i >ж
lim 0 i = lim
i >ж
i >ж
n
n
Z0 j q j
j = 1
n
Z q
j = 1
Z 0 j q i lim 0 i
j = 1
i >ж
n
Z qj lim 0 i
J i>ж
j = 1
-
0 j
-
i - 1
0 j
1 - 0 j
i - 1
1 - 0 j
-
0 j
i - 1
—
0 j
1 - 0
i - 1
1 - 0 j
то существует предел r i при i > ж .
Доказательство
В силу теоремы 1 справедливо равенство limRi = z < ж.
i >ж
Переходя к пределу при i > ж с учетом условия теоремы 2 о том, что
n
Z j
= 1
n
j 1 - 0
Z q j
= 1
1 - 0 j
= 0 < 1.
lim 0 i = 0 < 1, получим цепочку равенств i >ж
z = lim R i = lim r i + lim 0 lim R i - 1 = lim r i + 0 z , i >ж i >ж i >ж i >ж i >ж
которая влечет соотношение
lim r i =1 1 - 0 I z <ж .
i >ж
Таким образом, мы показали, что для равномерно забывчивых роботов с равноценными эмоциями коэффициент групповой памяти имеет предел.
Поставим следующую задачу:
- определить среднее значение коэффициента памяти 0т группы роботов за m актов.
Очевидно, что для решения этой задачи необходимо найти величину 0т , являющуюся
решением задачи:
Таким образом, теорема 2 доказана .
найти
m min Z| 0m
0 m i = 1 \
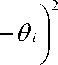
Свойства памяти группы роботов
Легко показать, что 0m удовлетворяет
Пусть верны соотношения 0.= 0 j , j i = q j > 0.
Согласно работе [3] для группы, состоящей из равномерно забывчивых роботов с равноценными эмоциями [4], справедлива формула
соотношению
m
m
Z0i i=1
m
n
—
0 i = j = 1
-
Z O q jj
1 - 0 j
i - 1
1 - 0 j
n
z qj j=1
1 - 0 j
i - 1 .
1 - j]
С учетом соотношения (3) очевидна цепочка равенств
которое с учетом формулы (3) можно записать в развернутом виде:
m
Z i=1
n
Z0^
j = 1
1 - (0^
n
Zqj j=1
1 - 0^
--j
m
В силу положительности элементарных воспитаний равномерно забывчивых роботов группы очевидна цепочка соотношений:
« 1 — 0 i — 1
Ё 0, q
_ У j j 1 — 0,
0i=—------ГГ n l-0i —1
q 0
E j 1 — 0
n
1 — 0, i—1 0.q j j 1—0
1
—
oi i
—
1
qj^^
J
=
E
J*
=
1
вид Подставляя формулу (5) в равенство (4), получим: n m E0 m Найдем предел: n
=
E
0-
J
=
1
Отметим, что следующей задачи: м
=
lim 0„
.
m m ^м найти
min
E
l ©
м
— _2
J
. Легко видеть, что решение задачи (7) удовлетворяет соотношению м m_ lim E 0i m ^м ^^ __________i =1 lim m m ^м В силу справедливости неравенства (6) верна формула n
=
1
Рассмотрим ряд м м
E
0
i
=
E
i
=
1
i
=
1
n
E
°
q
j j
=
1
1
—
o
i
—
1
Пусть
q
=
q
=
const
,
j
=
1,
м
.
В этом случае соотношение (4) примет m m E i=1
n
1 -
0 i
—
1
E 0—
E
J
1
—
J
j
f
1—
0
i
—
1
E
1
—
0
j
m .
Модели равномерной забывчивости группы роботов
Для того чтобы описать качественное поведение среднего коэффициента памяти
©m
, соответствующего формуле (10), построим график при следующих параметрах:
n
=
2,
0
=
0.5,
0
=
0.33,
m
=
1,50
.
Для выполнения численного эксперимента была разработана компьютерная программа, результаты работы которой приведены на рисунке. Изменение среднего значения коэффициента памяти группы роботов n E qj j =1
1
—
oi
—
1
^J
Очевидно, что общий член ряда (9) удо- влетворяет соотношениям: n ]-0*—1 q. 1°-q,
_ _
E
j j
1
—
o
j
E
j j
1
—
0
,
0м = lim Ji = lim----------гУ =— ^ i^м i^м n 1 J i1
E
q
T
j
E
q^,
Полученное соотношение показывает, что с течением времени группа роботов становится равномерно забывчивой, кроме того, ряд (9)
расходится, а так как все члены
Qi
ряда положительны, то справедливо равенство
м
E^-
м
.
i
=
1
Рисунок наглядно демонстрирует, что с увеличением количества тактов средний коэффициент памяти робота приближается к константе. Поэтому при большом количестве тактов в качестве коэффициента групповой памяти робота можно принимать эту константу, а, значит, считать группу роботов равномерно забывчивой. В этом случае при большом значении
m
справедлива формула ©m « © =
const
, а, значит, можно считать, начиная с некоторого большого номера такта
I
, верным соотношение
R
i
-
r
+©
R
—
,
где
i
=
I
,
м
.
Согласно соотношению (11) воспитание
R
i
группы равномерно забывчивых роботов с равноценными эмоциями будет описываться
где n f„,., .Е qi 0 k i =1
1
-0
m
1
-0
•
, _ J-0i приближенно равенством Ri = r-—— где n r = ^ qj , а предельное воспитание группы j=1
R
х
можно приближенно найти по формуле
R
®
r
1
-0
n
J
=
1
1
-
F
m
N
-
1,
kN
-
1
n
0
k
N
-
1
Е
q
i
I
i
=
1
1
- 0
m
N
-
1
1
-0
Л + 0 mN-1 Fm mN-2, kN -2 7
F n
=
0.
m
0 ,
n
0
Аналогично работе [7] параметр "соскучился" можно написать в следующем виде:
(
0
m
N
A
n
“0
*
'
(
1
-0)1
Е
q
i
y^-
к
+ 0 mNFm mN-2, kN-2 .
где
m
>
I
.
При этом
R
i
1
-©
i
s
r-----
1
-0
n j=1 m Е i=1 n
Е
q
fi>
J
=
1
1
-
0
i
-
1
В итоге величина интереса
Д
N
группы роботов к медиа-проекту определится формулой
n Е qj j =1
I
m
Е
i
=
1
1
-
1
-
1 - <
%
i
-
1
1
^
m n Е qj° j =1
1^01
1
1
-
0
А
~ &-
N
а
n
0
kN
(
1
-0
) Z
q
I
1-0
m
N
I
■0
mN
F
I
1
-0
m
N
-
2
J
. (14)
n
Е
q
i
0
m
N
+0
m
N
(
0
1
)
^
-
1
k
с N
-
1
Отметим, что все свойства интереса группы к медиа-проекту при выполнении условия
mx
>
I
будут
аналогичны свойствам
m Е i=1 n
=
1
1
-
0
i
-
1
1
-
0
m n Е qj°j j =1
1
-
0
-
1
1
-
0
интереса к медиа-проекту отдельного равномерно забывчивого робота с равноценными эмоциями (подробно работе,
при этом
0.0Ш
эти свойства описаны в
m
1
Е i=1 n Е0
j
=
1
1
-
0 i
-
1
^j
1
-
0
i
-
10
m
1
n j =1
1
-
0
m
Таким образом, на основе численного эксперимента показано, что для равномерно забывчивых роботов в группе с равноценными эмоциями каждого робота при большом количестве тактов можно считать группу роботов равномерно забывчивой и поэтому, если группа роботов воспитывается с помощью медиапроектов, аналогично работе [7] параметр "надоело"
а
для полного воспитательного цикла с порядковым номером
N
примет вид
n а “Е q0 mN +0"' ч(в- 1)F..-„.._ • аэ i=1
Формулы, аналогичные соотношениям (12)-(14), можно получить при замене величины
0
на значение
0
х
, что также будет определять приближенную равномерную забывчивость группы роботов при большом значении тактов
m
непрерывного воспитания.
Заключение
Таким образом, в настоящей статье показано, что при большом первоначальном количестве тактов непрерывного воспитания группы равномерно забывчивых роботов с равноценными эмоциями группу роботов можно считать равномерно забывчивой, и все свойства этой группы аналогичны свойствам отдельного робота.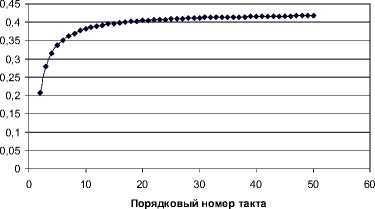
Список литературы Исследование математической модели воспитания группы роботов
- Пенский О.Г., Черников К.В. Основы математической теории эмоциональных роботов: моногр. Пермь: Перм. гос. ун-т. 2010. Текст парал. рус., англ. 270 с.
- Пенский О.Г., Кузнецов А.Г., Ощепкова Н.В. Математическая модель и алгоритм накопления информации роботом с неабсолютной памятью // Вестник ЮУрГУ. Сер. Компьютерные технологии, управление, радиоэлектроника. 2018. Т. 18, № 2. С. 142-148.
- Пенский О.Г., Черников К.В. Математические модели психологических установок роботов // Искусственный интеллект и принятие решений. РАН. М., 2013, № 2. С. 28-32.
- Пенский О.Г., Черников К.В. Основы математической теории эмоциональных роботов: моногр. Пермь: Перм. гос. ун-т. 2010. Текст парал. рус., англ. 270 с.
- Pensky O.G., Sharapov Y.A., Chernikov K.V. Mathematical Models of Emotional Robots with a Non-Absolute Memory // Intelligent Control and Automation. USA. 2013. Vol. 4. № 2. P. 37-42.
- Pensky O.G., Mihailov V.O., Chernikov K.V. Mathematical Models of Receptivity of a Robot and a Human to Education // Intelligent Control and Automations. USA. 2014. Vol. 5, № 3. P. 25-29.
- Пенский О.Г., Шарапов Ю.А., Ощепкова Н.В. Математические модели роботов с неабсолютной памятью и приложения моделей: моногр. Пермь: Изд-во ПермГУ. 2018. 310 с.


