Исследование микрорельефа поверхности сильвина с помощью метода Хёрста

Механические свойства минеральных агрегатов существенным образом зависят от их микроструктуры: размеров, геометрии и свойств зерен, размеров и механических параметров межзеренных границ [1, 2]. При изучении микромеханических характеристик зерен соляных пород, таких как модуль упругости и твердость, на современном экспериментальном оборудовании [3] необходимо принимать во внимание "качество" исследуемой поверхности – наличие на ней случайно расположенных микропор, микротрещин и иных дефектов. Кроме того, сведения о микрогеометрии поверхности кристаллов могут быть использованы при выяснении механизмов разрушения и построении соответствующих математических моделей.

В предлагаемой статье делается попытка оценки вероятностных характеристик микрорельефа поверхности сильвина на основе

• *Работа выполнена при финансовой поддержке аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (проект 2.1.2/5135)

2.    Экспериментальные измерения

измерений профиля поверхности на приборе NanoTest-600 путем определения параметров Херста отдельных сегментов экспериментального ряда данных.

Кристаллы сильвина (KCl) имеют кубическую структуру и входят наряду с галитом (NaCl) в состав биминеральной породы сильвинита – основного сырья для получения калийных удобрений.

Микрорельеф поверхности зерна сильвина измерялся на приборе NanoTest-600 вдоль системы 20 параллельных линий длиной 870 мкм и расстоянием между ними 10 мкм в точках, расположенных на приблизительно равных расстояниях друг от друга (0,34 мкм). Количество измерений на каждой линии составляло, таким образом, около 2500 точек. Величина усилия на конический индентор при сканировании профиля 1 мН, погрешность измерений высоты (профиля) не превышала 1 нм.

Вид исследуемой поверхности сильвина приведен на рис. 1, отражающем микронеоднородности различной геометрии, размеров и ориентации.

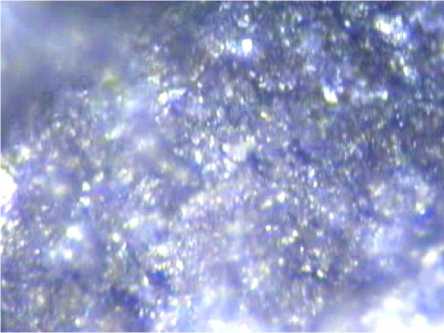
Рис. 1. Вид поверхности сильвина при увеличении 1100 х (размер отрезка 20 мкм)

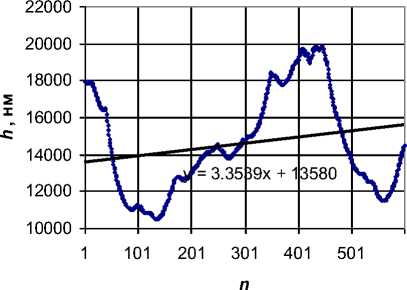
Рис. 2. Рельеф поверхности и линия регрессии

Типичный вид профилограммы приведен на рис. 2. Максимальный размах изменения профиля по высоте составляет на этом участке 9,5 мкм, прямая линия – линия регрессии, показывающая среднее изменение рельефа. В дальнейшем при обработке данных значения высот во всех случаях модифицировались таким образом, чтобы линия регрессии (рис. 2) была горизонтальной.

3.    Показатель Херста

Показатель (параметр) Херста H [4] определяется как угловой коэффициент наклона линии регрессии эмпирической зависимости (1), построенной в двойных логарифмических координатах

R / S = ( т /2) H ,             (1)

где R / S - нормированный размах, т - период (длина ряда) наблюдений.

Нормированный размах определяется через разность

R ( т) = max X ( t , т) - min X ( t , т ) 1 < t <т                     1 < t <т

накопленного максимального и минимального отклонения случайной величины x ( t ) от ее среднего значения xx ( т )} за время т :

X ( t , т ) = i [ x ( и ) - (х ( т ) )] ⁽³⁾ и = 1

и стандартное отклонение

S^(т ) = у fi k o- x r ))!, т t = 1

1 т

(x ( т )) = -£ x ( t ) . ⁽⁴⁾ т t = 1

Метод нормированного размаха применяется обычно при обработке временных рядов, но есть примеры его использования в случае, когда роль времени играет пространственная координата, например в работах [4, 5].

Теоретически доказано, что для случайного процесса (броуновского движения) показатель Херста H = 0,5. Псевдослучайный сигнал (стандартный генератор случайных чисел) дает H = 0,56.

На большом эмпирическом материале было показано [4], что для многих природных процессов и явлений показатель Херста лежит в диапазоне H = 0,72 – 0,74 – это справедливо для процессов, имеющих трендовую составляющую (наличие памяти и сохранение имеющейся тенденции). Для детерминированного сигнала получен показатель H =1,026.

Антиперсистентные системы, проявляющие цикличность (после роста идет спад), дают значения показателя H < 0,5.

Интерес к показателю Херста при исследовании геометрии фрактальной кривой обусловлен также тем, что он связан с фрактальной размерностью D соотношением

D = 2 - H . (5)

4.    Статистическая обработка данных

Множество точек (около 2500), расположенных вдоль линии, в которых замерялась высота профиля, разбивалось на три примерно равные группы точками с порядковыми номерами 800 и 1600. От каждой из них в обе стороны были отложены интервалы по 300 точек, концевые точки которых имеют порядковые номера 501, 1100 и 1301, 1900 соответственно.

Для каждого интервала рассматривалось три варианта статистической обработки:

в  прямом  направлении  (501→1100,

1301→1900);

в обратном направлении (1100→501,

1901→1300);

в обоих направлениях от центра (800±300, 1600±300).

Для первых двух вариантов использовался метод, предложенный самим Херстом [4], для третьего варианта использовался модифицированный метод. Физический смысл третьего варианта состоит в определении статистической закономерности микрогеометрических характеристик при удалении от некоторого "центра" в обе стороны вдоль выбранной прямой.

На рис. 3 показана зависимость (1), построенная в логарифмических координатах, и соответствующая линия регрессии, по которой определялся параметр Херста.

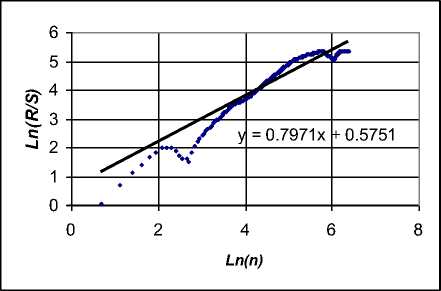
Рис. 3. Зависимость параметров распределения и линия регрессии для второй группы точек (обратное направление)

Результаты обработки свидетельствуют о наличии статистической закономерности трендового характера с показателем Херста, несколько превышающим диапазон 0,72 – 0,74.

На рис. 4 для этого же диапазона представлена зависимость текущего параметра Херста от количества экспериментальных точек (длины ряда). Налицо переход от детерминированного поведения к постепенному случайному трендовому характеру, стабилизации значения H . Подобная нетривиальная зависимость показателя от длины ряда обсуждается в работе [5], где выдвинуто предположение, что для очень большого числа наблю- дений при n → ∞ ожидается стремление процесса к броуновскому движению, когда эффекты памяти стремятся к нулю: H → 0,5 .

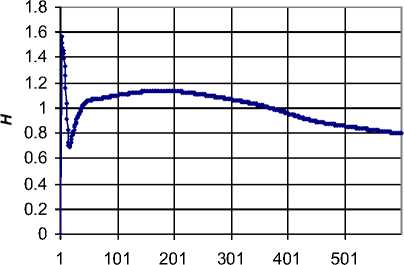
n

Рис. 4. Зависимость показателя Херста от количества экспериментальных точек для второй группы точек (обратное направление )

Результаты вычислений показателя Херста H по двум группам точек в прямом и обратном направлении, а также в обоих направлениях от "центра" представлены в таблице.

Группы точек	Направление
	прямое	обратное	от центра
[501,1100]	0,999	1,114	0,867
[1301,1900]	0,876	0,797	0,566

5.    Анализ результатов

Определение статистических параметров микрорельефа поверхности имеет существенную особенность по сравнению с их определением для временных рядов. Показатель Хёрста, вычисленный по известной схеме (как и для временных рядов), в той или иной степени зависит от выбранного направления в плоскости.

Сравнение результатов для выбранных групп точек с результатами исследования по всему интервалу точек показывает, что ряд в 600 значений может быть недостаточно велик для того, чтобы получить устойчивые значения показателя Херста.

Выбранные группы точек имеют различные значения показателя Хёрста: для первого интервала большие, для второго интервала – меньшие. В соответствии с теорией это означает следующее:

• А)    На втором участке рельеф поверхности ближе к случайному гауссовскому рас-

• пределению (H = 0,5), но с наличием определенного тренда; на первом участке рельеф поверхности обладает почти детерминированным распределением.

Б) Поверхность первого участка менее изрезана, фрактальный показатель D = 2 - H = 0,9-1,0, по сравнению с поверхностью второго участка, где D = 1,1 – 1,2.

• В)    Значения показателя H , близкие к единице и даже большие единицы, возможно, говорят о недостаточности количества экспериментальных данных. Это косвенно подтверждает факт, что при вычислении показателя Херста на интервале данных, использующем все экспериментальные точки, таких высоких значений показателя не наблюдалось ( H < 1).

Устойчивое отличие показателей Херста на разных отрезках, полученное как в прямом, так и в обратном направлениях, говорит о качественно различном характере геометрии поверхности отдельных сегментов кристалла сильвина.

В заключение авторы выражают искреннюю благодарность профессору С.А.Кон стантиновой за обсуждение постановки задачи и результатов исследований.