Исследование одной граничной задачи для интегро-дифференциального уравнения с главной частью Коши - Римана

Как известно, различные прямые и обратные задачи для уравнений Коши — Римана и Лапласа были рассмотрены в работах [1–9]. Здесь будем рассматривать задачу Стеклова для интегро-дифференциального уравнения первого порядка с общими линейными граничными условиями.

Исходя из фундаментального решения уравнения с главной частью Коши — Римана строятся основные соотношения. Из этого основного соотношения отделяются необходимые условия, которые содержат сингулярности. Регуляризируя эти сингулярности своеобразным методом, получаем регулярные соотношения, которые совместно с заданными граничными условиями позволяют свести поставленную задачу к интегральному уравнению Фредгольма второго рода.

1 Постановка задачи

В ограниченной области D с R ² рассмотрим задачу:

u(x) + i u(x) + a(x)u(x) + [k(x,n)u(ndn = 0, x e D,

∂x∂

b l

u(x 1, Y2(xi)) + a(xi)u(xi, Y1(x 1)) = A I" [A(x 1,П1)u(П1, Y1 (П1)) + a 1

+ в2(x1, П1)u(П1, Y2 (П1))]dn1, x 1 e [«1, b ], где D — ограниченная и выпуклая по направлению x2 область, Ле C — параметр.

Если область D спроектировать на ось x параллельно оси x2 , то гра ница Г=dD разбивается на части Г1 и Г2, уравнения которых при x1e[a1,bj имеют вид: x2 =/1(x1) и x2 =/2(x1).

Известно, что фундаментальное решение уравнения Коши — Римана имеет вид [10]:

U ( x - 0 =— 2 п x ₂

.

- ^2 + i(x1 - 51)

[ u ( x)U ( x - £ ) cos(v, x ₂ ) dx - [ u ( x ) ^⁽ x —^ ) ∂ x

Γ

- i j u ( x )

D

D          x 2 x.

d.x + i I u ( x)U ( x - ^ ) cos(v, x_x )dx -

Γ

^^^{( x} —^ ) dx + J a ( x ) u ( x)U ( x - ^ )dx + j u ( n ) d n j U ( x - ^ ) K ( x , n )dx = 0,

-1

D

DD

или j u(x)U(х - d)[cos V, х 2)+icos V, х1)] dx+j u(n) dr][a(rj)U(n - d) +j U(x - d)K(x, n) dx =

г

D

= j и(х)

D

d U ( x - d ) + i d U ( x -d ) d x ₂          3 x 1

D

[<), -■ D,

dx = [ u ( x ) 5 ( x -d ) dx =< 1

^J              | 2 u( d ), - L

D

где v — внешняя нормаль к границе Г области D .

Как видно из (5), это основное соотношение состоит из двух частей: первая часть является произвольным решением уравнения (1), а вторая часть — необходимым условием. Таким образом, имеет место следующее утверждение.

Теорема 1. Пусть задана ограниченная, выпуклая по направлению х 2 плоская область D , где граница Г является линией Ляпунова,

a(х ), K ( х , n ), a ( x 1 ), Д ( x 1 , n 1 ), в ₂( x 1 , П 1) — известные непрерывные функции своих аргументов и Ле C — параметр, тогда каждое решение уравнения (1) удовлетворяет основному соотношению (5).

• 3    Определение необходимого условия

Основное соотношение (5) представим в следующем виде:

• 1               1 Г       ^м ( X , Y ( X ))      г /                     dx

  - u U , Y i U )) =— I ——---——--- —^{[- cos(} x i , ^T ) + 1 sin x , T ^{) ]}------- +

• ^{2              2} П Y i ⁽ x i )-П Й ) ⁺ i ⁽ x i - ^:)                        ^{cos( x} i ^{, T} ) ⁽⁶⁾

^a 1

+ ...

¹ U ⁽ d 1^, Y 2 ^{( d} i ⁾⁾ =            ^{u (} x¹, ^{Y (}x )) — -^{[ cos(} x i^{, T} ) ^- i sm^ T ^{) ]} — d^- ⁺ ... ⁽⁷⁾

• ^{2               2 n}=Y 2 ⁽ x i ) ^- Y 2^{( d} i ) ⁺ i ⁽ x i ^{- d} i )                         ^cos( x i ^{, T} )

aj где t — касательное направление на границе Г в направлении по воз растанию аргумента xj, (^) обозначена сумма несингулярных слагаемых.

Используя формулы конечного приращения Лагранжа, необходимые условия (6) и (7) представим в виде:

1 1

u (di, Yi(di)) = - -J п ai

^{u (} x i , Y i ^{( x} iY)

^{( x} i ^{- d} i ^{) [ (} Y i' ⁽ ^ i ⁽ x i , d i )) ■ i ]

^{[ 1 -} i Y’ ^{( x} i ^{) ] dx} i ⁺ ...

^{u ( d} i , Y 2 ( 5 1 ))

X ^{6 1          u ( x} 1 , Y 2^{( x} 1 ))

^{п J ( x} 1 ^{- d} 1^{) [ (} Y 2 ⁽ ^ 2^{( x} 1 , ^d 1^{)) +} i ^]

^a 1

■ [ 1 - i Y 2 ( x 1 ) ] dx 1 + ...

4 Выделение сингулярности

В каждом выражении из необходимых условий (8) и (9) содержаться сингулярные слагаемые. Для выделения сингулярности в этих выражениях производим следующие вычислительные преобразования:

^{1 -} i Y k ⁽ x P = ^{1 -} i Y k ⁽ x P + i - i =- + ^{1 -} i Y k ⁽ x P + i Y k ( ^ k ) ^{- 1} =

Y k ⁽ ^ k ) + i Y k ⁽ O k ) + i                  Y k ⁽ ^ k ) + i                  (10)

. . ' '- ) ■ x , k = у

Yk (^k)+i т. к. ok(x1,§1) находится между Х и §1 , то, учитывая (10) в (8) и (9), на-

ходим:

— 1 u ( Х 1, Y 1 ( Х 1 )), , u ( § 1 , Y 1 ( § 1 )) =                е     dx 1 + ...                          (11) π x - ξ a !           1^1 u ( § . Y 2( 5 )) = - 4} u(^ dx + ...                  (12) π x - ξ a.       1 71

5 Регуляризация

Учитывая граничное условие (2), исходя из необходимых условий (11) и (12), создадим следующую линейную комбинацию:

u ⁽ § 1 , Y 2 ⁽ § 1 ^{)) - a (} § 1 )u ( § 1 , Y 1 ⁽ § 1 )) = ^- — Г u ⁽ x ¹, ^{Y 2}( ^{Х 1))} dx 1 - ^п-     ^x 1 - § 1

- — j [( a ( § 1 ) - a ( Х 1 )) + a ( Х 1 )] u ⁽ x ¹’ ^{Y 1 (Х 1))} dx 1 + ... = ⁿ i                             ^x 1 ^- § 1

= - ^it u (П1, Y1 (П1)) dn j в(Х1,П1) π              x -ξ a1                                a 1      1      11

Xi b                 b dx - П J u (П1, Y2(П1))dn1 • j

a

a

^{в{ x} ' - ^{n1 )} dx 1 + ..

^x 1 ^- § 1

Таким образом, утверждаем следующую теорему.

Теорема 2. При условиях теоремы 1 и если a(x1) принадлежит некото рому классу Гельдера, тогда выражение (13) является регулярным.

X b

" ^{( 4} 1 . / 2 ^{( 4} 1 )) = — J [ A ^{( 4} 1 . П 1 ) " ⁽ П 1 . / 1 ⁽ П 1 )) + ^в 2 ^{( 4} 1 . П 1 ) " ⁽ П 1 . / 2 ⁽ П 1 ^{)) ] d} n 1 ^— 2 п

a

и

b                          b

^— — j u ⁽ n 1 . / 1 ⁽ n 1 )) d n 1 •/

2 n ^{J                   J}

a 1

a l

P i ^{( x} 1 . П i )) ^x 1 ^{— 4}

Xi bb dxi — 2n J"(n 1 ’/2(n 1))dn 11

a l

a 1

№vnl dx 1

^x 1 ^{— 4}

—

—-1 " ( x . / 1 ( x X⁴—a x) dx +- J "^! X ' '-x *^{1 4—}^ ^{x )} dx +

2n‘           x — 4      I4 ^ir,)+1x aa

+ a ⁴ - ux . ^{Y (} x ). ^ / xdx —4 " ( x . к ⁽ x» [ 1 — / ( x ) ] dx —

^{2 n J} /Уд ) ⁺ i    x ^{— 4        2 n} J / 1 ⁽ x ) ^— y ₂ ^{( 4} ) ⁺ i ⁽ x ^{— 4} )

aa

—

ag) ',--- Чщй»--- [ 1 — x )d ₊

2 t J / , ( x ) — / 1 ( 4 ) + i ( x — 4 ) a

+ ₂ L J "( n d

1            r      K(x. n )dx

4 1 ^— / 2 ^{( 4} ) ^{+ i (} n ^{— 4} ) ^{+ J} x 2 ^— / 2 ^{( 4} ) ⁺ i ⁽ x ^{— 4} )

—

— a ⁴ " nn -----¹----- +( ^{K ( x n )dx}

2 л D      \_П1 ^— / 1 ^{( 4 ) +} i ⁽ n i ^{— 4} 1 ) D x 2 ^— / 1 ^{( 4 ) +} i ⁽ x 1 ^{— 4} \

⁴ 1 ^g[ a l. b 1^],

X b

" ^{( 4} 1 . / 1 ^{( 4} 1 ⁾⁾=—-— C^{[ e ( 4} 1 . П 1 ) " ⁽ n 1 . / 1⁽ п 1 ^{))+ [ e} 2 ^{( 4} 1 . п 1 ) " ⁽ П 11 . / 2⁽ n 1 ^{)) ] d}n 1 ⁺ 2 ^{na ( 4} 1 ⁾ a

Xi

+ 2na(4)

h . / ( n )dn • f ^в ■ ⁽ x ■ . ⁿ ■ ⁾⁾ dx +——— f u ( n . / ( n )dn f ^в 2 ⁽ x 1 . ^{П 1))} dx +

■’^?lV■^№■ J x 1 — 4 1        2 na ( 4 )J ^U1’^/2U1^^flJ x 1 — 4 1

⁺        J " ⁽ x L ^/ 1 ^{( x} 1^{)) O4} - 0 ⁽ x 1 ) ^dx 1

Y^ax⁴) a               ^x 1 ⁴ 1

—

i     b f ^U ( ^X i , ^Y 2 ( ^X i )) / 2 ^{( д} 2 ^{) —} / 2 ⁽ x 1 ) dx

^ Ta^⁴ ) ^J / ^ ( З ) ) ⁺ i     x 1 ^{— 4} 1

—

—

J_ b r " ⁽ x 1 . / 1 ⁽ x j )) / ‘^{( д} 1 ^{) —} / J⁽ x 1 ) dx +

2n J /‘(З) + i     x1 — 41

a1

1        b 1

2 ^ 0( 4 )^J / 1 ⁽ x 1 )^— / 2^{( 4} 1 ) ⁺ i ⁽ x 1 ^— 4 1 ) ^a1

" ^{( x} 1 . / 1 ^{( x} 1 ))

■ [1— /(x 1 ) ] dx 1 +

1 b 1

+

^{2 n}a₁/ 2 ^{( x} 1 )^— / 1 ^{( 4} 1 )⁺ i ^{( x} 1 ^{— 4} 1 )

" ⁽ x 1 . / 2 ⁽ x 1 ))

^[ 1— i/ 2 ( x 1 ) ] dx 1 —

1 2 na ( 4 )

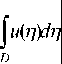
n 2 ^— / 2 ^{( 4} 1 ) ⁺ i ^(?7 1 ^{— 4} 1 )

г      K ( x . n ) dx

^J D x 2 ^— / 2 ^{( 4} 1 ) ⁺ i ^{( x} 1 ^{— 4}\

+

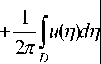
n 2 ^— У 1^{( 4 ) +} i ⁽ n 1 ^{— 4} 1 )

г      K ( x . n ) dx

^J D x 2 ^— / 1 ^{4 +} i ^{( x} 1 ^{— 4} 1 )

. ⁴ 1 ^{e[ a} 1 . b j

Объединяя полученные уравнения (15) основного соотношения (5), будем иметь:

и (16) с первым выражением из

u ® =- —^{u ( x} „ М x ,» [ 1 - _wx )_k + О u ⁽ s , ^{Y 2} x ,» 2 n J Y (t) - 5 , + i ( x ’ - { У '"'^ 2 n J у , (^) - g + i ( * . - 6 )

•^{[ 1 -} i Y 2 ^{( x} ) ] dx + J _ J u n d

П 2 ^{- g} 2 ⁺ i П ^{- g} 1 )

+ г     K ( x, n ) dx

D ^x 2 ^- g . ⁺ i ^{( x} 1 ^- g )

, g e D.

Таким образом, устанавливаем следующее утверждение.

Теорема 3. При условиях теоремы 2, если имеет место условие (14), тогда в задаче (1)-(2) имеет место фредгольмовость.

Мы показали, что при условиях теоремы 3 граничная задача (1)-(2) сводится к системе интегральных уравнений Фредгольма второго рода с регулярным ядром.

Замечание 1. Решая систему (15), (16), для любого Ae C определяем u ( g , y ₂( 5 1 )) и u g , Y i ( 6 i )) через интеграл по области D , который содержит u ( n ).

Подставляя найденные и ( g , у 2 ( 6 1 )) и u g , Y ₁( 6 ₁)) в уравнение (17) относительно и ( g ) при ge D , получаем однородное интегральное уравнение Фредгольма второго рода с регулярным ядром, зависящее от параметра Ae C .

Замечание 2. Собственные значения и собственные функции определяются из полученного интегрального уравнения относительно и(g), geD.

Заключение

Как известно, для многомерного дифференциального уравнения в отличие от обыкновенного дифференциального уравнения число граничных условий совпадает с половиной порядка рассматриваемого уравнения. Поэтому как в курсах уравнений математической физики, так и в курсах уравнений с частными производными граничные задачи рассматриваются в основном для уравнений четного порядка, для уравнения Лапласа с одним из граничных условий Дирихле или Неймана или же Пуанкаре, для бигармонического уравнения (4-го порядка с двумя граничными условиями). Уравнение Коши — Римана является уравнением эллиптического типа первого порядка. Н. Бегер для уравнения Коши — Римана рассматривает задачу Дирихле. Это некорректная задача. Поэтому он предполагает, что данные задачи Дирихле удовлетворяют полученным в работе необходимым условиям. Нами показано, что одно нелокальное граничное условие достаточно для уравнения Коши — Римана. Представленный подход к решению исследуемой задачи может дать обоснованный толчок к получению решений граничных задач, имеющих соответствующую постановку.