Исследование степени однородности цементогрунтовой смеси методом математической статистики

В настоящее время одной из важных задач федеральной целевой программы «Устойчивое развитие сельских территорий на 2014‒2017 годы и на период до 2020 года» является переход дорожного строительства на инновационный путь развития [1]. Переход обеспечивает приоритетное использование новейших эффективных технологий и материалов с целью увеличения надежности и сроков службы дорожных сооружений, снижения стоимости строительства, повышения экологической безопасности. Применение новых технологий и материалов ‒ важнейшая задача в области современного строительства и строительного материаловедения. Один из основных путей снижения стоимости ‒ применение местных материалов, в том числе грунтов, обработанных вяжущим материалом, т. е. цементогрунта.

На современном этапе в России и зарубежных странах накоплен значительный опыт применения технологии укрепления грунтов для строительства конструктивных слоев дорожных одежд автомобильных дорог. Как метод он эффективен в местах, где отсутствуют запасы каменных материалов.

Исследование процессов структурообразования, применение технологии перемешивания ‒ основные возможности формирования цементогрунтовых композитов.

Методы исследования

Экспериментальные исследования, выполненные ранее, показали, что гетерогенная структура зависит от типа грунта, ее можно улучшить рецептурно-технологи-ческими факторами [3] и способами перемешивания [4].

Известно, что рассеивание компонентов при перемешивании ‒ величина случайная и подчиняется закону нормального распределения Гаусса и законам математической статистики. Используя метод статистического анализа, проведена обработка полученных данных с помощью описательной статистики [5]. Одна из задач статистики состоит в том, чтобы проанализировать и обработать данные, полученные в ходе эксперимента. Описательная статистика позволит описать и воспроизвести в виде таблиц и графиков данные, вычислить среднее распределение его размах и дисперсию.

Воспользуемся методом вероятностной выборки, единственным, позволяющим делать правильные выводы по выборке. Воспользуемся выборкой без возврата, когда любой объект не может попасть в выборку более одного раза, т. е. когда все объекты выборки всегда разные [5]. При использовании случайной выборки обеспечивается репрезентативность. Применение таблицы случайных чисел или генератора случайных чисел является одним из способов извлечения случайной выборки для получения номера объекта, который должен быть выбран из генеральной совокупности.

Для обнаружения общих свойств совокупности и выявления закономерности необходимы обобщающие количественные показатели, их называют показателями описательной статистики. Среди них показатель средней величины характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Один из распространенных видов средней величины ‒ средняя арифметическая, ее вычисляют по формуле x Z,                                  (1)

n где n – численность совокупности.

Для определения структуры представленных данных используем особые показатели, к которым относят моду и медиану. Для нахождения медианы воспользуемся формулой

N = ( n + 1)/2,                                         (2)

где n – число единиц в совокупности.

Для определения численного значения медианы ‒ формулой n + 1

S ( - 1)

M e = X + І              .                                       (³)

f M e

Чтобы найти конкретное значение моды, используем формулу

Mo = X» + I m. _    ?       V ,               (4)

⁽ f Mo ^f Mo - 1 ) ^{+ ( f} Mo ^f Mo + 1 )

где Х Мо – нижняя граница модального интервала; I Mo ‒ величина модального интервала; f _Mo - частота модального интервала; f _{Mo - 1} - частота интервала, предшествующего модальному; f _{Mo + 1} - частота интервала, следующего за модальным.

Размах выборки – самый доступный абсолютный показатель

R s = X max — X min .

Для более точной характеристики вариации признака на основе учета его колебаний используются другие показатели [6]. Определяют среднее линейное отклонение как

| x, - x | d = ^^—I.                        (6)

n

Среднее квадратическое отклонение позволяет оценить степень разброса случайных значений относительно средней величины

C T =

n

Z ( x.- x )²

i = 1

n

.

Дисперсия ‒ это средний квадрат отклонений индивидуальных значений признака от его средней величины

2    Z ( x . - x )²

C =--------

.

n

Средняя ошибка характеризует стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности, зависит от дисперсии генеральной совокупности и объема выборки n

M =

Средняя ошибка выборки μ используется для расчета предельной ошибки выборки ∆ х и вычисляется соотношением

∆ _х = t ⋅ µ ,                                          (10)

где t – коэффициент доверия (определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования).

В статистическом исследовании, кроме показателей вариации, выраженных в абсолютных значениях, используют показатели вариации в относительных величинах [6]. Рассчитывают их как отношение размаха вариации к средней величине признака (V R , коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (V a , линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (V σ , коэффициент вариации) и будут выражать в процентах. Относительные показатели вариации вычисляют по формулам

VR = RS ⋅100%;     Va = d ⋅100%;       Vσ =σ⋅100%.(11)

xx

Основной показатель однородности при статистической обработке выборочных срезов как на супеси, так и на суглинке, ‒ коэффициент вариации, равный [5]

Сv =σ,(12)

м где σ ‒ среднеквадратичное отклонение, которое рассчитывалось по программе в МS Excel стандартным отклонением; м ‒ математическое ожидание (среднее значение) [5].

Для оценки однородности смеси рассчитаем коэффициент вариации по формуле

µ = ^S ₂ 100%,                               (13)

σ ²

где S ² ‒ эмпирическая дисперсия выборки; σ ² ‒ полная дисперсия генеральной совокупности.

Рассчитывают эмпирическую дисперсию выборки

z

∑ ( y_i - y )²

S ² = ^{i = 1}             ,                                          (14)

z - 1

где z ‒ число проб; y ‒ среднее значение выборки.

Среднее значение выборки из определенных проб будет иметь вид

1z y = ∑ yi .                                (15)

z i = 1

С помощью математической статистики оценка однородности определяется как среднеквадратичное отклонение концентрации одного из компонентов смеси, это обусловливает ее использование для оценки однородности двухкомпонентных смесей.

Следовательно, основной целью процесса перемешивания является равномерное распределение компонентов по всей генеральной совокупности.

Результаты исследования

Экспериментальные исследования, выполненные ранее, показали, что однородность распределения вяжущего зависит от типа грунта [2; 3]. Основной показатель однородности при статистической обработке выборочных срезов различных грунтов, укрепленных вяжущим ‒ степень их перемешивания. Для оценки однородности перемешивания предлагается использовать случайную выборку, которая представляется репрезентабельной и позволяет перенести выводы статистической обработки выборки на генеральную совокупность [4; 6]. На рис. 1‒2 показаны гистограммы, полученные с помощью надстройки в MS Excel «Анализ данных» → «Гистограмма» [6]. В таблице представлены описательные статистики, выполненные как на супеси, так и на суглинке с помощью программы → «Описательная статистика» [6].

Описательная статистика

Показатель	Суглинок	Супесь
Среднее	40,8	45,85
Стандартная ошибка	1,426442022	1,19489
Медиана	40	46
Мода	40	46
Стандартное отклонение	6,379242654	5,343712
Дисперсия выборки	40,69473684	28,55526
Эксцесс	-0,37770415	-0,33432
Асимметричность	0,117156577	-0,05012
Интервал	24	20
Минимум	29	36
Максимум	53	56
Сумма	917	917
Счет	20	20
Коэффициент вариации	0,153353987	0,116548

Из таблицы видно, что коэффициент вариации на суглинке составляет 15,3 % , на супеси – 11,6 %.

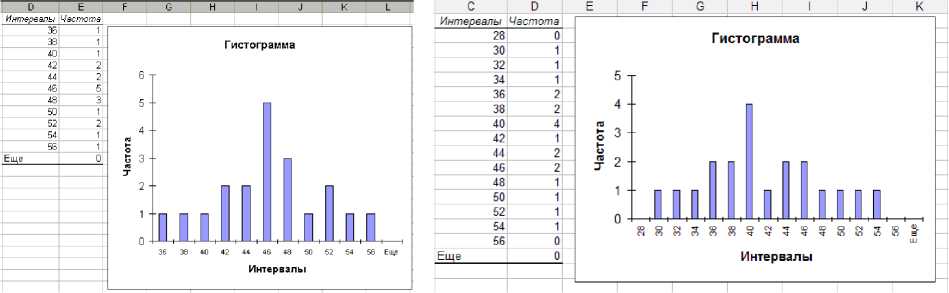
Рис. 1. Гистограмма, построенная для среза, сформированного из супеси

Рис. 2 . Гистограмма, построенная для среза, сформированного на суглинке

Заключение

Анализ полученных результатов показал, что распределение вяжущего в супеси, следовательно, и однородность цементогрунта выше, чем в суглинке. Таким образом, перемешивание супеси с цементом позволяет получить цементогрунт, сравнимый по однородности с цементобетоном, а приготавливаемая таким способом цементогрунтовая смесь обладает высокой степенью однородностью (низкий коэффициент вариации) [4; 6].

M.V. Tarasova, I.A. Trotsenko

Omsk State Agrarian University named after P.A. Stolypin, Omsk

Study of the homogeneity degree of cement-grant mixture with the method of mathematical statistics