Итерационный метод полиномиального дифференцирования для одного класса уравнений сверток

Уравнения сверток играют важную роль при решении многих прикладных задач, которые сводятся к решению дифференциальных, интегральных и интегро-дифференциальных уравнений [1 –4] .

Рассмотрим уравнение

А * U = W,                                     (1)

где А и W — известные функции, U — неизвестная функция. При решении задач идентификации в роли A выступает аппаратная функция, под U подразумевается входной сигнал, под W — выходной сигнал.

Если рассматривать уравнение сверток ( 1 ) в смысле обобщенных функций, то хорошо известен метод решения таких уравнений в пространстве обобщенных функций медленного роста с применением преобразования Фурье.

В общем случае задача ( 1 ) не имеет решения, однако можно выделить классы, в которых уравнение вида ( 1 ) имеет единственное решение [5 –8] .

В данной работе будет рассмотрено уравнение сверток вида ( 1 ), в котором А, U, W — обобщенные функции, принадлежащие пространству D + (R) — пространству обобщенных функций с носителями из [0, то], в котором метод преобразования Фурье не работает. Отметим, что пространство D ’ (R) является сверточной алгеброй [1, 2] .

• 2.    Постановка задачи

Пусть обобщенная функция А е D (R) имеет вид

А = M(t)T (t), где

q

M(t) = УХ’Vp, е C|^q = 0,Vq е N\ {0} , i=0

T (t) е D’. (R) элементарное решение некоторого линейного дифференциального оператора

т

Р (D) = ^a k D ^k , Va k е CK = 1, Vm е N\ {0} ,                    (2)

к =0

здесь ^D = ft .

В сверточной алгебре D + (R) рассмотрим уравнение

А * U = W, VW е d; (R).                              (3)

Известно [9] , если существует элементарное решение уравнения сверток, принадлежащее сверточной алгебре, то оно единственно в этой алгебре. Отсюда следует существование и единственность решения самого уравнения.

Поэтому актуальным становится вопрос отыскания элементарного решения уравнения сверток ( 3 ), принадлежащего сверточной алгебре D^ (R).

• 3.    Итерационные формулы для оператора P(D)

Поскольку оператор Р (D) с постоянными коэффициентами, то его характеристический полином есть т

Р Ю = Е а^^к, ^ е R.

к =0

Множество полиномов, снабженное мультипликативным произведением, является мультиплика-т            п тивным кольцом. Пусть /(ж) = ]V агжг и д(ж) = ^ Ьгжг. По правилу дискретной свертки г=0               г=о т+п f к

/(ж)д(ж) = Е ) Еаг ^ к-г ? ж ^к . к =0    г =0

В частности,

[/ ж = ^Е {^Е : а г а к-гк ^к .

к =0 г =0

Очевидно, [Р(^)] ¹ , VI е N — есть характеристический полином дифференциального оператора [Р (D)] ^{( l )} , здесь I — символическая степень оператора Р (D).

Производная порядка а е N от полного символа Р (£), то есть ^ ^^ — характеристический полином оператора

Р W(D) = a! Е а к Q) (D) ^{к -} “ ,

где а = 0,1,..., т, Р ^т = т!, Р И (D) = Р (D).

Пусть [Р(D)] ^{( l )} есть 1-ая символическая степень опреатора Р (D), I е N\ {0}. Обозначим через Р l“^ (D') оператор, характеристический полином которого есть ^ [Р(£)] ¹ . Тогда

1т

Р l (D) = [Р (D)f ^l = Е Ь к (а к )D ^к ,                            (4)

к =0

где Ь* к (а _к ) выражаются по правилу свертки через коэффициенты а _к оператора Р (D).

При а = 1,2,..., I имеем

Р^ ¹ (D) = Z E f ^a _к 1^Р ^{[ к +1}Ч D)P -- ^{1 - к}Ч D).                      (5)

к =0

• 4.    Действие оператора P _q +i ( D ) на М ( t)T

Применим расширение теоремы Лейбница на случай, когда роль обычного оператора дифференцирования играет l-ая итерация

Pi(D) := [Р(D)](l) дифференциального оператора Р(D). При этом получим

i- i P i ( D ) {М(t)T } = У - М ( a ) (t) P^ (D)(T).                       (6) “ =0 а’

Предположим сначала, что 1 < т < q.

Поскольку Т — элементарное решение оператора Р (D), то

Р (D)(T) = 5,                                          (7) где 5 — мера Дирака. Отметим также, что

Имеем

М ( “ ) (t) = a! р р 3 Д V*,                          (8) j=“    ' 7 М ( q ) (t) = p q q!, Р [ m ] (D) = т!, Р [ “ ] (t) = 0, Va > т, a G N. Р (D) {М(t)T } = V Дм ( “ ) (t)P [ “ ] (D)(T) a! “> 0 = М(t)P(D)(T ) + V Дм ( “ ) (t)P [ “ ] (D)(T) a! “> 1 = М(t)5 + V Lm ( a ) (t)P [ oHd )( T ) a! a =1 = m (t)5 + ^T У^РРэ (Ja V4p [ “ 1 (D)(T)              (9) a =1 ^ j = a              J = М (t)5 + V J V P 3 (3 p-“ l Р M(D)(T ) a =1 [ j = a              J + 52 »s („т.^^^ j=m   x 7

В силу того, что

	q М(t)5 = < V p j t j ^5 = 3 o 5, [ j =0      J
получим	q Р (D) {М(t)T } = P o 5 + тД V p j 3 )t j - m I T т j = m ⎧                 ⎫                                   (10) m- 1 I q      / \       I + v sE P j a t j - “y [“] ( d )( t ). а =1 1 j =“    x 7       1

С учетом ( 5 ), ( 6 ) и ( 8 )

P q +1 (D) {М(t)T } =

= (q +1) ⁵⁵ !е р 3 ( ³ ) f^— “ Ue ( ^a - 1 ) ^pE ^{i — k} ( d ) p ^{[ k +1]} ( d ) | ( t ). 0 =0 [ 3 = 0 W J lk =o ^{k 3}                     J

Используя ( 7 ), получим

P q +1 (D) {M(t)T } =

=(q+1) ⁵⁵1 e Р з ( 3 ) t ^3— ° 11⁵ ( “ — 1 ) p q—— ^{1 — k ]} ( d ) p ^{[ k +1]} ( d ) I (5)

0=0 [3=0             J lk=0 V                                J или

p _q +i(D) { m ®т } = (q +1) ^{55 j} e р з ^) 1 o =0 ^[ 3 = o    ^X )

0 — 1

x E Г _k ) t ^{3— 0} { p q—— ^{1 — k ]} (D)P ^{[ k +1]} (D) } (5). k =0

Вычислим

t ^{3— 0} {p q — ¹

тэ [0— 1 — k] здесь оператор Pq _— i

(D)p ^{[ k +1]} (D) — опреатор порядка не выше чем

{m(q — 1) — [a — 1 — k}^- + {m — (k + 1)} = mq — a.

Следовательно,

mq—o pq——1—k]P[k+1](D)(5)= E аР 1)5(s).

s =0

Отсюда t3—0 ^p,[0—1—k]p[k+1](D)} (5) =

mq—o

E

_Q ( ^{q — 1)} t ^{3 —} ° 5 ^{( s )} ,

s =0

где коэффициенты a s ^{q —} 1) выражаются через коэффициенты оператора p (D) с помощью правила дискретной свертки.

Вычислим t ^3— ° 5 ^{( s )} :

< t ^3—o 5 ^{( s )} ,_v >  = (—1) ^{( s )} <  5, ( t ^{3 —} »^{(S )} >

	= (—1) ( s ) <5, E f S ) ( t 3 — 0 ) ( p ) ^ ( s — p ) > p =0 ^)' (12) = (—1) ( s ) <  5, L _ j (3 — a )Vs— ( 3— 0 )) > = (—1) ( s ) Q — a) (3 — a)!(—1) ( s — ( 3— 0 )) < 5, ^ > .
Следовательно,	t 3—0 5 ( s ) = ( . 8 ^(3 — a)!(—1) ( 3 — 0 ) 5 S — ( 3 — 0 )
и	t 3 — 0 { p q— — 1 — k ] (D)p [ k +1] (D) } (5) = m3z.0       / s \                                               (13) = E a*P— 1)( ■    а)( 3 — a)!(—1) 3 — 0 5 ( s— ( 3—0 )) . 3 = 3 — 0               3

Подставляя ( 6 ) в ( 11 ), получим

P q +1 ( D) {M(^Т } = (q + 1) ^E (-1) “ ^E P ₃ (-1) ³

“ = ⁰       3 = a

X

a — 1 , _1X mq-a        ,      .

E t - 0 E « 8г⁴ С -J (з - «)^ ^{-a-a ))} k =0 e         8 = 3 — a         e '

Аналогичные рассуждения в случае когда т >  q >  1 также приводят к формуле ( 14) . Отметим, что в случае т = 1 используется классический метод предварительного дифференцирования.

Таким образом, без потери общности можно утверждать, что

P q ₊1 (D) {M(t)T } = L(D)(5),

где L(D) — обыкновенный дифференциальный оператор с постоянными коэффициентами порядка не выше чем mq:

L(D) = (q + 1) E (-1) “ ЕТ ^ (-1) ³ “ = ⁰       з = “

(о

X

а— 1          mq - a

E С, О E ^^q—1 k =0           8 = 3 — “

(з-J

(з - a)!D ^{s — ( 3 — а )} .

• 5.    Элементарное решение уравнения сверток

Пусть 8 (t) — элементарное решение уравнения ( 3 ), тогда

M(t)T *8 (t) = 5                                     (17)

в сверточной алгебре Т>'₊ .

Применяя оператор P _q +1 (D) к уравнению ( 17) , с учетом формулы ( 15) , получим в Т> '₊

L(D)8 (t) = P q +1 (D)(5).                                     (18)

Теорема Мальгранжа-Эренпрайса [10] или [11] утверждает существование элементарного (фундаментального) решения любого линейного дифференциального оператора с постоянными коэффициентами, а если оно принадлежит сверточной алгебре, то оно единственно [9] .

Пусть E(t) — элементарное решение оператора L(D), принадлежащее D '₊ , тогда в D '₊ имеем:

8 (t) = P q +1 (D)E (t).                                       (19)

Следовательно, у уравнения сверток ( 3 ) существует и притом единственное решение при любой обобщенной функции W G Т>'₊ . Это решение имеет вид

U = 8* W = P q +1 (D) {E * W } .                         (20)

• 6.    Пример

В качестве примера уравнения, имеющего структуру ( 3 ), рассмотрим уравнение:

( t ² T ) * U = W, VW E T> + .

Здесь

M(t) = t ² ,

Т = YY ер sin wt, w где Y(t) — функция Хевисайда,

P(D)(T ) = { (D - р) ⁽²⁾ + w ² } (Т ), р> 0.

Согласно формулам ( 15 ) и ( 16 )

Рз (D) (t2Т) = L(D)5, где

L(D) = 6D ² - 12pD - 2w ² + 6р ² .

В данном случае элементарным решением оператора L(D) является функция

Е (t) = 3YY(f)e^pt sinh ( ^3wt j 6w              3

е (t) e p ; .

Применяя ( 20 ), получим решение уравнения ( 21 ):

U = P 3 (D) {E(t) * W } .

• 7.    Программная реализация итерационного метода полиномиального дифференцирования с помощью системы компьютерной математики Maple

На практике поиск коэффициентов оператора L(D), как правило, связан с громоздкими вычислениями. Однако, предложенный в данной работе метод решения уравнения сверток ( 3 ) поддается алгоритмизации и может быть автоматизирован с помощью систем компьютерной алгебры.

Продемонстрируем реализацию итерационного метода полиномиального дифференцирования с помощью системы компьютерной математики Maple на примере, рассмотренном выше.

Зададим полином М (t) и дифференциальный оператор Р (D)

M:=t->tA2:

q:=degree(M(t),t):

m:=2:

a[0]:=pA2+omegaA2:  a[1]:=-2*p:  a[2]:=1:# a[3]:=1:

P:=D->sum(a[k]*DAk,k=0..m):

Вычисляем l-ую итерацию P (D) и оператор P _{q +}i (D). Здесь Pq1 означает P _{q +}i (D).

PL:=L->P(D)AL:

Pq1:=expand(Pl(q+1),D):

n:=degree(PL(q+1));

b:=seq(coeff(Pl(q+1),D,i-1),i=1..n+1);

Находим элементарное решение оператора P q ₊₁ (D).

eq:=sum(a[k]/a[m]*diff(T(t),t$k),k=0..m)=0:

init:=seq((D@@k)(T)(0)=piecewise(k<>m-1,0,1),k=0..m-1): solution:=dsolve({eq,init}):

T:=Heaviside(t)*rhs(solution);

Вычисляем результат применения оператора P _{q +1} (D) к М (t)T(t).

R:=b[1]*M(t)*Tau(t): for i from 2 to n+1 do

R:=R+b[i]*diff(M(t)*Tau(t),t$(i-1)):

end do:

Sq1:=R:

for i from n by -1 to 1 do

Sq1:=subs(diff(Tau(t),t$i)=DAi*Tau(t),Sq1): end do:

Pq1MT:=expand(simplify(factor(Sq1)/(P(D)*Tau(t))));

Вычисляем коэффициента оператора L(D).

S:=Pq1MT: nS:=degree(S,D); C[1]:=coeff(S,D,0): for i from 2 to nS+1 do

C[i]:=coeff(S,D,i-1): end do:

R:=subs(t=0,C[1])*Dirac(t):

for i from 2 to nS+1 do

R:=R+C[i]*Dirac(i-1,t): end do: R1:=simplify(R):

R1:=subs(Dirac(t)=delta,R1): for i from 1 to m*(q+1) do R1:=subs(Dirac(i,t)=DAi*delta,R1): end do:

L:=expand(R1/delta);

L := 6D ² - 12pD - 2w 2 + 6p ²

Находим элементарное решение оператора L(D).

N:=degree(L,D):

A:=seq(coeff(L,D,i-1),i=1..N+1):

Eq:=sum(A[j+1]*diff(Epsilon(t),t$j),j=0..N)=0:

init:=seq((D@@j)(Epsilon)(0)=piecewise(j<>N-1,0,1/A[N+1]),j=0..N-1): E:=Heaviside(t)*rhs(dsolve({Eq,init}));

1 V3e^{( p -} 3 ^{V 3} “ ^{) t} \

12 Ш J

/ 1 V3e^{( p+} 3 ^^{ш )} ‘

E = Heaviside (t)-- ’  12 w

Полученные выражения для оператора L(D) и его элементарного решения E(t) тождественно равны выражениям, полученным ранее.

Рассмотрим также пример решения уравнения сверток с помощью системы Maple.

Пусть в уравнении

[М(t)T(t)] * и = W,

в качестве W выступает функция, график которой изображен на рисунке 1. Функцию W будем называть « выходным сигналом » .

Пусть также

М (t) = t ² ,

Т (t) = —— e ^pt sin wt

ш

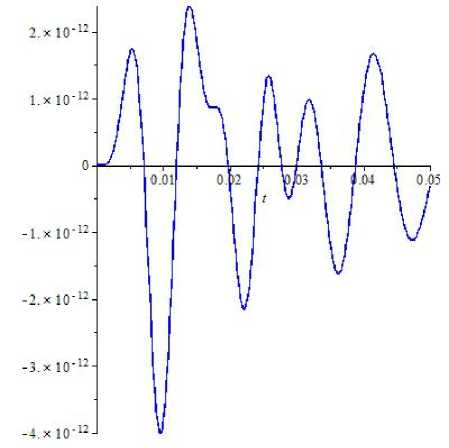
Рис. 1. График выходного сигнала решение оператора

P (D) = { (D -р) ⁽²⁾ + ш ² } , р = -200,ш = 300.

Функцию A(t) = М(t)T (t) будем называть « аппаратной функцией » .

С помощью описанного выше метода найдем решение уравнения ( 22 ), то есть неизвестную функцию U (t), которую также будем называть « входным сигналом » .

Задав значения р = -200 и ш = -300, получим элементарное решение оператора L(D):

omega:=500: p:=-200:

E;

Heaviside (t) ( — V3e^{( - 200+} 530 ^ - — V3e^{( - 200 -} 530 ^Я 6000                   6000

В силу ( 20 )

U = P_{q +}i (D)(E * W ), однако, используя свойства свертки, можно вычислить U как

U = P q ₊1 (D)(E) *W.

Найдем P q +1 (D)(E):

Pq1E:=b[1]*E:

for i from 2 to n+1 do

U1:=U1+b[i]*diff(E,t$(i-1));

end do:

Pq1E:=simplify(U1):

Здесь Pq1E — результат действия оператора P _q+1 (D) на E .

Теперь найдем решение уравнения ( 22) U = P _q+1 (D)(E) * W :

U:=simplify(int(subs(t=tau,Pq1E)*subs(t=t-tau,W),tau=-infinity..infinity));

График функции входного сигнала изображен на рисунке 2.

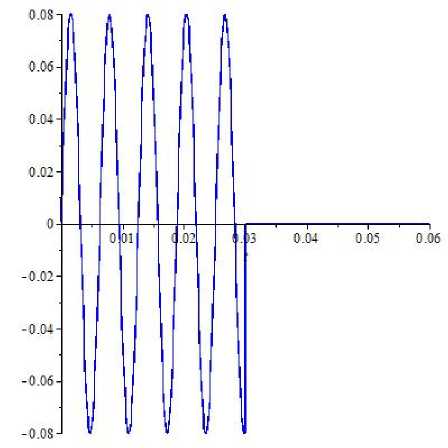
Рис. 2. График входного сигнала

• 8.    Заключение

В данной работе был исследован класс уравнений сверток вида ( 3 ) в сверточной алгебре D '+ (R). Для данного класса уравнений доказано существование и единственность решения, а также предложен метод получения решения. Кроме того, в работе приводится пример программной реализации метода решения уравнений класса ( 3 ).