Изменение характеристик рабочей поверхности шлифовального круга за период его стойкости

Введение. Процесс шлифования имеет вероятностный характер, что вызывает разброс характеристик качества обрабатываемых деталей [1–6]. В процессе шлифования поверхности резания образовывающиеся при движении режущих кромок абразивных зерен в пространстве заготовки отображаются на ее поверхности в виде микрорельефа и, следовательно, форма единичных рисок на поверхности зависит от особенностей контакта с материалом поверхности и формой абразивных зерен на рабочей поверхности шлифовального круга.

Для шлифовальных операций наиболее нестабильным элементом системы является шлифовальный круг. Следует отметить, что в 65…75 % случаев используются шлифовальные круги на керамической связке, работающие в режиме затупления [7–11], свойства которых в результате износа абразивных зерен меняются в процессе эксплуатации. Как следствие, меняются сила резания, температура в зоне обработки, шероховатость обрабатываемой поверхности и производительность обработки.

Изменение состояния рабочей поверхности шлифовального круга определяется числом режущих кромок, их формой, распределением режущих кромок на рабочей поверхности, засаливанием и т. д. По данным [3, 12–15], основным параметром процесса шлифования, оказывающим наиболее существенное влияние, является форма режущих кромок. Исследования авторов [1, 3, 8, 13–15] показали, что наиболее адекватной моделью вершины зерна является модель в виде параболоида вращения (рис. 1).

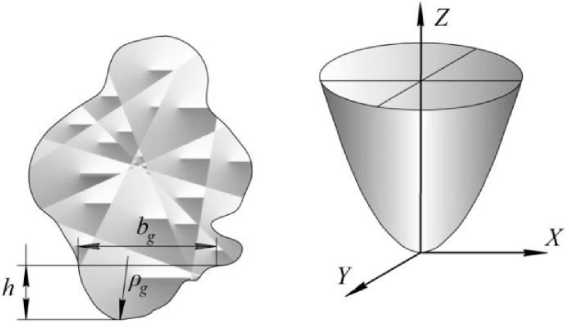
а)                                    б)

Рис. 1. Модели абразивного зерна: а – контур зерна; б – параболоид вращения

Согласно [3, 4, 15–19] расчет характеристик шероховатости поверхности, съема материала заготовки, силы резания, температуры в зоне контакта абразивного зерна с материалом заготовки можно выполнить, основываясь на ширине абразивного зерна b g и радиусе закругления его вершины p g .

В работах [3, 8, 14, 16, 18] показано, что ширину абразивного зерна bg на расстоянии h от его вершины можно определять по зависимости bg = 2,(2Pgh,                                                                            (1)

где p g – радиус округления при вершине зерна.

Для всех разновидностей форм абразивных зерен уравнение, описывающее ширину абразивного зерна b g , имеет вид (см. уравнение (2)), в котором коэффициент C b и показатель степени m необходимо определять экспериментально [3, 18–20]:

b g = C_bh m .                                                                                       (2)

Согласно [3, 14, 16–19] текущее значение коэффициента Cbτ может быть вычислено по зависимости (3), bgτ из зависимости (4), а после правки поверхности шлифовального круга плотность распределения абразивных зерен можно моделировать зависимостью z b т

= C b

v tf - u - hg )

b g т

t f - u

v tf - u - hg )

m т ,

f . ( u ) = C f U ^{x- 1}, (5) где t f – фактическая глубина резания; u – расстояние от условной наружной поверхности шлифовального круга до вершины зерна; h_τ – расстояние до рассматриваемого уровня от вершины изношенного зерна; C f и χ – коэффициент и показатель степени.

Целью статьи является изучение влияния времени работы шлифовального круга после правки на параметры состояния его рабочей поверхности и получение отдельных эмпирических коэффициентов , необходимых для численных расчетов ожидаемой шероховатости поверхности, силы резания и др.

Для экспериментальных исследований параметров рабочей поверхности инструмента применяют такие методы получения первичной информации, как царапание полированного образца, непосредственное наблюдение за режущими кромками с помощью профилографирования, оптического или электронного микроскопа. Их подробный анализ выполнен в работах [15, 18–23].

Материал и методы. В проводимых исследованиях для анализа изменения числа и распределения режущих кромок применили метод профилографирования поверхности круга, а для исследования изменения геометрии режущих кромок – метод царапания полированного образца.

Профилограммы круга снимали в направлении, перпендикулярном вектору скорости резания непосредственно на круглошлифовальном станке BUА16 (рис. 2, а ), оборудованном тензометрическими центрами (рис. 2, б ) и вибродатчиком (рис. 2, в ). Параметры ощупывающих игл соответственно равны: угол при вершине профиля – 90° и 110°, радиус округления – 2 и 3 мкм; длина вершины клина иглы – 0,43 и 0,25 мм. Скорость перемещения иглы относительно рабочей поверхности инструмента составляла 1,0 и 0,4 мм/с.

Для измерения разновысотности зерен записывали по пять участков рельефа круга длиной 15 мм каждый. На профилограмме выбирали 2…3 наиболее выступающие вершины, проводили по ним линию нулевого уровня и измеряли расстояния до других вершин зерен. Весь диапазон высоты профиля разбили на интервалы, по результатам замеров строили кривые изменения частоты режущих кромок по глубине инструмента. Для аналитического описания закона распределения режущих кромок по глубине инструмента применяли бета-распределение [1–3]. Результаты статистической проверки гипотезы о законе распределения режущих кромок кругов 24АF60L6V после 10 мин шлифования приведены в табл. 1.

При оценке изменения профиля вершины абразивных зерен шлифовальный круг прижимали к полированному образцу и проворачивали на 2...3 мм. Для снижения искажения профиля вследствие пластических деформаций образец изготовили из закаленной стали ШХ15, НRС 55...60.

a)

Рис. 2. Общий вид установки для исследования процесса шлифования: а – станок BUА16, б – тензометрические центры, в – вибродатчик

Исследование изменения состояния рабочей поверхности шлифовального круга проводилось при шлифовании стальных образцов (сталь 40Х, HRC размеры d×l = 35×60 мм) кругом 1 250×32×76, марки 24АF60L6V на режимах V к = 31,7 м/с, V д = 27 м/мин, S пр = 1,3 м/мин, S поп = 0,01 мм/дв.ход. Характеристики рабочей поверхности шлифовального круга контролировались сразу после правки и спустя 10, 20 и 30 мин работы.

Повторяемость опытов была принята равной пяти. Радиусы закругления вершин зерен в плоскости, перпендикулярной вектору скорости резания, замеряли шаблонами по профилограммам, снятым с царапин при одинаковом горизонтальном и вертикальном увеличениях. При уровне значимости 0,95 табличное значение χ ² равно 26,3. Расчетные радиусы вершины абразивных зерен рассчитывались по зависимости (1).

Величина относительного износа h 0 = 2,8 × 10^–7 мм определялась по величине размерного износа Δ R = 14,5 мкм и пути резания единичным зерном за 30 мин работы инструмента.

Для описания текущего профиля измерялась ширина царапин на различных уровнях от впадин. Результаты измерений аппроксимировали уравнениями вида b g = C b × h^m .

Таблица 1

Статистическая проверка гипотезы о законе распределения вершин зерен по глубине инструмента 1 250×32×76 марки 24АF60L6V

№ интервала i	Интервал, мкм	Частота вершин зерен m i	Расчетная вероятность попадания в интервал P i	№ интервала i	Интервал, мкм	Частота вершин зерен m i	Расчетная вероятность попадания в интервал P i
1	0–2,1	9	0,0888	11	21,0–23,1	4	0,0528
2	2,1–4,2	16	0,0972	12	23,1–25,2	8	0,0456
3	4,2–6,3	18	0,0962	13	25,2–27,3	5	0,0405
4	6,3–8,4	27	0,0923	14	27,3–29,4	4	0,0345
5	8,4–10,5	22	0,0883	15	29,4–31,5	4	0,0286
6	10,5–12,6	17	0,0830	16	31,5–33,6	3	0,0230
7	12,6–14,7	11	0,0774	17	33,6–35,7	3	0,0177
8	14,7–16,8	13	0,0714	18	35,7–37,8	2	0,0126
9	16,8–18,9	6	0,0653	19	37,8–39,9	2	0,0088
10	18,9–21,0	9	0,0591

При исследовании законов распределения режущих кромок по глубине инструмента шлифовали образцы из закаленной стали ШХ15 (НRС 55...60) на станке BUА16 кругами 1 250×32×76 марок 24АF60L6V и 24АF60N7V ( V к = 31,7 м/с, V д = 39 м/мин, S пр = 0,9 м/мин, S поп = 0,01 мм/дв.ход). Результаты экспериментов обрабатывались в программе Stata 8.0.

В табл. 2. приведены данные по коэффициенту корреляции между шириной режущей кромки и расстоянием до уровня от вершины зерна, расчетными и табличными значениями критерия для оценки коэффициента корреляции, коэффициенту пропорциональности и показателю степени уравнения регрессии, радиусу закругления при вершине зерна.

Таблица 2

Геометрия режущих кромок абразивных зерен круга 1 250×32×76 марки 24АF40K7V

Время работы инструмента, τ , мин	Коэффициент корреляции, r bi	Расчетные значения		Радиус закругления при вершине зерна p g , мкм
		C b	m	расчетный	эксперимент
0	0,78	1,13	0,65	26	26
15	0,78	1,36	0,94	78	66
30	0,73	1,48	0,64	–	–

Результаты и обсуждение. Для всех τ коэффициент корреляции значим и равен 0,7...0,8, что свидетельствует о достаточно тесной связи между b g и h g . С увеличением времени работы инструмента наблюдается закономерное увеличение ширины режущей кромки и радиуса закругления при вершине инструмента, а при работе в режиме затупления появляются почти плоские вершины. Сопоставление расчетных значений радиуса закругления с экспериментальными показывают на их достаточно хорошее соответствие.

Таким образом, проведенные исследования по износу единичных абразивных зерен круга подтверждают качественную картину износа, полученную в работах [3, 8, 15–19], и позволяют сделать заключение об адекватности зависимостей (2) и (4) реальному процессу. Результаты экспериментов по исследованию законов распределения режущих кромок абразивных зерен по глубине шлифовального круга приведены в табл. 3, 4 и на рис. 3.

Отмечается заметное изменение закона распределения режущих кромок по глубине шлифовального круга. Максимум кривых смещается по глубине шлифовального круга, частота снижается с увеличением времени его работы. Для испытанных марок кругов наибольшие изменения закона распределения наблюдаются в первые минуты работы инструмента, когда из связки вырываются и разрушаются абразивные зерна, поврежденные правкой круга. При дальнейшей работе шлифовального круга изменения в законе распределения снижаются. Об этом же свидетельствует анализ параметров распределения при моделировании участков кривых распределения, лежащих в пределах глубины резания, зависимостью [3, 12–14, 24]:

f ξ ( u ) = ^{χ u χ} _χ ¹,                                                                                            (6)

u где Hu – слой круга, в котором распределены режущие кромки (принимается равным фактической глубине резания tf).

Таблица 3

Параметры гистограмм и распределений режущих кромок абразивных зерен по глубине шлифовального круга

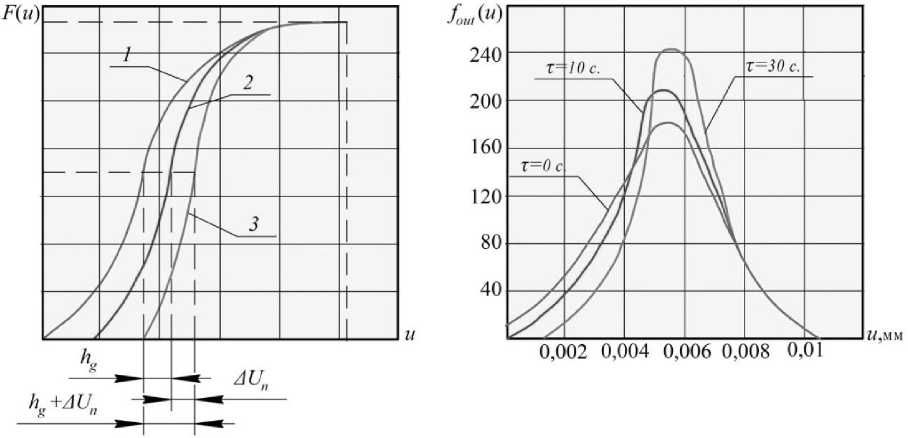
а )                                                                   б )

Рис. 3. Распределение режущих кромок абразивных зерен шлифовального круга: а – распределение по глубине; б – плотность распределения по глубине

Марка круга	Время работы инструмента τ, мин	Параметры гистограмм		Параметры бета-распределения		Показатели для проверки закона распределения
		Х	S2	η	γ	β 1	β 2
	0	0,24	0,029	2,1	1,3	0,67	3,5
24АF60K7V	4	0,28	0,040	2,3	1,2	0,51	2,7
	8	0,32	0,048	2,3	1,2	0,33	2,2
	10	0,33	0,049	2,4	1,2	0,33	2,2
	0	0,37	0,62	1,7	1,0	0,19	2,2
24АF60N7V	4	0,35	0,55	2,0	1,1	0,28	1,6
	8	0,37	0,053	2,1	1,3	0,17	2,0
	12	0,36	0,054	2,1	1,2	0,18	2,0

Таблица 4

Значение коэффициентов χ и H u в уравнении (6)

Время работы инструмента τ, с	Значение коэффициентов		Время работы инструмента τ, с	Значение коэффициентов
	χ	H u		χ	H u
0	1,49	0,012	8	1,79	0,016
1	1,79	0,016	10	1,71	0,020
4	1,7	0,016

За первую минуту работы инструмента показатель χ изменяется в 1,3 раза, за последующий период он колеблется в пределах погрешности экспериментальных данных.

Заключение. Выполненные экспериментальные исследования подтверждают вывод, что за период стойкости инструмента при работе в режиме затупления наиболее значительно изменяется форма режущих кромок. Подтверждено, что полученные различными авторами зависимости обеспечивают достаточно полное описание рабочей поверхности инструмента, соответствуют реальному процессу и могут использоваться для прогнозирования показателей процесса шлифования и разработке оптимизационных моделей. Для кругов марок 24АF60L6V и 24АF60N7V получены эмпирические коэффициенты, необходимые для выполнения численных расчетов ширины и радиуса округления абразивного зерна.