Явная схема решения третьей смешанной задачи для квазилинейного уравнения теплопроводности

В настоящей работе используются идеи, изложенные в работах [1, 2], в которых была предложена и обоснована явная устойчивая схема для линейного уравнения теплопроводности.

1. Численный метод

Рассмотрим следующую постановку третьей смешанной задачи для одномерного однородного квазилинейного уравнения [3]:

с ( u ) | т =д ( q ( u ) | u ) ,        0 <  t <  t , 0 <  x <  l , д t   д x V    д x ) u ( x , 0) = ^ ( x ), -f q ( u ) | u )    = A i ( u (0, t )) ( 9 i - u (0, t ) ) + Q i ,                               (1) V     д x V x = 0

( q ( u ) )    = A r ( u ( L, t )) 9 - u ( L, t ) ) + Q r ,

[V     dx ) x=L где u = u (x, t) - температура стержня; 0 < x < L - координата; 0 < t < T - время; L - длина стержня; T - конечный момент времени; с(u) - объемная теплоемкость материала стержня; q(u) - теплопроводность материала стержня; ^(x) - функция начального распределения температуры стержня; Ai (u) - коэффициент теплоотдачи на левом конце стержня; Ar (u) - коэффициент теплоотдачи на правом конце стержня; 91 - температура внешней среды на левом конце стержня; 9r - температура внешней среды на правом конце стержня; Qi = Qi (t) - мощность потока тепла на левом конце стержня; Qr = Qr (t) - мощность потока тепла на правом конце стержня. Функции c = с(u), q = q(u), Ai = Ai (u) и Ar = Ar (u) предполагаются непрерывными функциями температуры, заданными для всех значений температуры.

Замена искомой функции

Поскольку в уравнении присутствует член q (u)   , то удобно сделать замену дx u                                               д G       д2 G q (u) c (u)

G ( u ) = q ( g ) d q . Тогда для функции G получим уравнение — = a ( u )—— , где a ( u ) = 0                                                               д t          д x ²

Хайрисламов М.З., Явная схема решения третьей смешанной задачи Геренштейн A.B. для квазилинейного уравнения теплопроводности коэффициент температуропроводности. Функция G ( и ) является строго монотонной функцией температуры, поэтому обратная функция G ¹ существует и может быть вычислена в конкретной точке, например, методом дихотомии.

Шаблон схемы. Расчетные формулы

На плоскости ( x , t ) используется равномерная сетка [2]

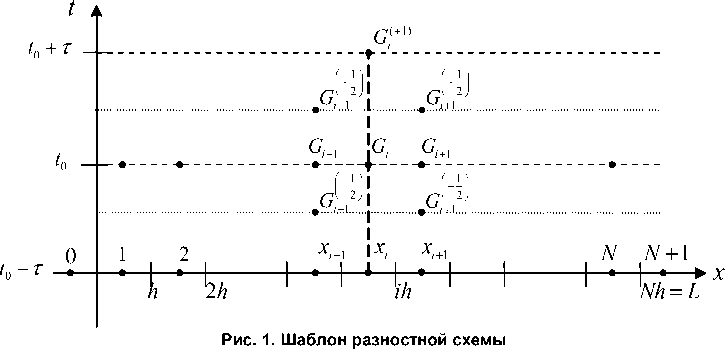
to = toh х юТ, toh = Jx= I i -i]h, i = 1,2,..., n!> , toT = {tj = jT, j = 0,1,...}, I V 2)                  J где h = LN - шаг по переменной x, T - шаг по переменной t. Шаблон предлагаемой схемы представлен на рис. 1. Для обозначения значений сеточной аппроксимации функции G на следующем временном слое используется верхний индекс (+1), на следующем полуцелом времен-

Г. 1

ном слое - I +— I , а на предыдущем полуцелом временном слое -

Используемая расчетная формула имеет вид

^^^^^^^.

.

- 2 a ² ( U i ) _t

G<+0 = (G - в)e h2   + at + в,

где

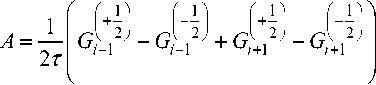
B = G - 1 ⁺ G + 1 - _A.J?  .

2           2 a ²( u i )

Для расчета значений функции G на временном слое t = T , а также ний функции в полуцелых слоях по времени используются формулы:

для вычисления значе-

- ^{2 a 2} ( и )

G ( t ) = Ge ^{h 2}

2 a ² ( u i )

1 - e h h

Г 1 )             a ² ( U i )

G i ^{- 1 +} G^{i + 1} , g X ²J = G i e h ²

1 - e

a ² ( u_t )

G - 1 ⁺

■^.(3)

Для выполнения краевых условий введены фиктивные узлы с номерами 0 и N + 1 (см. рис. 1): сначала рассчитываются значения искомой функции во внутренних точках, после чего, исходя из краевых условий, задаются ее значения в фиктивных узлах.

Используя следующие аппроксимации второго порядка точности

2 ( U (0, t )) = ^{3( 2 1} > 1 " ² ) 2 , q ( U (0, t )) = ^ q LZ q ., a u ^O^ t ) = u ^^ u o , u (0, t ) = u o^ u ! ,

2                     2       дx       h2

нетрудно получить формулу определения температуры в фиктивном узле 0:

U 1 ^{Г 3} q ¹f q ² - ^{3( 2 1} ) 1 7 ( ^{2 l} ) ² 1 + (3( 2 / ) 1 - ( 2 1 ) 2 )6' i + 2 Q i

V h           2

u ⁰ =                  3 4 1 - q 2 ₊ 3( 2 1 ) 1 - ( 2 1 j;

h2

Краткие сообщени^

Аналогичные рассуждения для правого конца приводят к расчетной формуле для узла N + 1

„ | ³ q N - ^qN - 1    ^{3( Л} г ) N - ^{( Л} г ) N - 1 ]

иN I ,---~-------- I+ (3(Лг )N - (Лг )N-1)Уг + 2Qr

V h              2 J

N ^{+ 1                     3} q N - q N - 1 + ^{3( Л} г ) N - ^{( Л} г ) N - 1

h              2

• 2.    Тестовая задача

С учетом конечности скорости распространения тепла в [4] были получены приближенные решения одномерной задачи нелинейной теплопроводности на полубесконечной прямой при заданном потоке в начале координат в виде степенной зависимости. В данной работе с использованием идей, изложенных в [4, 5], получено аналитическое решение следующей третьей смешанной задачи на полубесконечной прямой для одномерного квазилинейного уравнения теплопро- ле координат.

В частности, при n = 2 точное решение задачи (6)-(8) будет таким:

и ( x , t ) =

_< 42 a ( a t - x ),

x <  a t , x >  a t ,

где a =

-Л + V Л + 272 Q 2

водности: Uи   U ( nUи । — = — un— ,         t > 0, x > 0,                       (6) U t   Ux V   Ux J ’                  ,       , и (x, 0) = 0,                   x > 0,                                 (7) I un |u)    = Ли\х=0 - Qtn, t > 0,                               (8) V   Ux J x=0 где n > 0 - показатель степени, характеризующий лучистую теплопроводность, Л > 0 - коэффициент теплоотдачи, Q > 0 - коэффициент, характеризующий мощность теплового потока в нача-

Pиc. 2. Численное и точное решени^ за^ачи в разные моменты времени

Полученные результаты позволяют говорить о хороших свойствах предложенного численного метода.

Хайрисламов М.З., Геренштейн A.B.

Явная схема решения третьей смешанной задачи для квазилинейного уравнения теплопроводности