Явное представление сокращенных в размерности уравнений Эйлера сжимаемой жидкости и полной системы уравнений гидродинамики в интегральной форме

DOI:

На сегодняшний день прямое численное моделирование процессов горения, обтекания, развития гидродинамических неустойчивостей, турбулентности, а также многих других гидродинамических явлений по ряду причин вычислительного характера невозможно или чрезвычайно затруднено [8–10; 13; 14; 17; 20]. Большой интерес представляют различные способы сведения полной системы гидродинамических уравнений и химической кинетики по объему к уравнению или системе уравнений на поверхности, приводящие к уменьшению вычислительных мощностей [4; 5]. В теории горения, в частности, поставленную задачу можно было бы существенно упростить, если бы удалось свести полную систему уравнений гидродинамики горения к единственному уравнению, описывающему положение фронта реакции [16; 19]. Научный интерес также представляет подобная процедура для получения описания поверхностей других гидродинамических разрывов [8], например, тангенциального разрыва, который встречается в струях, следах от летящего тела или на поверхности воды в виде ветровых волн, а также является одним из препятствий, стоящих на пути осуществления управляемого инерциального термоядерного синтеза [2; 11; 12]. В частности, необходимо учитывать динамику тангенциального разрыва при описании гидродинамических неустойчивостей (Релея — Тейлора, Дарье — Ландау, Мешкова — Рихтмайера, Кельвина — Гельмгольца), гравитационных волн и ряда других явлений [8]. Данный метод позволяет также рассчитать гидродинамические разрывы с учетом вязкости, образования звука и других изменений плотности газов и жидкостей, пользуясь информацией только на их поверхностях. В общем случае решение нелинейной задачи описания тангенциального разрыва не найдено. Аналитическое решение может быть получено лишь в двух предельных случаях для бесконечно тонких пленок и в приближении «опрокинутой мелкой воды» [15; 18].

В данной работе мы сводим нестационарные уравнения Эйлера сжимаемой жидкости и полную систему уравнений гидродинамики к «стационарным» интегро-дифференциальным уравнениям, у которых производные по времени отсутствуют. С помощью этих уравнений гидродинамические разрывы могут «видеть» весь внешний поток в реальном времени. А именно, если есть система уравнений движения разрыва, то, вычисляя движение самого разрыва, а также других величин на его поверхности, можно сразу вычислить весь внешний поток без привязки ко времени. Все сокращенные в размерности уравнения получены в явном виде, в отличие от предыдущих работ авторов [1; 3], где предлагались до 200–500 уравнений с сокращенной размерностью, которые очень сложно исследовать и моделировать.

В работе авторов [7] нестационарные уравнения Эйлера несжимаемой жидкости и Навье — Стокса с постоянной плотностью сводятся к «стационарным» интегро-дифференциальным уравнениям, у которых производные по времени отсутствуют. Однако системы уравнений, приведенные в данной статье, к ним формально не сводятся, потому что здесь используется другой способ переопределения и учитывается существенным образом функция зависимости давления от плотности жидкости.

1.    Уравнения Эйлера сжимаемой жидкости в изоэнтропическом 3D-потоке

В изоэнтропическом 3D потоке, если плотность p ( r ,t) = const , но s( r ,t) = const , где s( r , t) — энтропия жидкости, то есть существует однозначная связь между давлением Р ( r , t) и плотностью p ( r , t) : Р = Р д ( р ) , уравнения Эйлера примут вид [8]:

IS ^{+ (u V )u +} ^Вь Т ^Vp = ^{0,                     (1)}

ш = V х u ,

д р

— + u • Vp + р div u = 0, dt где V = (di, dd, dd); u(r,t) — скорость жидкости в точке r = (x, y,z) в момент време ни t; u = uo(r).

t —o

Взаимно-однозначно перейдем к лагранжевым переменным начального положения частиц газа и времени r _o , t (то есть к разметке).

— = u(r,t), r = r(ro.t) и ro = ro(r, t), ro _ = r, r = ro.

tit                                                          t—0

Тогда из системы уравнений (1)–(3) следует, что [4]

u • V r o = W o ( p o ) p          p o ( r o ) ,

1 d (xo,yo,zo) = p 9(x,y,z)      po(ro)’ где po(r) и cuo = V х uo — начальные данные у p(r,t) и си = V х u при t = 0. Из (5), (6) получаем

u(ro,t) = uo(ro) • Vor p              po(ro), где Vo = (ddo, d|0, dd0).

Пусть мы имеем поток u ( r ,t) во всем объеме и достаточно быстро убывающий на бесконечности. Тогда выражение для скорости u может быть записано в виде [14]:

u = —V r х 4 п

/

w ( r ' , t ) | r — r ' |

d³ r' + -1- V_r

4 n ^r

/

div u ( r ' , t ) | r — r ‘ |

d ³ r ' =

¹ [ ^{(r — r} ' ) ^х ^ ^(r ‘ ^,t) _d 3 r ‘ - 1 [ ( r — rOdiv u ^ r^t ) _d3r 4n J        | r — r ' | ³                4n J        | r — r ‘|³

где Vr = (^, ^, ^). Перейдем в подынтегральном выражении в формуле (8) к пере-охоуиг менным Лагранжа (4), используя (6), (7):

_    1 Г (Г — r'(r0,t)) х Ш(г0,<) a r'  3 ‘     1  Г (Г — r'(r0,t)) • div u(r0,^ dr’

4nJ       |r — r'(r0,t)|3       Э r0    0    4nJ        |r — r'(r0,t)|3        dr0

= — ± /(r — rK х (^^^)  —  /(r—r^W

4n             0   /        |r — r' (r0,t)|3         0    4nj       |r — r' (r0,t)|30

где

‘ ,x = ^д М^^уУ) , a ⁽ x',u _y ( ry^' )    a ⁽ ^,y',u _z ^(r 0 ^,t))

'

0,              дr0                   дr0

Используя определение переменных Лагранжа (4), находим

/          d r               1 /7 ,                      (^W0 ^(r 0 ⁾-Vc)^r ' ^(r 0,^t),_3/

^u(r 0 ,^t) = dt^(r 0 ,^t) = ^— 4п/(rM ^{— r (r} 0 ,^t)) ^х₁ r ( r o;7) -P ( r o;7)F ^d r 0 ^—

1 r( ^r(r 0 ^{,t) — r} ' ^(r 0 ^,t) ) ^M(r 0 ^,t) ₃ ‘

4nj       | r ( r 0 ,t) — r ' ( r 0 ,t) | ³          r ⁰ '

Продифференцируем выражения (10) по лагранжеву времени t . Тогда, используя уравнения Эйлера (1)–(3), получим некоторые интегральные выражения вида

9P _S ( р ) рд р

^Vp = at ^(r ° ,^<) =

4 п

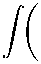
д at г(гМ)

^— il^r ' ( r ⁰ ,*))

^(w 0 ^(r 0 ⁾ • ^V 0 ^)r ' ^(r 0 ^,t) _d 3 r '

Н^,^ ^— r ' ^(r 0 ^{,t) | 3}     0

^ /(^r(r ° ,^t)

^{— r} ' ^(r 0 ^,t))

х

( W 0 ( r 0 ) .V 0 )g r ' ( r 0 ,t)     +

^{| r(r} 0 ^{,t) — r} ' ^(r 0 ^{,t) | 3       0}

+4 П / ( ^r(r 0 ^{,t) —} r ' ^(r 0 ^,t) )^х

х

/ ^{( w} 0 ^(r 0 ⁾ • V 0 ^)r ' ^(r 0 ^,t)

^{| r(r} 0 ^{,t) —} r ' ^(r 0 ^{,t) | 5}

( ^r(r 0 ^,t)

^{— r} 'H,^) • ^ ^r(r 0 ^,t)

— a r ^{(r 0} ,^f)

^d 3 r 0 ^—

J_ [ (| r ( r o _L^)^-| ^^ r ( r 0 ₁^⁾)^(r ^ _L^)_d 3 ' — J_ r ( r ( r 0 ,t) — r ' ( r 0 ,t)) gg^ _d 3 ' , 4nJ          | r ( r 0 ,t) — r ' ( r 0 ,t) | ^{3             Г}0     4n J      | r ( r 0 ,t) — r ' ( r 0 ,t) | ^{3        Г}0

+Ы

^(r(r 0 ^{,t) —} r ' (^^W ^(r 0 ^,t) H^)^— r ' ^(r 0 ^{,t) | 5}

(^0,^

^{— r} ' ^(r 0 ^,t) ) • (;^dt^r(r 0 ^,t)

— s^r ' ^(r 0 ,^f)

^d 3 ^r 0 ,

где

дМ (^,t)   ^д (дt ^{M ж (г} o ,^t),^у ,^z

дt

^{д г} 0

')   ^д^u_ж^(г0^,t), Д у ' ^(го^,t),z') , ^д (и^^^у',

^{д г} 0

+

+

^д (^з^о^Н у (то,^')

дго д (6х' (го, t),y',uz (г0,t)

+

^д (^х‘, It^

д г о

+

дго д (V 8 у' (го^),м

^{( r} 0 ^{,t ) ,z} ')    ^д ^U _y( r o ,^,

д г _о

It^z' ^(го^) ^дго           ⁺

It ^z' ^(г 0 ^,t) ) ------- +

Перепишем выражение (6)

в

виде

д г о

. _z ( r o ,г)    ^д (

^х,У ^ ^(г 0 ,^t

д г о

.

д (х,y,z) = р ( г о ) д (х o ,y o ,z o )       р

.

Используя (12), находим, что компоненты вектора градиента плотности ∇ρ в формулах (11) в переменных Лагранжа (4) выражаются следующим образом дР = д (р,y,z) дх д (х,y,z)

^{1        д (}р ^, y ^, z⁾

р     д ( р ,y,z)

-qd^^L д (х о ,у о ,^ о )     Р о ( г о ) д(х о ,У о ,^ о )'

8 ( х о ,г_го,г о )

Аналогично получаем, что

д р ^д У д р дz

р     д(х, р ,z)

Р о ( г о ) д(х o ,y o ,z o ) ’ р     д(х,у, р )

Р о ( г о ) д(х o ,y o ,z o ) '

Таким образом, формально в переменных Лагранжа мы получили систему из 13 интегро-дифференциальных уравнений (10)-(12) и 13 неизвестных функций г ( г ₀ ,t) , р ( г ₀ ,t) , u ( г ₀ ,t) , д u ( г ₀ ,t)/дt и д г ( г ₀ ,t)/дt , где производная по времени от этих неизвестных отсутствует в явном виде. Условие ш _о ( г _о ) = 0 здесь существенно (в противном случае, уравнения (8)–(10) превратятся в верные тождества, и никакого переопределения при этом нет), то есть потенциальное решение этим методом найти невозможно.

Если мы в уравнении (11) в левую часть поставим дu(г0,t)/дt = д2г(г0,t)/дt2, в правую часть дu(г0,t)/дt = -VF/р = —^р/р)дР5(р)/др и u(г0,t) = дг(г0,t)/дt, то с учетом (12)–(15) получим систему из трех интегро-дифференциальных уравнений для определения лагранжевых координат г(г0,t), где старшие производные по времени выражены уравнения условиями

через остальные, а значит и всего потока. Формально тогда интегральные (11) в переменных Лагранжа определяют эволюцию потока (с начальными

r

_t_₀ = г о , д г ( г о ,t)/дt

= u ₀ ( г ₀ ,t) ) и являются следствиями уравнений

Эйлера (1)–(3).

В случае, если имеются границы у потока, то выражения (8), (9) несколько усложняются [14], но уравнения, аналогичные (10)–(12), также можно получить.

Фактически, чтобы редуцировать уравнения Эйлера (1)–(3), достаточно использовать только одно из уравнений (8). Для этого нужно применить прием сокращения размерности (редукции) в переопределенных системах УрЧП [6], обобщенный очевидным образом на случай интегро-дифференциальных уравнений.

2.    Полная система нестационарных уравнений гидродинамики в 3D-потоке

Рассмотрим уравнения гидродинамики в 3D-пространстве в виде [8]:

др дт + div(pu) = 0, (16) дu  , „.   VP  дu         „/u2\  VP  Vo  F ^t + (uV>u + v = gt - U x ш + V(^yj+   = - + р, (17) ш = V x u, (18) Г дs ,       , "I рТ дт + (uV)s =Q - div q + Ф, (19) T = T (p,s), P = P (p,s), (20) m    VP Vw = T •Vs +--, (21) ρ где р, u, P, Т, w и s — плотность, скорость, давление, температура, удельная тепловая функция и энтропия (на единицу массы) рассматриваемой среды соответственно. Здесь F, Q — объемные сила и тепловыделение; q = -XVT — тепловой поток ( Л — теплопроводность); σ — тензор вязких напряжений, для которого имеем

V o =

5 (^Д и ⁺ 3 V ( V u )) ’

где µ — сдвиговая динамическая вязкость. Входящая в уравнение (19) диссипативная функции Ф равна

Ф =

5 Е( к,г=1 х

ди _г ди _k дх _k дх _г

ди

дx k

У - 2 5 Е ( У ,

У 3 VxzV

где (и 1 ,и 2 ,и з ) = (u _x ,U y ,u _z ) , (х х ,Х 2 ,Х з ) = (x,y,z) .

Уравнения (20) и (21) — термодинамические соотношения, которые зависят от свойств рассматриваемой среды.

Введем «поправку» a ( r ,t) к вектору u ( r ,t) и «псевдоплотность» р • ( r , t) , которые определим из уравнений:

д р ^

-дг + (u + a) •Vp + р div(u + а) = 0,

+ ((и + a)V) a + (aV)u + Т •Vs + — + — = 0.

дт р р

Почленно сложим формулы (17) и (25). Тогда, учитывая (21), находим, что д (u + a)   z. .„ g—- + ((u + a)V) (u + а) + Vw = и + a дт

- (u + a) x (ш + V x a) + V ^(u ^^ a) ^ + Vw =0.

Векторное поле u + а формально можно рассмотреть, как эйлеров изоэнтропический поток с плотностью P^(r,t) и энтальпией w(r,t). Взяв операцию «Vx» от обеих частей (26), находим, что д(ш +V Х а) = V x [(u + а) x (ш + V x а)] .              (27)

Перейдем к псевдолагранжевым переменным начального положения частиц газа и времени r _o , t (то есть к разметке).

d r

— = u ( r , t) + а ( г , t),   r = r ( r o , t)  и   r o = r o ( r , t),   r o

,r t=0

= r 0 . t =o

Тогда уравнения (24) и (27) можно преобразовать к виду [4]:

( ш + V x а ) • V r o = ( Ш о ( г о ) + V x а o ( r o ))

P ^e                           P ^e o ( r o )

1 d (x o ,y o ,z o ) =     1

Pe д(x,y,z)      Peo(ro), где а0, p^o, ш0 = V x uo — начальные распределения величин а, p^, ш, u = uo(r). Положим здесь а0 = 0 и peg = po. Тогда, как было показано, уравнения (29)-(30) можно преобразовать к виду (5), (6), а сама формула (30) принимает вид

P o ( r o ) = д (x,y,z )

P ^e        д (x o ,y o ,z o ).

Из (29), (30) получаем

ш ( r o ,t) = Ш o ( r o ) • V o r

P ^e              P o ( r o )

где ^V o = (^ , 5^ 0, &) .

Пусть мы имеем поток u ( r , t) + a ( r , t) во всем пространстве и достаточно быстро убывающий на бесконечности. Аналогично (8) выражение для u + а может быть записано в виде [14]:

u + а = 1 V r x [ ^{ш + Vx а} ' - d3 r ‘ + 1 V r [ ^dlv( u ^{+ а )ХХ} d3 r ‘ ,    (33)

4n                  |r — r‘|                4n             |r — r‘| где Vr = (,  ,  ). Перейдем в подынтегральном выражении в формуле (33) к пере- и.Г. ин О'^1

менным (28), используя (31), (32):

/ _{w х}    d r                1                                ( ш _o ( r 0 ) •V o ) r ‘ ( r o ,t) о .

u ^{+ а} = ( u ^{+ a})(^r o ,^t) = dt ⁽w)= ^— -J (^r(W) ^{— r}(^r o ,«)) ^x | r ₍ r ₀ , t) — r ‘ ( r _o , t) | 3 ^dr o -

_ 1 [ ^(r(r o ^{,t) — r}‘ ^{( r}' o^{,t ))}M (^ 3

4nJ       | r ( r o ,t) — r ‘ ( r o ,t) | ^{3          o} ,                              ( ⁴

где

‘ n _ ^d((« ^{+ a}M ^r o ,^t), y',^z'^}  ,  ^{д (х} ‘ , ^{( m + a )} y ^(r o ,^t), ^z ‘)  ,   ^d(x ‘ , y‘, ^{(м + а )} _г ^(r o ,^t))

.

^{M (r o ,t)}=          d r _o           ⁺          д r _o           ⁺          д r _o

Продифференцируем выражения (34) по псевдолагранжеву времени t . Тогда получим некоторые интегральные выражения вида

⁹⁽ u ⁺ ^r^ = I (r ( r o .t). ^ , ( u + a )( r o ,t), ^д( u ^{+ a} > ^{( r 0} ' ^t) ) .    (35)

Используя уравнения (26), получим, что д (u + a)(ro.t)    a2r(ro.t)

------at------= d .     = ^{-V w( p} .^s)'                    ⁽³⁶⁾

Из уравнений (16), (19), (25) и (26) следует, что д p(ro. t) at

— a V p + p div u = 0.

pT [ ^9s( d ° . ^t) — a Vsl = Q — div q + Ф.

''"/ + vu + T •Vs + ^ + F =0

at                          p p д u(ro.t)                  д a(ro.t)

= ^{— m( p} .^{s) —} St—

В выражениях для пространственных производных в (37)–(40) аналогично (12)– (15) можно перейти к псевдолагранжевым переменным (28).

Если выражения (36) подставить в интегральные уравнения (35), то вместе с уравнениями (34) мы будем иметь 9 «стационарных» интегро-дифференциальных уравнений от 14 неизвестных функций r ( r _o .t) , p ( r _o .t) , s( r _o .t) , u ( r _o .t) , a ( r _o .t) и d r ( r _o .t)/dt , где производная по времени от этих неизвестных отсутствует в явном виде. Чтобы получить недостающие уравнения, проделаем следующую процедуру. Подставим формулы (36) в уравнения (35) и продифференцируем их по псевдолагранжеву времени t . Выражения для производных d ² r ( r _o . t)/dt ² , д p ( r _o .t)/dt , ds( r _o .t)/dt подставим из формул (36)–(38). Получим три новых интегральных уравнений вида (35) и проделаем эту процедуру еще раз, используя выражения (39), (40) для d a ( r _o .t)/dt и д u ( r _o .t)/dt . В результате получим еще 6 интегро-дифференциальных уравнений вида (35), и вместе с уже имеющимися 9 уравнениями (34), (35) можно составить систему из 15 «стационарных» уравнений от 14 неизвестных функций r ( r _o .t) , p ( r _o .t) , s( r _o .t) , u ( r _o .t) , a ( r _o .t) и д r ( r _o . t)/dt .

Эта система уравнений должна допускать параметрическое семейство решений (зависимость от времени t ). Каждое конкретное решение должно выделяться данными на некоторой поверхности, которые должны быть найдены независимо.

В двумерном случае эта система уравнений будет несколько проще. Выражение (35) можно дифференцировать по времени еще раз и получать новые соотношения. Однако не все они могут быть независимыми. Достаточно продифференцировать уравнения (35) ограниченное число раз, и при выполнение некоторого условия (см. приложение А) все последующие соотношения будут следствиями ранее полученных уравнений. Заметим, что уравнения гидродинамики (16)–(21) можно редуцировать и не используя замену переменных вида (28), а ограничившись только переменными Лагранжа (4). Для редукции мы используем только то, что в новых переменных производная от завихренности по времени в соотношениях (8) или (33) выражалась через пространственные производные от остальных функций. Фактически мы предлагаем новый способ переопределения любой системы уравнений типа (16)–(21) с помощью общего интегрального соотношения по пространству [14].

Заключение

Сокращение размерности в уравнениях гидродинамики является важной задачей, которая позволяет упростить расчеты гидродинамических потоков. В целом в приложениях при конструировании двигателей внутреннего сгорания, ракетных двигателей, газовых турбин и др. данное исследование необходимо для снижения вычислительных мощностей, затрачиваемых для решения этих задач в настоящее время. В частности, снижение размерности может позволить сократить продолжительность таких расчетов на один или несколько порядков. Снижение размерности также может быть использовано, чтобы верифицировать полные расчеты гидродинамических потоков, используя упрощенные расчеты на основе результатов, полученных в данной работе, как тестовые.

В данной работе мы получили «стационарные» системы интегро-дифференциальных уравнений, которые являются следствиями нестационарных уравнений Эйлера сжимаемой жидкости (часть 1) и полной системы уравнений гидродинамики в неограниченном пространстве (часть 2). Обратное показывается на примере уравнений Эйлера (приложение А). Если к ним задать корректную задачу, то мы можем определить весь нестационарный поток в объеме без решения нестационарной задачи. Достаточно задать изменяющиеся во времени данные только на некоторой поверхности этого потока, которые должны быть определены независимо. Например, из расчета другой задачи, описывающей эволюцию жидкости на этой поверхности в терминах самой поверхности. Начальные данные задачи Коши для всего потока в неограниченном пространстве учитываются в самих редуцированных уравнениях (см. (5), (6)).

Получены также интегральные нестационарные уравнения в новых переменных (лагранжевых (4) и псевдолагранжевых (28)), которые определяют эволюцию потока.

В статье также предлагается новый способ переопределения любой системы УрЧП типа (16)–(21) с помощью общего интегрального соотношения по пространству, следующего из теоремы разложения Гельмгольца [14].

Поскольку в системах (11) и (34)–(36) есть интегрирование по пространству, то редукция по пространственным переменным данным методом невозможна.

Приложение А. Достаточные условия корректности редуцированной системы интегро-дифференциальных уравнений

Рассмотрим систему из 13 интегро-дифференциальных уравнений (10)–(12). Выражение (10) можно дифференцировать по времени еще раз и получать новые соотношения и соответственно получать новые уравнения помимо (10)–(12). Найдем условия, при которых из этих редуцированных уравнений будут прямо следовать уравнения Эйлера (1)–(3).

Продифференцируем по лагранжеву времени t первое равенство в уравнении (10).

Тогда

2 ( r o ,t) =      ( r o ,t).                                     (A.1) dt          dt 2

Аналогично продифференцируем по лагранжеву времени уравнение (12). Тогда

d( 1 ,y,z) + d(x, ^ ,z ) + d ( x, y, 1 ) = — p o ( r o ) d p             -A 2) d (x o ,y o ,z o )    d(x o ,y o ,z o )    d (x o ,y o ,z o )        p 2 dt'                '

Аналогично продифференцируем левое равенство в уравнении (11). Имеем,

1   dPs(p)    d2PS(p) dp      dPs(p) dVp   d2u p2y  dp     p  dp2  -w Vp     pdp   dt = dt2 (r°,<),        (A'3) где

1 d p d (p,y,z) + d⁽^ ,y,z) + 9⁽p, ^,z ) + ^{d (}p,y, ^ ) p dt d(x o ,y o ,z o )    d(x o ,y o ,z o )    d(x o ,y o ,z o )    d(x o ,y o ,zo)

^d W =    p      1 d p d(x, p ,z) ₊ 9 ⁽§, p,z) + 9⁽x, % , z) + 9⁽x, p , §)

^{dt     p} o ⁽ r o )     p 9t 9(x o ,y o ,z o )    d(x o ,y o ,z o )    d(x o ,y o ,z o )    d (x o ,y o ,z o )

1 d p d(x,y, p ) + ^{d (}d;,y, p) + 9^{( x} , §, p ) + ^{d ( x,} y, § ) p dt d(x o ,y o ,z o )    d (x o ,y o ,z o )    d(x o ,y o ,z o )    d (x o ,y o ,z o )

Обозначим r = r ( r _o , t) , r ‘ = r ‘ ( r 0 ,t) . Продифференцируем теперь правое равенство в уравнении (11). Получим

^ М" /(Ei + E,)A'o,             (A.4)

где

—

E =

—

(

д ²

---r dt2

—

+ 6

r—

r ‘) X

d 2 r)

д

—r dt

—

X

dt

( ^ o ( r 0 ) •W o )

| r

—

( ^ о ( г О ) • W o ) r ‘

dt dt ²

r ‘ | 3

+ 3( r — r ‘ ) X

^{| r}

X

—

r ‘ | 3

—

²( r dt

( ^ o ( r 0 ) • W o ) r ‘

| r

—

r ‘ | 5

—

• -    r‘) dt

^{(r — r} ‘ ) • (

д

X

—r dt

+ 6 ( r

—

r ‘) X

( ^ o ( r 0 ) • W o )

r‘ dt

| r

—

⁽ w o ^(r 0 ) •V o ) d^t r ‘

—

dt

^{| r}

—

—

^{(r — r}‘) ^

r ‘ | 3

д

—r dt

—

+

• -    r‘) dt

+

( ^ o ( r 0 ) •V r ‘

| r — r ‘ | 5

r ‘ | 5

^{— r} ‘ ) •

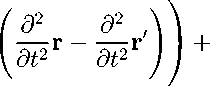
+ 3( r — r ‘ ) X

( ^ o ( r 0 ) •V r ‘

| r — r ‘ | 5

d

—r dt

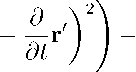
— 15( r — r ‘ ) X

( ^^ ( r O l^V oX | r — r ‘ I⁷

(^{( r — r} ' > • ( ^{r —}

-

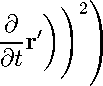
d 2 М ( — 0 ,t)

dt ²

^{(— -}

E 2 =--

+6

d

—r dt

-

.(

d r dt

-

+ 6

_— ‘ ) ^d 2 ^{м (—} 0 ^,t)    ^

-

| r - r ^′ | ³

d ^r ‘

2_—‘ ⁾ дм( r 0 ,t) dt

| r - r ^′ | ³

dt

d ²

—-r dt ²

d

—r dt

| r - r ^′ | ⁵

( r

+ 3(-

( — — — ‘ ) ^( r — — ‘ ) • ^

-

-

^2 rj ^М( r 0 ,t)

| r - r ^′ | ³

7 r‘ dt

^{— r} ‘ ^)M(- 0 ^,t) A £_— | - — — ‘ | 5       \dt

d r dt

-

| r - r ^′ | ⁵

-

+

-

I -‘ dt

ЭМ ( r 0 ,^t)

dt

+ з( --г ‘ )М( - _! .«)( - — - ‘ ) V

| r - r ^′ | ⁵

d ²

Г dt2

-

--)

-

Sr' ) ² + dt /

+

—    (^- - ^- ‘ )Л/(^{- 0} ,t ) Л- — - , ) • /

| r - r ^′ | ⁷

d

—r dt

-

d , г dt

;

d -o( dt ^{2 (r 0 ,t)}^’^ ⁺ d r o(^M " ^(r 0 ’^t)’ dt^ ^ ⁺ d r ’C ''^ '^¹ dt2 ) ⁺

_{+ 2}A  ^_r‘ t) ^-   + 2- r‘ y‘      + ^d—L (r‘ t) ^ —

^{+ 2} d r 0    dt ^(r 0 ¹⁾¹ dt^{,z   +2} d r 0    dt ^(r 0 ^,)vy,dt ⁺² d - o ^{M $ (r 0 ,t)}’dt, dt ⁺

⁺ d - o ( di^^{,M y (r} 0 ’^t),y ) ⁺ d - o ( ^ ' ’^/^(r 0 ’^{t) ,y}) ⁺ d - o ( ^ ‘ ’^{M y (r 0 ,t)}’dt ² ) ⁺

+2   (d^' ,d? (-0 ,t),^ ‘^+2   (y-d^ (-o,t), d^r)+2   (d^' мУ (-0,^)+ d—0 dt dt                d—0 \    dt        dt       d—0 dt            dt

⁺d — o ( dt^{2 ,}^ ' ^{,И г (- 0 ,t)} ) ⁺ d -^ ' ¹ df ^{,M z (- 0 ,t)} ) ⁺ d — o ( ^ ‘ ^,^ ‘ ^,^F ^{(- 0 ,t)} ) ⁺

'2,К"7‘......-) '2,1, (-,*,7.—0-..) 12,77.-d>V")-

В итоге мы имеем переопределенную систему из 23 интегро-дифференциальных уравнений в объеме (10)-(12), (А.1)-(А.4) от 20 неизвестных функций —(—,. t), p(r0,t), u(r0,t), du(r0,t)/dt, dr(r0,t)/dt, dp(r0,t)/dt, d2u(r0,t)/dt2, d2r(r0, t)/dt2, где произ- водная по времени от этих неизвестных отсутствует в явном виде.

Пусть система уравнений (10)–(12), (А.1)–(А.4) допускает некоторое параметрическое семейство решений r(r0,t), p(r0,t), u(r0,t), du(r0,t)/dt, dr(r0,t)/dt, dp(r0,t)/dt, d2u(r0, t)/dt2, d2r(r0,t)/dt2, где t E [0.T], T > 0, параметр такой, что r(r0,t)

= — 0 , t =0

д г ( г 0 -‘ ) /8‘ = u o ( r o ) . Рассмотрим r ( r 0 -t) , p ( r o ,t) , u ( r o -1) , д u ( r o -‘)/д‘ , 8 г ( г 0 -‘ ) /8‘ , д p ( r ₀ ,t)/dt , д 2 u ( r ₀ , t)/dt ² , д ² r ( r ₀ ,t)/dt ² просто как обозначения неизвестных функций, которые зависят от параметра t и r ₀ . Продифференцируем по параметру t первое равенство в (10), уравнение (12) и левое равенство в (11) и вычтем их почленно из (А.1), (А.2) и (А.3) соответственно. Тогда

6 u i = 5 r 2 ,                                        (A.5)

д(5^1-у-2) + х-д(5у1-2) + д(х-у- 5zi) = _р0Ыg д (х0,У0,20) д (х0,У0,20) д (х0-у0-20)        р2 р дr        9

6 г¹ =    ( r ⁰ ,O - д₍ [rt r ⁰ ,*)] ,

^{9 2 г}          8 ^д r

⁶ r 2 = дt 2 ⁽ r ⁰^    дЛдt ⁽ r ⁰ , ^ ^-

⁶ r 1      (Л 1 ^{- b} y 1 ^- ^ z l ),

⁶ r 2 = ^{( b} X 2 ^{- b} y 2 ^{- b} z 2 ⁾,

д р         д

⁶р = S ^-‘l ^- at M -

^b u 1 =

^д u        8

at ( r ⁰ 'i)^- ^ [u ( r ⁰ 'i)]'

где	1 /8f s ( р )    д 2 р 5 ( рЛ		8P s ( р )г _ G = 6 u 2 - р д р	(A.7)
	р2 ^ д р      р	д р 2 ур v р
G = ——	1 д р д( р -у-г) р д‘ д(х 0 -у 0 -г 0 ) 1 д р д(х, р -г)	+ д( 5 р -у,г) + д (х 0 -у 0 -2 0 ) । д( Ь ж 1 - р - г) +	д( р - 5 у 1 -г) + д( р -у- 5 z 1 ) д(х 0 -у 0 -2 0 ) д (х 0 -у 0 -2 0 ) ^(х-бр^г^ + д(х- р - 5 г 1 )
Р 0Л0 )	р д‘ д(х 0 -у 0 -2 0 ) 1 д р д(х-у- р ) _ р д‘ д(х 0 -у 0 -2 0 )	д (х 0 -у 0 -2 0 ) + а(5^,_ р ) + д (х 0 -у 0 -2 0 )	д(х 0 -у 0 -2 0 ) д (х 0 -у 0 -2 0 ) а(х15 у 1 1 р ) + д(х-у- 5 р ) д(х 0 -у 0 -2 0 ) д(х 0 -у 0 -2 0 ) _

⁶ u 1      ^{( b} u _T 1 ^{- b} u _y 1 ^{- b} u _z 1 ^{)-    6} u 2

д2и        д дu д^ (r0-t) — ^     (r0-t)] '   6u2 = (b^-2- Лу 2' A 2).

Продифференцируем правую часть выражения (10) по параметру t и вычтем его из правой части выражения (11). Учитывая (А.1), имеем:

С      ¹ Ле     X^X^ ^{( r}0)     r d3 г"   ¹ J      ‘) X^^ •^ 0 ⁾⁶ r‘lj3 _".

6r2 = — 4П J (6r1 — 6r‘1) X     |r — r"|3 d r0 — 4П J (r — r ) X |r — r"|3     d r0

+ ^ /( r — r " ) X ( ЛЛ _rI⁰⁾ r " ( r — r " ) • ( 6 r 1 — 6 r‘1/) a —

4n J            \    |r — r 1/

‘ ам^(r 0 ^-t)

X г ( 5_{£ 1}-_мм( г 0₂^о ,3_r " _— [ ^{( r — r ) b} д‘

4n J         |r — r"|3           0    4n J        |r — r"|30

+4П/

( r — r " )M ( r 0 -1) | r — r " | ⁵

( r

^{— r} " ) • ⁽⁶ r 1

^{— 6} r ‘ 1 ⁾d 3 ^r 0 ^-

(A.8)

где

5 ЭМ ( r 0 ,t) = Э(Ь _и ._т1у у',2 ’ ) + 8(иД г 0 ,Д, 5 ^ ’ 1 , г ’ ) + д(и _ж ( г 0 ,^,у', 5 _гЧ) +

8t            8 r 0                 д r 0                    д r 0

+ a^^x ’ iaV r crt^^ + ^д (^х, ^у- i ,z ‘ ) + 8(^x ’ ,u^r0^)₁ 5 ‘ i ) + 8 r 0                 д r 0                 д г 0

+ d(bx‘i,y',uz(r',t)) + д(х', 5y‘i,uz(r0,t)) + 8(х,у , 5И^ Д д r0                    д r0                 д r0

д r’         8                      д u

Sr’i = ^t(r0,t) — д^ [r (r0,t)],      5u‘i = у^(r0,t) — at•

Продифференцируем теперь правую часть выражения (11) по параметру t и вычтем его из уравнения (А.4). Находим, что

δ

u2 — у [^{( 5 E} i + Si^c^ rQ , 4 п

(A.9)

5E i — — ( 5 r 2 — S r ‘ 2 ) x

И( г 0 ) • У Г ’ | г — r ’ | 3

(I r дt

I Д дt

x

( _Ш 0 ( г 0 ) •У 0 ) 5 г ‘ 1 + | г — r ’ | 3

+ 3

(I- r дt

I Д дt

x

И( г 0 ) -У 0 ) г ’ | г — r ’ | ⁵

( r

^— r ’ ) • ⁽ 8 r i

^— 5 _Г‘Д ^—

—

(r — r ’) x

ш г ) •У 0 ) 5 г ‘ 2 | г — r ’ | ³

⁽ 5 r i ^— 6 r ' i ) ^x

⁽ ш 0 ^(г 0 ⁾ •^y,,i ¹ r ’

| r — r ’ | ³

( _Ш ' ( г 0 ) • У ' )-_д^ г ’

^{+ 3} ( ^{r —} r ) ^x ------ | r _— r ’ | 5------^{(r —} r ) • ⁽ 5 r i ^— 5 r ‘ i ) ⁺

+ 3( r — r ’ ) x ( < " 0 <^{r 0 )} ;У^{0 ) г} ’ ( г — r ’ ) • ( S r , — S r . 2 )L

| r — r ’ | ⁵

I 5     5       / ^ r^- • У ' ) г ’            / ^{д д} Л\

+ 3(Sri — Sr‘i) x      hr—r’     (r — r )• ^tr — ^tr

_{(          A}    f ( ^ ' ( rG ) • V 0 ) 5 r ‘i,           f 8      8 Д^ ,

+ 3(r — r) x        0          (г — r ) • r — r + v                   |r — r’|5      v          Vdt     8t J J

(Ш'(г0) ^0)^,         x / 88

+ 3(r — r) x                   (6ri — 6r‘i) • ( —r — —r I — у     |г — r’|5                     \дt дt / /

((ш0(го) -У0)г’ (         f 8     8 д\ /\\

• ^— 15( r ^{— r} ) ^x I _|r — r ’ | 7     ^( r ^— r ) • ^5, r ^— !t^г )) (( Г ^{— г} )( 6 r l ^— 6 r ‘ ^{i )}) I

(        ^д2 ^{М (r} 0 ^,t)

— ^(Г — r ^{) 5}     I, ,      _— (⁶ r 2 — ⁶ r ‘ 2 )M( r 0 ,t) +

| r — r ’ | ³                        | r — r ’ | ³

-

+3

( r

-

+ 3

- 6^ )) M ( r 0 ,t)

( S r i

-

+3

+3

^r ' ^)M(r 0 ^,t)

| r

-

r ^′ | ⁵

( r

5 r ‘ i )

| r

-

| r - r ^′ | ⁵

d ² M ( r 0 .t)

at2

f dr   d r' d dt - dH

δ

-

r ^′ | ³

-

| r

-

r

-

r ‘ ) • ( 6 r 1

-

-

dM ( r 0 ,t)

r ^′ | ³

at

^dM ( r o .^

at

+

| r

| r

-

-

r ^′ | ⁵

r ^′ | ⁵

+

δ

^{dM ( r} 0 ^{,t )}

dt

+

d r

⁽ 5 r i ^- 5 r ‘ i ) •

-

d r ’

+3 dt

( r

-

^r ' ^)M(r 0 ^,t)

| r

-

r ^′ | ⁵

( r

-

⁽ 5 r i ^- 5 r ‘ i ^)M( r^ )           / ^d r ^d r \

⁺³      k-r p 5      ^{(r - r}) • I dt ^- at Г

( r - r ' )M (Г_п , t)             d r d r ’

^{- 15}     | r - rr   ⁽r ^{- r}> • (a ^- at)^{( r - r} ' ’ • ⁽⁶r i ^- ^

• ^{6 d} ^r'’ ^ = Д (⁶ « i 2 .y ' .^z ' ) ⁺ Д ⁽ “ r ⁽ r o . М. ⁸ ( ' 2 ,^z ' ) ⁺ Д W^r o >M ⁵ « - 2 ) ⁺ + JL (^^ + A f .y. U + A L‘ _A^. U + d r 0 у dt             )    d r 0 \ dt              I    d r 0 \     0 dt /

d Л    dy' ‘ d          ‘ dz‘      d        ‘ , cdz'

⁺ d r^" (^{6 ж} ‘ ² . “ ^ ( r o .^t). ^Z ^ ⁺ dr^" ( ^ . ⁶ “ ^ 2 . ^Z ) ⁺ dr^" ( ^ . “ ^ ( r o .^t). ⁶ “ ^ 2 ^ ⁺

+ fd|‘. 641. z'^ + A f.'. d-“^. 6,i^ +    f d-l,Uy(r‘. t). SJ+ dr0 \ dt    y I dr0 \ dt I    dr0 \ dt/

+ f6i4.    у ,'d + a f.,5„‘„d4) + d \S_U((r6.t) d dr0 \          dt I    dr0 \ y dt I    dr0 \

+ dr^ (6ж‘2.y . “z(ro.t)^ + dr^ (Ж . 6(‘2. “z(ro.t)^ + dr^ (Ж .y . 6“^2^ + d (dx'        , ‘ Л d  ( ‘ dy’     \ d  (dx’ ‘\

⁺ d ro ( dt . ^{б (}‘¹ . “ ^{z (r o} . ^t)) ⁺ d ro ( ^x ’ dt ’ ^{5 tizi}) ⁺ d ro ( dt ’^y . ⁶ “ ^zi) ⁺

, ^d (c     ^dy'      ( '         , ^d f ' .      ^d“ , ^(r o .^t) d , ^d (я I ^d“, ^(r o .^t) d

+ dro (6 ■ dt1 “(ro.^ + dro (х.б(‘1.    dt J+ dro (6 ■y. dt У a2r‘, ‘        д ar, ‘

5 r ‘ 2      dt 2 ⁽ r ^{o ,t)}    dt dt ⁽ r ^{o ,t )}

5 u ‘ 2 = ^ ( r 0 ,^t)

—

^д P¹'¹ ‘ .x at at ⁽ 0 , )

Пусть на некоторой поверхности S в пространстве R 3 известны величины r ( r _o ,t) , p ( r o ,t) , u ( r o ,t) , д u ( r o ,t)/dt , д r ( r o ,t)/dt , д p ( r o ,t)/dt , д ² u ( r o ,t)/dt ² , д ² r ( r o ,t)/dt ² , которые согласуются следующим образом:

д r        д д r dt(ro,t) - at dt (r0’t)j=0’

t r ^(r o ^{,t) -} It [ t r (^ l =^{0 r} o ^{E S,t E [0,T}]’ дt ²          dt dt

(A.10)

du at(ro,t)

-

_д dt

" du, at ■'   = 0,

д 2u        a at2 (o,t) at

" ^au, at ^{(r o ,t)}

= 0,

r o E S,t E [0,T ], (A.11)

др        д dt(ro,t) - dt [p(ro,t)]=0, ro E S,t E [0,T].                (A. 12)

Пусть мы имеем решение системы уравнений (10)–(12), (А.1)–(А.4) от неизвестных функций r ( r o ,t) , p ( r o ,t) , u ( r o ,t) , д u ( r o ,t)/dt , d r ( r o ,t)/dt , д p ( r o ,t)/dt , д ² u ( r o ,t)/dt ² , д ² r ( r ₀ ,t)/dt ² , которые заданы на поверхности S и согласуются сообразно условиям (А.10)–(А.12). Пусть на этом решении линейная система (А.5)–(А.9) из 13 интегро-дифференциальных уравнений и 13 неизвестных δ r 1 , δ r 2 , δ ρ с условием на поверхности S

5 r i = 0, 5 r 2 = 0, 5 u i = 0, 5 r 2 = 0, 5 р = 0, r o E S, t E [0, T] (A. 13)

имеет только нулевое решение в пространстве R3 . Тогда согласно самому способу получения системы уравнений (А.5)-(А.9) для решения r(ro,t), p(ro,t), u(ro,t), дu(ro,t)/dt, дr(ro,t)/dt, дp(ro,t)/dt, д2u(ro, t)/dt2, d2r(ro, t)/dt2 выполняются соотношения (А.10)-(А.12), но во всем пространстве R3. Кроме того, из левого равенства уравнения (11) и первого равенства в уравнении (10), следует, что dPs (p)

-

VP   au,   .,   a

V = at (w) = at [u

д r at(ro,i)

дд at at [r(ro,t)l .

(A.14)

Система уравнений (А.14) с учетом уравнений (12)–(15) является системой уравнений Эйлера в переменных Лагранжа. Скорость и плотность тогда будут определяться по формулам u = дr/dt(r_o(r, t), t), p = p(r_o(r, t), t).

Следует отметить, что r(r_o, t), p(r_o, t), u(r_o, t), du(r_o, t)/dt, dr(r_o, t)/dt, dp(r_o, t)/dt, д²u(r_o, t)/dt², д²r(r_o,t)/dt²не могут быть заданы на поверхности произвольно. Они фиксируются заранее из начального распределения r(r_o,t) = r_o, dr(r_o, t)/dt|_t=_o= = u_o(r_o) во всем пространстве R³. Эти данные могут быть найдены, например, из независимых экспериментальных измерений.