Эффект гидры в модели динамики численности эксплуатируемой популяции, структурированной по возрасту и полу

В настоящей работе продолжен анализ влияния избирательного промысла на динамику численности структурированной популяции [1]. Предполагается, что рождаемость зависит от соотношения численностей полов и количества формируемых пар. Регуляция численности осуществляется путем лимитирования выживаемости молоди, когда с ростом численностей половозрастных классов наблюдается уменьшение выживаемости неполовозрелых особей. С учетом промысла, осуществляющегося после периода размножения, система имеет вид:

' P n + 1 = a min f n ,2 f_nm_n / ( f n / h + m n ) )(1 - u p )

< f n + 1 = R¹ - P n - Pffn ⁺ m n )) P n ⁺ s f n ⁾⁽¹ - u f )       , (1)

, m n + 1 = ^{( (1} - ⁸ ) ⁽¹ - P n - Pf fn ⁺ m n ) ) P n ⁺ v m n ) ⁽¹ - u m )

где n – номер сезона размножения; p , f и m – относительные численности неполовозрелых особей, половозрелых самок и самцов соответственно; a – коэффициент рождаемости (среднее число

потомков, приходящихся на одну брачную пару); δ – доля самок среди новорожденных; s и v – выживаемости половозрелых самок и самцов соответственно; ρ характеризует относительный вклад половозрелых особей в плотностно-зависимое лимитирование выживаемости молоди; h соответствует среднему размеру гарема и характеризует тип брачных отношений в популяции; u_p , u_f и u_m – доли изъятия молоди, взрослых самок и самцов соответственно.

Рассматриваются частные случаи модели (1), когда изъятие особей осуществляется либо из младшего возрастного класса ( u_p ; u_f = u_m = 0), либо из группы половозрелых самцов ( u_m ; u_p = u_f = 0) или половозрелых самок ( u_f ; u_p = u_m = 0). Проведено исследование структуры популяции в равновесном состоянии и определены условия ее устойчивости, для каждого случая модели (1) решена задача оптимизации равновесного промысла.

Проведенное исследование показало, что избирательный равновесный промысел из половозрастных групп может демонстрировать эффект гидры. Под эффектом гидры понимается увеличение равновесной численности эксплуатируемой группы популяции с ростом доли ее изъятия. Поскольку в данной работе рассматривается промысел после размножения и вычисляемая равновесная численность популяции по модели (1) есть количество особей после промысла, то эффект гидры является скрытым [2]. Для его выявления отдельно анализируются изменения численностей эксплуатируемых классов после промысла (p, f, m) и после размножения, но до промысла ( p~ , ~f , m~ ), которые связаны соотношением: p = ~(1 - up), f = f (1 - Uf), m = m(1 - um). Именно рассмотрение численности после размножения и до промысла позволяет обнаружить данный эффект. Отметим, что границы области устойчивости равновесных численностей эксплуатируемой группы до и после промысла совпадают, т.е. их качественная динамика одинакова. Область существования эффекта гидры рассматривается только в области устойчивости стационарных решений. Заметим, что равновесные численности неэксплуатируемых групп до и после изъятия не отличаются.

В качестве примера проиллюстрируем эффект гидры для случая промысла неполовозрелых особей с постоянной долей изъятия u_p (рис. 1). На рис. 1 видно, что если оценка популяционных параметров располагается в области существования эффекта гидры (рис. 1а), то введение изъятия или увеличение его интенсивности может привести к росту численности изымаемой группы вида (рис. 1б, в). Так, с ростом интенсивности изъятия

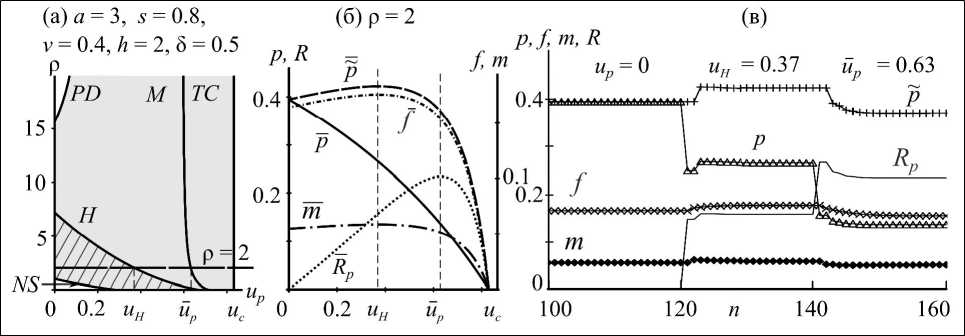
Рис. 1. Области устойчивости (выделена заливкой) неподвижных точек системы (1) и существования эффекта гидры (штриховкой) на плоскости параметров ( u_p , ρ) (а). Изменение численностей неполовозрелых особей после размножения и до промысла ^~ p и после промысла p , зрелых самок f и самцов m и количества изъятых особей R_p в равновесном режиме (переменные с верхним подчеркиванием) от доли изъятия молоди u_p (б) и во времени n при разных u_p (в). TC , NS, PD – линии бифуркаций транскритической, Неймарка-Сакера и удвоения периода соответственно, H – линия максимальных значений ^~ p , M – линия оптимальных значений изъятия

Fig 1. Stability domains (highlighted in gray) of the system fixed points (1) and the hydra effect (shaded area) existence on the parameter plane (up, ρ) (a). Changes in the number of immature individuals after reproduction – before harvest ~p and after harvest p. Changes in the number of mature females f and males m, and the number of harvested individuals Rp in the equilibrium (variables with an upper underline) from a younger age class harvest proportion (b) andover time n at different up (c). TC, NS, PD are the transcritical and Neimark–Sacker lines, and doubling of the bifurcations period, respectively; H is the line of maximum values ~p , M is the line of optimal values of harvest молоди up до значения uH допромысловая равновесная численность p~ увеличивается до некоторого уровня, в то время как послепромысловая численность молоди p снижается (рис. 1б). Повышение численности неполовозрелых особей после размножения при увеличении доли их изъятия (до уровня uH) также прослеживается при рассмотрении траекторий системы (1) от времени (рис. 1в). Отметим, что в случае изъятия молоди увеличение их численности после размножения, но до промысла, наблюдается наряду с ростом равновесной численности зрелых самок и самцов.

Дальнейшее увеличение изъятия u_p смещает оценку популяционных параметров к линии максимальных значений допромысловой численности H (рис. 1а), при пересечении которой численности всех половозрастных групп снижаются (рис. 1б, в). Промысел с оптимальной долей изъятия u_p = u _p обеспечивает добычу наибольшего количества особей, вместе с тем при его осуществлении численности половозрастных классов популяции уменьшаются (рис. 1б, в).

Таким образом, реализация дифференцированного промысла, вследствие которого возникает эффект гидры, приводит одновременно к увеличению численности оставшейся части популяции

(с учетом прироста после размножения) и росту количества добытых особей. При этом равновесный промысел с оптимальной долей изъятия хотя и обеспечивает добычу максимально возможного количества особей, однако приводит к снижению численности популяции.

Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН.