Эффект спонтанного нарушения симметрии в моделях типа II, IV по Бьянки

Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным нарушением определенных видов симметрий. "Симметричное обозначает нечто, обладающее хорошим соотношением пропорций, а симметрия – тот вид согласованности отдельных частей, который объединяет их в целое. Красота тесно связана с симметрией", – писал Г. Вейль в своей книге "Этюды о симметрии". Он ссылается при этом не только на пространственные соотношения, т.е. геометрическую симметрию. Разновидностью симметрии он считает гармонию в музыке, указывающую на акустические приложения симметрии.

В широком смысле симметрия – это понятие, отображающее существующий в объективной действительности порядок, определенное равновесное состояние, относительную устойчивость, пропорциональность и соразмерность между частями целого.

Важным понятием в современной физике является понятие калибровочной симметрии. Калибровочные симметрии связаны с инвариантностью относительно масштабных преобразований. Так, в СТО физические законы не из-

меняются относительно переноса (сдвига) системы координат. Траектории движения остаются прямолинейными, пространственный сдвиг остается одинаковым у всех точек пространства. Таким образом, здесь работают глобальные калибровочные преобразования.

Одной из важнейших особенностей геометрических симметрий является их связь с законами сохранения. Значение законов сохранения (законы сохранения импульса, энергии, заряда и др.) для науки трудно переоценить. Дело в том, что понятие симметрии применимо к любому объекту, в том числе и к физическому закону.

Наиболее общий подход к взаимосвязи симметрий и законов сохранения содержится в знаменитой теореме Э. Нетер. В 1918 г., работая в составе группы по проблемам теории относительности, она доказала теорему, упрощенная формулировка которой гласит: если свойства системы не меняются относительно какого-либо преобразования переменных, то этому соответствует некоторый закон сохранения.

Взаимосвязь симметрии и асимметрии рассматривается современной наукой в различных аспектах, охватывающих саморазвитие материи на всех ее структурных уровнях.

Так, современное видение эволюции Вселенной основано на идее о т.н. спонтанном нарушении симметрии исходного вакуума. Под исходным вакуумом понимают состо- яние материи до Большого взрыва, когда вся материя была представлена физическим вакуумом.

В настоящее время считается, что истинный физический вакуум - это состояние материи с наименьшей энергией. Идея спонтанного нарушения симметрии исходного вакуума означает отход от общепринятого представления о вакууме как о состоянии, в котором значение энергии всех физических полей равно нулю. Здесь признается возможность существования состояний с наименьшей энергией при отличном от нуля значении некоторых физических полей и возникает представление о существовании вакуумных конденсатов - состояний с отличным от нуля средним значением энергии. Спонтанное нарушение симметрии означает, что при определенных макроусловиях фундаментальные симметрии оказываются в состоянии неустойчивости, а платой за устойчивое состояние является асимметричность вакуума. (Для такого вакуума введен термин "ложный вакуум")

Один из наиболее вероятных сценариев эволюции Вселенной включает инфляционную стадию (раздувание) от "ложного вакуума" - вакуума, обладающего огромной энергией. Такой вакуум обладает стремлением к гравитационному отталкиванию, обеспечивающему его расширение.

"Ложный" вакуум представляет собой симметричное, но энергетически невыгодное, а следовательно, нестабильное состояние. В свете инфляционной теории эволюция Вселенной предстает как синергетический самоорганизующийся процесс. Если считать Вселенную замкнутой системой, то процессы самоорганизации могут быть рассмотрены как взаимодействие двух открытых подсистем -физического вакуума и всевозможных микрочастиц и квантов полей. Согласно этой теории в процессе расширения из "суперсимметричного" состояния Вселенная разогрелась до температуры, соответствующей Большому взрыву. Дальнейшее ее развитие по мере падения температуры пролегало через критические точки бифуркации (ветвления), в которых происходили спонтанные нарушения симметрий исходного вакуума. Схематично этот процесс представляется в следующем упрощенном виде:

1-я бифуркация: нарушение симметрии (тождества) между бозонами и фермионами привело к разделению материи на вещество и поле;

2-я бифуркация: нарушение тождества между кварками и лептонами; симметрия Вселенной нарушается до симметрии, отвечающей сильным взаимодействиям и симметрии, отвечающей электрослабым взаимодействиям; нарушается также симметрия между веществом и антивеществом: частиц вещества рождается больше, и вся наша Вселенная оказывается построенной из вещества;

3-я бифуркация: спонтанное нарушение симметрии электрослабого взаимодействия, что обнаруживается нами в виде различия между электромагнитным и слабым взаимодействием.

4-я бифуркация: возникают протоны и нейтроны.

Дальнейшая эволюция Вселенной приводит к возникновению водорода, гелия, ионизованного газа, звезд, галактик и т.д.

Спонтанное нарушение симметрии вакуума выражается в том, что он отдает энергию на рождение микрообъектов, на приобретение их масс и зарядов, вследствие чего плотность энергии вакуума уменьшается.

В [1] рассмотрено несколько примеров спонтанного нарушения симметрии скалярного поля с самодействием во внешних полях. К спонтанному нарушению симметрии приводит, в частности, взаимодействие с сильным статическим либо высокочастотным переменным электрическими полями. В [1] показано, что гравитационное поле, описываемое метрикой однородного изотропного пространства открытого типа, также служит инициатором спонтанного нарушения симметрии в первоначально симметричной системе. Этот эффект представляет интерес, во-первых, потому, что дает механизм возникновения ненулевых масс элементарных частиц, обусловленных кривизной пространства-времени, т.е. в конечном счете наличием материи во Вселенной.

Во-вторых, эффект спонтанного нарушения симметрии в искривленном пространстве-времени позволяет связать единые калибровочные теории слабых, электромагнитных и сильных взаимодействий с возможным изменением геометрии на малых расстояниях. В большинстве случаев спонтанное нарушение симметрии из этих теорий вводится искусственно, путем приписывания отрицательного квадрата массы хиггсовской частице.

Для безмассового поля вакуумное состояние со спонтанно нарушенной калибровочной симметрией обладает отрицательной энергией и является предпочтительным (по сравнению с обладающим нулевой энергией симметричным состоянием) на всех стадиях эволюции.

Исследование эффекта спонтанного нарушения симметрии в метриках типа II и IV по Бьянки

Спонтанное нарушение калибровочной симметрии в космологии, в том числе в космологических моделях с вращением, исследовалось в работах [2, 3]. Мы рассмотрели эффект спонтанного нарушения калибровочной симметрии в космологических моделях с расширением и вращением с метриками типа II, IV по Бьянки.

Рассмотрим модели с метрикой Бьянки:

ds ² = dt ² - 2 R ( t) n dx i dt - R ² ( t ) Y dxdx^J ,

П = Mae?, Yj = ^beieb, где

M a , A _ab - const ( a, b = 1,2,3) (det X _ab * 0) .

Возьмем коэффициенты в виде ма = {0, M, 0} и ЛаЬ = 0  Л0

<0   01

Работа проведена для метрик Бьянки

	" 1	- z	0
типа II:      eaa =	0	1	0
	1 0	0	1 7
	r 1	0	0	^
и типа IV: e " =	0	ex	0
	< 0	xex	ex	7

При рассмотрении сопутствующей жидкости в таких пространствах расширение л  3 R (t)

и =-----, сдвиг СУ = 0 .

R ( t )

Рассмотрим эффект спонтанного нарушения калибровочной симметрии для метрики типа II по Бьянки:

Параметры модели:

вращение      ш = ----,

2 R ( t )

R ( t ) m ускорение a =-----.       .

R ( t ) ^A + m ²

При этом мы предполагаем, что одним из источников гравитационного поля является сопутствующая идеальная жидкость, у кото-

M рой вращение ш = .

Рассмотрим самодействующее комплексное скалярное поле р(t) в искривленном пространстве с метрикой (1), удовлетворяющее уравнению giУХ№+Mр -1 R-р+Л рр2 = 0,

( Л> 0)

которое получается из плотности лагранжиана

L = T- g [ g i д рд к р - M рр +

. R       лл . ч21

+-рр--(рр)], 66

инвариантной относительно калибровочных преобразований вида р ^ рехр(ia), р ^ р exp(-ia).

Обозначим |0> гейзенберговское вакуумное состояние, определенное при t=t pl . Из пространственной однородности (1) вытекает, что если вакуумное среднее р отлично от нуля, то оно может зависеть только от t :

< 01 р ( t , x , y , z ) 10 >=< 01 р ( t ) 10 >= q ( t ) . (4)

Вследствие С-инвариантности состояния |0> величина q – вещественна. Отличие q от нуля означает спонтанное нарушение калибровочной симметрии. При этом в ходе усреднения (2) по состоянию |0> предполагается

< 01 р р ²1 0 >-< 01 р * |0 ><  0| р |0 >  ² =

3                                                  (5)

= q •

Для метрики (1):

g = - R⁶ ( a + m ) , A + m >  0;

ds ² = dt ² + 2 ^ R ( t ) [ zdxdt - dydt ] - R ²( t )* *[ ( A z ² + 1 ) dx ² - 2 A zdxdy + A dy ² + dz ² ]

R = —

2 ( 12 RR + 12 R ² - A - ; ²)

2 R ² ( Л + ^ ²)

,( R = R ( t )),

M ² + ¹ R o ⁰ — ¹ R 1 g ² +^Л g ⁴.     (9)

3     6 J      6

„о        з R a

R 0     R ( A + ; ²)^.

Исследуем эффект спонтанного нарушения симметрии скалярного поля ф в простран стве-времени с метрикой (1) в двух случаях:

1) для R(t)=const , усредненное уравнение (2) для метрики (1) примет вид q — ag + fig3 = 0,           (6)

где dq q = Of ’ “ =

( A + ; ²)( A — 12 M ² R ²) 12 R² A

Подставляем решения уравнения (6) в (9), находим

E(q 2;3 ) =

E(q 1 ) = 0,

( A — 12 M ² R ²)²_л

< 0 .

96 R ⁴ Л

Рассмотрим космологическую модель, где R и M – постоянные, при этом за счет ва- рьирования параметров источников гравитационного поля можно менять A и ;, тогда эффект спонтанного нарушения симметрии будет при любых A ^ 12M2R2 и он не зависит от скорости вращения модели, определяемой вращением идеальной жидкости

^{( A} + ^{;2 ) л}

^P     3 A

^ = —

2 R

При этом можно считать q=const , ввиду того, что R ( t )= const .

Тогда уравнение (6) имеет два ненуле-

Таким образом, энергетически более выгодным будет несимметричное вакуумное состояние | 0> ( q * 0), что означает спонтан-

вых решения:

g 2,3 = ±

' A — 12 M² R ² У2

I    4 ^{R 2 Л}   J

A — 12 M ² R ² >  0

ное нарушение симметрии вакуума.

2) для R ( t )= vt , M =0, уравнение (2), усредненное по гейзенберговскому вакуумному состоянию с учетом древесного приближения, имеет вид

и q 1 = 0. (7)

Предпочтительность выбора решений q 2,3 ^ 0 из соображений минимума энергии дает возможность выявить спонтанное нарушение калибровочной симметрии. В этом случае несимметричное вакуумное состояние |0> энергетически более выгодно, чем симметричный вакуум. Используем метрический тензор энергии – импульса для скалярного поля ф :

3 ^{g +} -^{д —}

A + ; 6 A

R > 7+ dr ² Л g ’ = 0 , (11) t        3^ A

где

~ A ( 12 v ² — A — ; ² )

R 0 =—   \ 2₍^ 2   .     (12)

2 v ( A + ; )

Сделав замену g =

f ( t ) t

, получим

T = v ф v v +v ^v ^ v ф

—

у 2 У (A + Г ft2 + ft--—

I 6 A

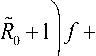
A + ; 3 A

Л f ³ = 0, (13)

—^ [v V v ^ — m V v ]

—

сделаем замену т = In t , получим

—

—

■ R^v + ¹ s ^v R + v ^v v ^{;      ;}

А

—

*

г □ vv +

f"

' A + ;² .    6 A

R + 1 1 f + ^A + r 2 л f ³ = 0, J        3 A

+^Л г ; (••.

где                 ^f ' = d- ,             ⁽¹⁴⁾

а т

где R ; - тензор Риччи, S ^ - единичный тензор.

Вакуумная плотность энергии для данной модели равна

E=<0 | Too I 0>= а уравнение Дюффинга (14) имеет два устой- чивых решения и одно неустойчивое:

A = 0, f >3 =± ^A • -^ A >  0, Л> 0. (15)

V Л 2 v

В качестве начальных условий (14) возьмем:

■ f ⁽ t pi ) = ± 2 2 ? • f ’( ’ ") = 0.

Уравнение (14) имеет ненулевое решение, соответствующее перестройке вакуума в состояние с нарушенной калибровочной симметрией.

Тогда решения уравнения (11):

^ 1

q x = 0, q 2,3 = ±\-'ti .       ⁽¹⁶⁾

V Л 2 vt

g = -e^{4 x}R ⁶ ( 2 + p ) , 2 + p >  0, „    2 ( 12 RR + 12 R ² - 2 - p - 12 ) - 11 p²

R =               2 R ² ( 2 + p ²)            ,

( R = R ( t )), R 0 = P ² - 3 ^RR 2 .    (19)

R ² ( 2 + p )

1) Для R ( t )= const можно считать q=const и усредненное уравнение (2) для метрики (18) примет вид

- a q + eq³ = 0 ,        (20)

Обсудим теперь вопрос о предпочтительности вакуумного состояния |0> с энерге-

где

тической точки зрения. Подставим (16) в выражение (9) и, учитывая также, что R ( t )= vt ,

a =

2 ² + 2p ² + 12 2 + 11 p ² -12 M ² R ² ( 2 + p ²)

M =0, получим:

E(q 1 ) = 0,

2 ² (48 v ² - 2 - p ²)

E(q 2;3 ) =                        .

96 1 ⁴ v 4 ( 2 + p ) Л

12 R 2

(2 + p2 )л в = 4-----f—, a > 0, в > 0.

,

При      выполнении      условия v2 < (2 + p2 ) /48 вакуумная плотность энер-

Решения уравнения (20) q₁ = 0 и q _{2 3} ^ 0 .

Ненулевые решения уравнения (20):

гии E(q 2;3 ) отрицательна, что эквивалентно следующему неравенству: ш ² > 12 a ² (где a -ускорение, ш- вращение модели).

Таким образом, так же, как и в предыдущем случае, энергетически более выгодным будет несимметричное вакуумное состояние |0>, и ненулевые решения (16) уравнения (11) соответствуют перестройке вакуума в состояние с нарушенной калибровочной симметрией.

Рассмотрим эффект спонтанного нарушения калибровочной симметрии для метрики типа IV по Бьянки:

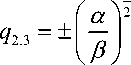
1   (21)

" 2 ² + 2p ² + 12 2 + 11 p² _ 3 M 2 ) ²

4 R ² ( 2 + p ²)Л      Л

При усреднении тензора энергии-импульса (8) по состоянию |0> вакуумная плотность энергии Е для метрики (18) будет аналогична (9).

Для R ( t )= const имеем:

ds2 = dt2 - 2pR(t) [exdydt + xexdzdt ] -- R 2( t)[ dx2 + 2e2 xdy2 +

+ 2 2 xe² x dydz + ( 2 x ² + 1 ) e^{2 x}dz ²].

Аналогично предыдущему параметры модели: 3R(t) расширение    d = ppj 2 + p +1 вращение ш = —^=

2^ 2 + p² R ( t )

R (t )p ускорение a =-----..

R ( t ) J 2 + p²

Для метрики (18):

2 M ²

^{E ( q} 2,3 ) = ^{q (} ₂

_ 3 p ² + 2 ² + 2p ² + 12 2 ■

24 R ² ( 2 + p ²)   )

Требуя выполнения условия E ( q _{2 3}) <  0, по-

лучаем условие для нарушения симметрии:

M ₂R 2 <  3 p 2 ⁺ 2 ⁺ ^ ⁺ ,₂ , ,   (23)

12 ( 2 + p ²)

что эквивалентно следующему неравенству:

M2 <

3 p ² + 2 ² + 2p ² + 12 2 3 p ²( 2 + p ² + 1)

или, если исключить параметр 2 :

M2 R2 <---и——+2 и2

12(4a2 R2 — и)  3

— 3 a² R ² + 1.

—

v

<     4v 2 a2 — a2

16(4v2 a2 — (и2 +1) a2

2) Рассмотрим случай R ( t )= vt , M =0.

Уравнение (2) с учетом (5) для метрики (18) будет иметь вид (11), где

v ² a²

12 a ²

⁺ 6,

Л (12 v2 — Л — и2 —12 ) — 11и2

2 v2 ( Л + и2)

.  (26)

Для получения его ненулевого решения подставим в (14) выражение (26) и получим одно неустойчивое решение уравнения

Дюффинга f = 0 и два устойчивых решения

f 2,3 =±

Л2 + Ли2 + 12Л + 11и2 4 v2 (Л + и2 )Л

Л > 0, Л> 0.

,

Тогда ненулевые решения уравнения (11) будут q 2,³ = f =

где a - ускорение, a — вращение модели.

Заключение

Нами были построены две математические модели эффекта спонтанного нарушения симметрии вакуума для метрик типа II и IV по Бьянки. Найдены условия, при которых происходит нарушение калибровочной симметрии в данных математических моделях.

Результаты данной статьи можно использовать при построении новых космологических моделей с вращением, а также для исследования феномена Хиггса в космологии с вращением .

= ±

Л2 + Ли2 + 12Л + 11и2 ( л+и2 )л

•

1 2 vt ^.

Подставим q = f /t в выражение (9) и, учитывая также, что R ( t )= vt , M =0, получим:

_F(a ь fL 48 v²Л — 3и

E ⁽ q 2,3 ) = 4

'2 — Л2 — Ли2 — 12Л

24 v2 (Л + и2)

. (29)

Нарушение симметрии будет при ( E ( q ) <0):

2 J^2 + Л2 + Ли2 + 12Л

48Л что эквивалентно неравенству:

2  3и2 + Л2 + Ли2 + 12Лa <   12Л(Л + и2 +1)

или, после исключения Л :

,

• a2