Эффективность генерации второй гармоники в одномерном фотонном кристалле из изотропного материала

В настоящее время большой интерес вызывают работы по генерации второй гармоники в изотропных средах. Традиционно используемые для удвоения частоты оптического излучения нелинейные материалы достаточно дороги и сложны в обработке, хотя и позволяют преобразовывать излучение во вторую гармонику с эффективностью порядка 50–60 %, тогда как изотропные среды позволяют создавать структуры и объекты практически любой сложности форм и структуры. Актуальность этой темы обусловлена возможностью изготовления периодических структур из подобных изотропных сред, например, для ГВГ в одномерном фотонном кристалле. ГВГ в одномерном фотонном кристалле достаточно хорошо изучена, но лишь для нелинейных сред. Так, в 2003 году была получена ГВГ в одномерном фотонном кристалле с эффективностью преобразования излучения во вторую гармонику около 1 % [1]. Кроме того, была рассчитана эффективность преобразования излучения во вторую гармонику для нелинейного фотонного кристалла. Эффективность преобразования составила 10 ^–2 –10 ^–3 [2].

ГВГ в изотропных средах затруднена из-за отсутствия в таких средах нелинейности второго порядка или χ(2), а также из-за трудности выполнения условия фазового синхронизма, которое в случае одномерного фотонного кристалла выполняется автоматически. Однако в изотропных телах возможна эффективная ГВГ оптического излучения. Впервые ГВГ в изотропной среде наблюдалась в 1981 году, когда случайно обнаружилась ГВГ излучения неодимового лазера в гер-мано-силикатном волокне [3, 4]. При этом эффективность преобразования была невелика и составила около 10 ^–8 . Далее, в 1987 году был предложен механизм, объясняющий возникновение квадратичной нелинейности в изотропных средах [5]. Далее, в 1987 году [6] была предложена теория, согласно которой в волокне при распространении излучения первой и второй гармоник происходит упорядоченная переориентация дефектов, имеющих χ⁽²⁾ ≠ 0, что впоследствии вызывает ГВГ при облучении только первой гармоникой. Для проверки этой гипотезы был проведен эксперимент с оптическим волокном, в котором была достигнута эффективность преобразования излучения во вторую гармонику 0,03 %.

Запись х(2) решетки в одномерном фотонном кристалле

Краткие сообщени^

Согласно работе [5], нелинейность второго порядка может появиться в изотропной среде в случае воздействия на нее полем с неравным нулю средним кубом поля, ³> ^ 0. Если подвергнуть изотропную среду одновременно излучению первой и второй гармоники, то суммарное поле как раз будет имеет неравный нулю средний куб поля и в такой среде будет записана х⁽²⁾решетка:

X ^{2 )}( R ) = а Е 2 _Ю ( R ) e ; ( R ) e ; ( R ) , (1)

где коэффициент а , определяется экспериментально и много меньше единицы.

Был сделан расчет записи такой решетки в одномерном фотонном кристалле с помощью про

граммного пакета MEEP [7]. Была задана структура одномерного фотонного кристалла «стекло-воздух» с показателем преломления стекла 1,5. Размер воздушных и стеклянных промежутков соответствовал и для излучения с длиной волны 1,064 мкм (рис. 1). На рис. 1 светлые промежутки соответствуют стеклу с показателем преломления 1,5, черные - воздуху.

Для наведения нелинейного коэффициента второго

Рис. 1. О^номерный фотонный кристалл стекло-воз^ух

порядка в указанную структуру запускалось излучение двух длин волн - первой и второй гармоники. Пример распространения излучения для разных длин волн представлен на рис. 2.

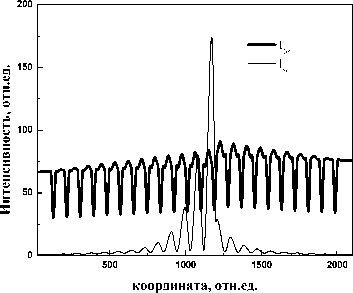
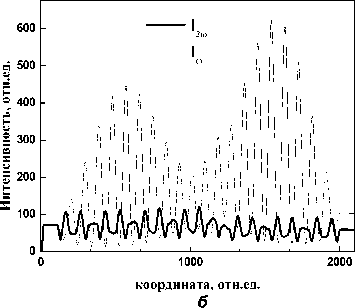
Рис. 2. Распространение излучени^ первой и второй гармоники в о^номерном фотонном кристалле, ^лина волны источника: а ) 1,060 мкм и 0,530 мкм б ) 1,266 мкм и 0,633 мкм

Из рис. 2 хорошо видно, как происходит в фотонном кристалле распространение излучения с длинами волн, отличающимися в два раза.

Таким образом, в данной структуре записывается решетка нелинейности второго порядка (1) с коэффициентом а = 0,01 (рис. 3).

На этом рисунке видно, что х⁽²⁾ решетка формируется неравномерно по всей протяженности фотонного кристалла и равна нулю в воздушных промежутках, так как там возникновение х⁽²⁾ при больших мощностях входного излучения возможно, но кратковременно и носит флуктуационный характер.

Генерация второй гармоники в одномер-

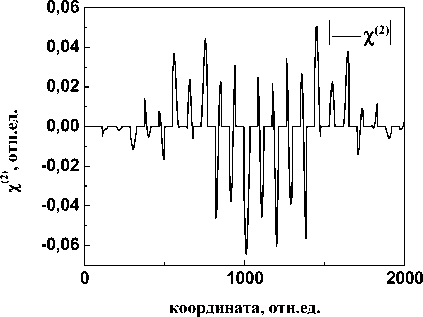
Рис. 3. х⁽²⁾ решетка в одномерном фотонном кристалле при записи ^линами волн 1,226 мкм и 0,613 мкм

ном фотонном кристалле

После того, как в фотонном кристалле сформирована х⁽²⁾ решетка, в данную структуру запускается излучение первой гармоники единичной интенсивности и на выходе из структуры имеет место ГВГ, эффективность которой можно оценить по величине пика, соответствующего второй

Герасимов A.M., Кундикова Н.Д., Микляев Ю.В., Пихуля Д.Г., Терпугов М.В.

Эффективность генерации второй гармоники в одномерном фотонном кристалле ...

гармонике. На рис. 4, а–г показана картина такой генерации для различных длин волн, указанных

на графиках.

10-

-11

-1

-4

-5

-6

-9

-10

10-

-2

-3

-7

-8

0,1

0,2

0,3

0,0

б)

Частота излучения, отн.ед. a )

в )

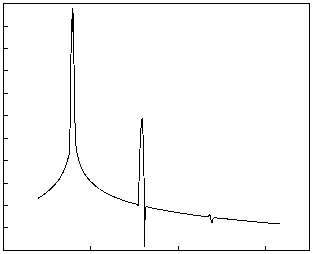
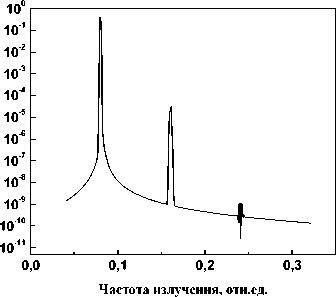
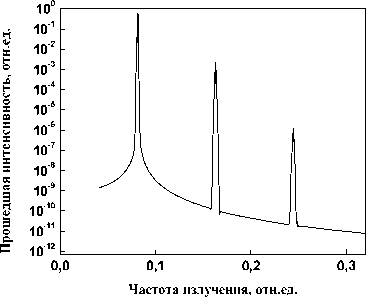
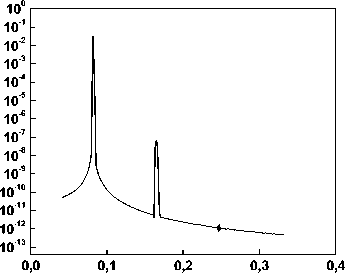
Рис. 4. ГВГ в одномерном фотонном кристалле при длине волны: а ) 1266 нм, б) 1246 нм, в ) 1226 нм г ) 1206 нм

Частота излучения, отн.ед.

г )

Как видно из рис. 4, эффективность ГВГ получается различной при различных длинах волн падающего излучения первой гармоники. При длине волны излучения первой гармоники 1,226 мкм мы видим генерацию не только второй, но и третьей гармоники, которая возникла из-за суммирования частот первой и второй гармоники. В этом случае эффективность ГВГ составила 0,2 %.

Таким образом, проведено моделирование процесса записи χ(2) решеток в одномерном фотонном кристалле с последующей ГВГ при облучении излучением с различными длинами волн. Получена ГВГ для длины волны 1,226 мкм с эффективностью преобразования 0,2 %.