Эффективные сети в модели двустороннего потока с гетерогенностью игроков и малым затуханием

DOI:

An expanding literature in economics and the broader social sciences has documented the significant influence of networks on a wide array of socio-economic outcomes—including labor market dynamics, disease transmission, educational achievement, and criminal behavior. These findings have generated a surge of interest not only in the downstream effects of network structures but also in the underlying strategic processes that determine how such networks are formed and how they evolve over time. At the heart of this literature lies a central concern: the inherent tension between two desirable yet often conflicting properties of networks— namely, efficiency and stability .1 While a substantial portion of the existing network formation literature has focused on characterizing individually stable networks—particularly strict Nash networks— comparatively less attention has been devoted to the structural properties of networks that are socially optimal or efficient . Even rarer are studies that explore the precise conditions under which efficiency and strict Nash equilibrium might be jointly achievable within the same network configuration [1]. This paper contributes to that understudied area by providing a detailed characterization of efficient network architectures in environments that feature player heterogeneity , a well-motivated and widely studied form of agent asymmetry .2

The contributions of this paper are twofold. First, it establishes that under a general class of payoff functions satisfying mild regularity conditions, efficient networks share striking architectural similarities with those that arise in strict Nash equilibria. This result challenges the prevailing intuition that views efficiency and equilibrium as fundamentally incompatible objectives and instead suggests a deeper, previously underappreciated alignment between the two. Second, the analysis uncovers a central design tradeoff that shapes efficient network formation: on one hand, reducing a network’s diameter minimizes the decay of information as it travels across links, thereby preserving its value; on the other hand, smaller diameters tend to require denser connectivity, which imposes higher overall costs of link formation. Conversely, increasing the diameter lowers the aggregate cost of maintaining links but exacerbates the loss of information due to decay. Proposition 1 formalizes this tradeoff by proving that the diameter of any efficient network cannot exceed four. Moreover, when this upper bound is attained, the efficient structure must take the form of a generalized interlinked center-sponsored star , where the most connected agent—referred to as the primary sponsor—acts as an information bridge between other central players, thereby ensuring efficient communication despite the network’s span. See Figure 1 for an illustration.

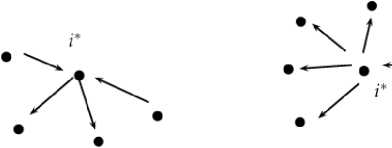
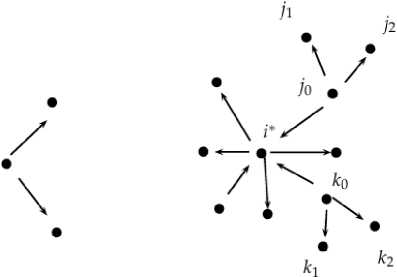
Figure 1. Illustrations of three networks that satisfy Proposition 1 in this paper. Note that the rightmost

NETWORK IS A GENERALIZED CENTER - SPONSORED STAR CONFIGURATION WHERE i * SERVES AS THE BRIDGING AGENT .

Social networks have long been acknowledged as fundamental determinants of economic behavior and social outcomes. For instance, Granovetter’s [2]

seminal work, The Strength of Weak Ties , demonstrated that acquaintances, or weak ties, often serve as vital channels for accessing novel labor

² See paragraph 5 in this introduction for a detailed explanation of player heterogeneity.

market information, while strong ties, such as close friends or family, tend to circulate redundant content. More broadly, network structures influence the diffusion of innovations [3], shape development trajectories [4], and govern the manner in which information propagates through economic systems. These insights have led to the emergence of a robust and interdisciplinary literature on the theory of network formation , which examines how forwardlooking agents strategically decide whom to connect with, balancing the marginal benefits of link creation against its associated costs. One particularly prominent class of networks— Nash or equilibrium networks —arises when agents make linking decisions optimally under Nash equilibrium in pure strategies. This paper contributes to that body of work by extending network formation models to settings that explicitly incorporate heterogeneity across both agents and link-specific costs, drawing on and advancing prior contributions by both foundational and recent studies (e.g., [5]; [6]; [7]; [8]).

The theoretical foundations of modern network formation theory trace back to the influential frameworks developed by [9] and [5]. Jackson and Wolinsky introduced a two-sided link formation model in which the cost of forming a link is split between both agents involved. Their work pioneered the concept of pairwise stability , which highlighted a fundamental tradeoff between network efficiency and individual incentives. In contrast, [5] considered a one-sided cost-sharing model, where only the initiating agent bears the link formation cost. Their analysis, which focused on environments with homogeneous agents, further distinguished between one-way (directed) and two-way (undirected) flows of information. In the one-way case, where only the sender benefits from forming a link, equilibrium structures tend to be efficient and relatively simple, often taking the form of star or wheel configurations. This paper builds on [5]’s framework but modifies it in two important directions: it assumes two-way information flow and allows only the initiating agent to pay the cost, while introducing heterogeneous link costs determined by agent identity.

Subsequent research has sought to relax the assumption of homogeneity. Notably, [10]

incorporated player heterogeneity into the two-way information flow model and demonstrated that under linear payoff functions, efficient and equilibrium networks may coincide. The notion of player heterogeneity refers to the idea that the cost of initiating a link depends on characteristics specific to the sending agent. For instance, if agent i places a call to agent j, the incurred cost may vary depending on i’s mobile service plan or technological capability. While Galeotti et al. showed that Nash and efficient networks can coincide in such linear settings, this alignment breaks down under more general, nonlinear payoff structures. For example, [11] shows that with richer functional forms, efficient networks can exhibit high-diameter configurations such as linear chains, which are often inefficient in practice due to information loss. In contrast, this paper demonstrates that when a natural and empirically plausible small decay assumption is introduced, the set of efficient networks becomes substantially more constrained and also more realistic. Specifically, it identifies a key structural tradeoff: networks with shorter diameters reduce information loss but raise formation costs, while those with longer diameters conserve on cost but suffer from higher information degradation. Proposition 1 sharpens this insight by establishing that no efficient network can have a diameter greater than four. Moreover, when this upper bound is tight, the efficient configuration must be a generalized center-sponsored star in which the most central agent acts as a communication hub bridging other influential nodes. See Figure 1 for an illustration.

The remainder of the paper proceeds as follows. Section 2 formally introduces the model, detailing the payoff structure and defining key conceptual tools such as the efficient transmitter/receiver pair tighten existing results, eliminate unrealistic configurations, and yield more robust characterizations of efficient structures, particularly in settings where information transmission plays a central role.

and the notion of the best-informed agent , which is adapted from the framework in [12]. Section 3 develops these ideas further and presents Proposition 1, which shows the equivalence between these concepts and formally characterizes the class of efficient networks under heterogeneous link costs. Section 4 concludes with a discussion of the paper’s broader implications, unresolved questions, and directions for future research. All technical proofs are provided in the Appendix for completeness and transparency.

It includes the relevance of the research topic, a review of the literature on the research topic, the formulation of the research problem, the formulation of the goal and objectives of the research.

THE MODEL

This note follows the notational conventions established in [12], as it builds directly on that foundational framework. To incorporate player heterogeneity in a consistent manner, it also adopts elements of the notation from [11], which addresses heterogeneity in agent-specific characteristics in a related context.

Agents, Links, and Strategies

Let N = {1,..., n} denote a finite set of agents. Each agent i £ N has the ability to unilaterally form a directed link to any other distinct agent j £ N\{i}, without requiring the consent or cooperation of agent j. A directed link from agent i to agent j is denoted by ij. The collection of all links that agent i can potentially initiate is denoted by L_t = {ij:j Ф i}, and the total set of all possible links in the network is L = ^ ieN ^L i .

A strategy for agent i consists of a subset g_t ^ L_t , which represents the particular links that agent i chooses to form. A complete strategy profile for the network is then represented by g = V [_£n g_t , and the set of all possible network configurations is denoted by G = 2^L . Following standard practice, we use the terms “strategy profile” and “network” interchangeably. The notation ij £ g signifies that agent i has established a link directed toward agent j. For example, if N = {1,2,3} and g = {12,23}, this means that agent 1 links to agent 2, and agent 2 links to agent 3, while agent 3 initiates no links.

Information Flow and Connectivity

Information flows symmetrically within the network: if either ij £ g or ji £ g, then agents i and j can exchange information. We write i] £ g to indicate that such bidirectional information flow occurs between agents i and j. The corresponding undirected information structure is then defined as g = {i]£g:i* j}.

Information can also propagate indirectly through sequences of undirected links, or paths . A path from agent i to agent j, denoted P tj (g'), consists of a sequence of undirected links {1 0 1 1 ,.., i_k - ₁i_k}, where i o = i, i k = j, and each intermediate link is present in g.

Two agents i and j are said to be connected if such a path exists. The length of the shortest path between them defines the distance d tj (g'), measured in the number of links traversed. By convention, we assume du (g) = 0 and set d_t j (g) = ^ when no such path exists. Two networks g¹ and g² are said to share the same information structure if their undirected counterparts g¹ and g² are isomorphic under some relabeling of agents.

Link Costs and Agent Heterogeneity

Each directed link carries a cost borne solely by the sponsoring agent. Let Cy denote the cost incurred by agent i to establish a link to agent j, and let C = {C ij}i*j represent the entire cost structure. When C [j = C for all agent pairs i,j, link costs are said to be homogeneous. In contrast, if c_t j = C for all j, then costs vary across agents but not with respect to the target of the link. This is a case of agent-specific heterogeneity, as considered in [10].

Information Decay and the Small Decay Assumption

As information travels through the network, it gradually decays. We let a £ [0,1] denote the decay parameter, such that each additional link along the transmission path reduces the information value by a factor of a. If the original value of agent j’s information is 1, and the shortest path from agent i to agent j spans к links, then the amount of information agent i receives from j is a^k . The case a = 1 corresponds to a scenario where there is no decay at all.

Throughout this work, we adopt the small decay assumption, following [12], meaning that the decay factor a is assumed to be close to 1. This assumption reflects an environment in which reducing path length yields only marginal informational benefits, and therefore agents are less inclined to form redundant links. As a consequence, efficient networks tend to be minimally connected: that is, there exists at most one path between any two connected agents.

Structural Definitions and Network Operations

A subnetwork g' c g is called connected if every pair of agents in g' is connected by a finite path. A component is a connected subnetwork that is maximal with respect to inclusion. An agent is said to be a singleton if it forms no links and is not connected to any others. A network is minimal if it is connected and contains no cycles.

We also categorize agents based on the direction of their links. An agent is a sender (respectively, receiver ) if it initiates (receives) at least one directed link. A link ij is said to point toward an agent i' if j lies on a path from i to i'; otherwise, it points away.

Minimally connected networks often exhibit recognizable structural patterns. A star network features a central agent i such that Г] E g for all j Ф i, and no other links are present. If all links originate from the center, it is a center-sponsored star . By connecting the centers of multiple stars, one can construct an interlinked star . If each constituent star is center-sponsored, the resulting network is called an interlinked center-sponsored star . An agent that links the centers of two or more stars is referred to as a bridge agent . A generalized interlinked star , as defined in [11, 13], involves a unique bridge agent for each pair of star centers.

Removing an undirected link ij from a minimally connected network results in the network breaking into two distinct components, denoted D^g) and D^g), which contain agents i and j, respectively. The corresponding sets of agents are denoted N ^ (g) and N^j (g). These constructions support a variety of network operations. One may, for example, remove a link (denoted g — ij), add a new link (g + ij), or perform both operations simultaneously (g — ij + kl). If g' and g" are disconnected subnetworks, and i E g', j E g", then g' Ф гу g" denotes their union with an added link ij. A link ij is called a terminal link if its removal isolates agent j, i.e., N^j (g) = {j}, in which case j is called a terminal agent .

Information and Payoffs

Each agent possesses private information with value V. The amount of information that agent i receives from agent j under network g is given by I ij (g) = a^d4⁽³^V. The total information accumulated by agent i is then:

1 1 (g) = Z in ⁽g),

JEN which includes their own information since iu(g) = V.

Agents incur costs only when they initiate links. Let С: K + U {0} ^ K + U {0} be a strictly increasing cost function. Define the set of agents that i links to as N [ ^S(g) = {j E N: ij E g}. Then the total cost incurred by agent i is С (E^s^ c^). The agent’s net payoff is given by:

u_l(g) = i_l(g) — c(E_j EN S (^) C_lj). (1)

In a simplified setting where agents are homogeneous, link costs are linear, and V = 1, the payoff simplifies to:

U t (g} = ^

JEN

aaijW

— n - C,

where n^f = \N $ (g) | is the number of links formed by agent i. In the more general case considered in Proposition 2, we preserve agent heterogeneity and represent the payoff as:

u^g} = 11(g) - C(nfc), without imposing any assumptions on the functional form of C(-), such as convexity or concavity.

Stability and Efficiency

A strategy g j c g * is a best response for agent i if:

Ut(g*) > Ui(gi U g-)  for all gb where g— = g*\g*. A network is a Nash network if every agent adopts a best-response strategy.

The efficiency of a network is evaluated in terms of total social welfare, given by W(g) = E”^ U (g). This can be decomposed as:

n

W⁽g) = ^k ⁽g) 1=1

—Ы z 4

i=1   \jeN?)g   /

^Г(3)             Cg

Here, 1(g) represents the total information benefit in the network, while C(g) represents the aggregate link costs. If two networks g and g’ satisfy n^f(g) = n^f(g’) for all i, then they are link-symmetric equivalent (ls-equivalent), implying they have identical total costs. If T(g') > T(g), then g' is considered an improved network and strictly dominates g in efficiency.

Remark: When the assumptions of agent heterogeneity, small decay, and the general payoff structure outlined above are satisfied, any improved network will dominate the original network in terms of welfare.

Best-Informed Agent

Let M c N be a minimally connected subset of agents. Within M, agent i E M is said to be better informed than agent j E M if:

^ ^ (5) > ^ ^ (^).

кем        кем

If this inequality holds for all j E M, then i is identified as the best-informed agent within M. In cases where M corresponds to the set N f _y(g) obtained by removing a particular undirected link xy, we say that i is the best-informed agent with respect to that link.

his section describes in detail the methods that were used to obtain the results. Usually, the general outline of the study is given first, then they are presented in more detail so that any competent specialist can reproduce them using only the text of the article.

MAIN ANALYSIS

Preliminary Insights and the Proposition

In this section, we present and analyze Proposition 1, which provides a foundational structural characterization of efficient network configurations under a set of three key assumptions. These are: (i) the small decay condition as originally formulated in [12]; (ii) agent-specific heterogeneity in the cost of link formation, as explored in [11] and [10]; and (iii) the presence of a bidirectional flow of nonrival information, consistent with the modeling framework developed by [5]. Under these assumptions, we establish that any network satisfying efficiency criteria must possess a diameter no greater than 4 and must take the form of a generalized interlinked star. This architecture can be interpreted as a two-tiered hub-and-spoke configuration, where a single central agent operates as the primary hub, receiving links from one or more secondary hubs. A graphical illustration of this structure is provided in Figure 2.

To build intuition for Proposition 1, we first provide the conceptual motivation and a set of illustrative examples that bring to light the underlying mechanisms driving the efficiency result. The core idea is intuitive: if a given network structure fails to be efficient, then there must exist an alternative configuration—achievable via a feasible reallocation of links—that delivers strictly higher aggregate welfare while incurring no additional total cost. We refer to any such alternative as an improved network . More formally, we say that network g' improves upon network g if it satisfies the dual condition T(g') >  1(g) and C(g') < C(gf In this case, we say that g' dominates g, since it achieves strictly greater aggregate information flow at equal or lower cost.

Next, consider two networks g and g' with the same set of agents N. We say that g and g' are Is- equivalent if, for every i E N, it holds that n f (g) = n f (g'). For instance, suppose we modify a network g into g — ij + ik, where ij E g and к E N^g). Then, clearly g and g — ij + ik are Is-equivalent, since the only difference between the two networks is that agent i replaces the link ij with a link to another node k. Naturally, if g and g' are Is- equivalent, then they incur the same total cost: C(g') = C(g'). Therefore, if I(g') > 1(g) while g' and g are Is-equivalent, it follows that g' improves upon g.

We offer two examples that concretely illustrate how such improvements may arise through local and minimal structural modifications. The first example shows that network efficiency can be enhanced by making a change to just one link, while the second example shows that a similar welfare improvement can result from modifying two links. These local link replacement procedures are formally captured and generalized in Lemmas 5 and 6, which are provided in the Appendix.

L Hi Hj

network g1

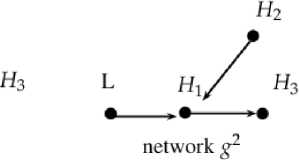
F igure 2. g¹ and g² as in Example 1.

Example 1. Adapted from Example 1 in [11], consider a simple setting involving four agents: one low-cost agent L, and three high-cost agents H1, H2, H3. Assume the parameter values are given by σ = 0.99, V = 100, with link costs cL = 2 for the low-cost agent and cH = 3 for each high-cost agent i. The payoff function for each agent i is specified as: πi(g) = 100 ∑j σdij(g) - nidci2. In the hypothetical absence of information decay (i.e., when σ = 1), both the line network g1 and the star network g2 are efficient om Figure 2 are efficient. These two network structures are said to be ls-equivalent, since g2 is obtained from g1 via a sequence of link replacements that preserve the individual outdegree of each agent: g2 = g1 - H2H3 - H1H2 + H1H3 + H2H1. As a result, the total cost of the two networks is equal: C‾(g1) = C‾ (g2).

However, when we account for even a small amount of information decay, a clear difference emerges. Specifically, the total information in g2 strictly exceeds that of g1, i.e., I(g2) > I(g1), thereby making g2 strictly more efficient. In this configuration, agent H1—who is positioned to become the best informed—receives direct links from both agent L and agent H2, aligning with the efficiency criteria articulated in Proposition 1.

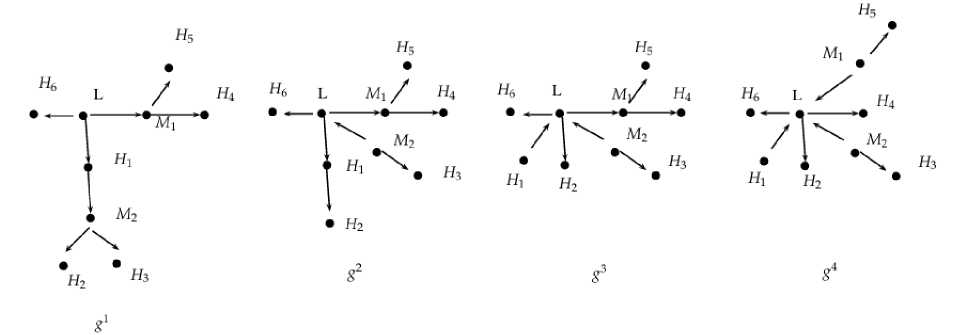
Figure 3. four networks as in Example 2.

Example 2 . Using the same payoff function described above, we now consider a more complex environment with nine agents. These agents are grouped as follows: one low-cost agent L, two midcost agents M₁ and M₂, and six high-cost agents H₁ through H₆ . Assume the cost parameters are c_L = 1.2, c_M = c_M = 1.5, and c_H = 3 for all i ∈ {1,…,6}. In the absence of information decay, as in Figure 3 all four networks g¹ , g² , g³ , and g⁴ are efficient and ls-equivalent, since they preserve the same allocation of link-sponsoring responsibilities: agent L sponsors 3 links, each mid-cost agent sponsors 2, and each high-cost agent sponsors at most 1.

However, once we introduce a small amount of decay into the model, only g4 retains its efficiency. A strict ranking emerges among the networks in terms of their total information values: ‾I(g1) < ‾I(g2) < I(g3) < I(g 4). Each successive transition corresponds to a reallocation of links toward the best-informed agent, which in this case is agent L. This reallocation enhances the total information available in the network without increasing overall costs. Consequently, g4 exemplifies the efficient structure characterized by Proposition 1.

Proposition 1 (Characterization of efficient networks: player heterogeneity case). An efficient network g in the presence of player heterogeneity, under the assumption of small information decay and a payoff structure as specified in Equation 1, contains at most one unique nonempty component. This nonempty component includes a best-informed agent, denoted by i^∗, who satisfies the following two essential properties:

• •    Every agent who sends at least one link must be directly connected to the best-informed agent i^∗ ; that is, for every player i such that the number of links they send, n_i^S(g), is at least one and i ≠ i^∗, it must hold that ii^∗ ∈ g. In other words, all active link senders (excluding i^∗) are directly linked to i^∗ as a recipient, ensuring centralized access to high-quality information.

• •    The agent i * is a largest sponsor in the network. This means that i * sponsors more links than any other player in the component, ensuring maximal dissemination of information from the best-informed node. 4

As a result of these properties, the structure of the unique nonempty component in any efficient network must satisfy the following additional conditions:

• 1.    The diameter of the component is no greater than 4. This constraint ensures that even in the worst-case configuration within the efficient component, the maximum number of steps required to transmit information between any two agents remains bounded and low, preserving informational efficiency.

• 2.    The best-informed agent i * is the only multi-recipient agent in the component. Every link that i * chooses to sponsor leads to a terminal node—that is, a node that does not forward information further. Moreover, any other link in the network, provided it does not end at i * , must also be terminal. This structure prevents the formation of inefficient intermediate relays and ensures that information dissemination is as direct and non-redundant as possible.

• 3.    In the special case where the diameter of the component attains its upper bound of 4, the structure of the efficient component takes the form of a generalized interlinked center-sponsored star. In this configuration, i * plays the role of a bridge agent, serving as the critical intermediary that connects different peripheral clusters and ensures efficient flow of information across the entire network.

DISCUSSION AND RELATION TO LITERATURE

Proposition 1 meaningfully extends and sharpens the earlier findings of [11], who studied efficient network formation under player heterogeneity but assumed the absence of information decay. In their framework, the total information generated by a network remains constant across different configurations, eliminating the possibility of welfare gains through reductions in network diameter. As a result, efficient networks can feature high diameter, such as in the case of line structures. This sharply contrasts with our findings under small decay, where reducing the diameter yields a clear improvement in efficiency.

This distinction underscores a fundamental tension between network efficiency and equilibrium stability. In [11], Nash-stable networks often emerge as stars or disjoint unions of stars, whereas efficient networks may take the form of long chains. To bridge this gap, their analysis invokes restrictive and arguably artificial assumptions regarding payoff structures or cost functions. By contrast, our result demonstrates that even a mild level of decay suffices to eliminate large-diameter networks from the efficient set— without resorting to any such strong assumptions. Thus, incorporating even a modest degree of decay offers a more intuitive and parsimonious resolution to the well-known efficiency-stability tradeoff in network formation.

This section presents experimental or theoretical data obtained during the study. The results are given in the processed version: in the form of tables, graphs, organizational or structural diagrams, equations, photographs, drawings. This section contains only the facts. Leave their interpretation, comparison with the data of other researchers for the Discussion section.

CONCLUSION

In this note, I have provided a rigorous and detailed characterization of efficient network structures under the dual assumptions of agent heterogeneity and small levels of information decay. The central result, formalized in Proposition 1, shows how these assumptions allow for a clear understanding of the tradeoff between maximizing total information flow and limiting unnecessary cost through shorter network paths. In particular, the assumption of small decay enables us to rule out large-diameter structures as efficient, streamlining the set of efficient networks to those with more centralized and hierarchical architectures.

It is worth reiterating that this analysis adheres to the standard assumption in the literature on information networks: an agent’s utility is determined by the total amount of information they receive within the network. To the best of my linking. The equivalence between these two concepts only arises under specific additional assumptions, such as those imposed in Proposition 5 of (3).

knowledge, existing studies on efficient networks have not significantly departed from this modeling approach to explore more general or nonlinear benefit structures. Accordingly, a promising direction for future research would be to examine how the nature of efficient networks might change under alternative utility specifications, especially those that allow for diminishing returns or agent-specific valuations of information.