Экспериментальное определение модового состава излучения, распространяющегося в многомодовом оптическом волокне

Использование многомодовых волокон в оптических линиях передачи (по сравнению с маломодовыми волокнами) имеют большие преимущества, так как позволяют передавать большой объем информации, кроме того, распространение в волокне нескольких мод делает возможным параллельную передачу данных. Особенно перспективно использование многомодовых волокон для пространственного модового мультиплексирования [1], параллельной передачи данных [2] и передачи изображения через волокно [3]. Важнейшим вопросом при разработке и исследовании многомодовых систем связи является разложение излучения, распространяющегося в оптическом волокне, по модам. Существуют множество методов определения модового состава излучения оптического волокна (например, [4-6]), но до настоящего момента нет метода экспериментального анализа модового состава излучения многомодовых волокон с произвольными параметрами.

В данной работе предлагается метод определения модового состава излучения, распространяющегося в оптическом волокне, в основе которого лежит разложение комплексного светового поля по неортогональным модам. Рассмотрим распространение света в оптическом волокне со ступенчатым профилем показателя преломления. В приближении слабонаправляющего волновода можно записать четыре поляризационные моды в поперечном сечении на длине z для любого значения орбитального момента т ( т >  0) и радиального квантового числа N [7]:

Mm)N(x’У’z) = [cos(mФ)ex — sin(mФ)ey ] • Fm,N(x’У) • ei^’N

M mN ⁽ x ’ У ’ z ) = ^{[cos( m} Ф ^{) e} x + ^{sin( m} ^ ) e y ^] • F m , N ⁽ x ’ У ) • e z³™’ N

MmN (x’У’ z) = [sin(mФ)ex + cos(mФ)ey ] • Fm,N (x’У) • e^m'"

M mN ⁽ x ’ У ’ z ) = ^{[sin( m} Ф ^{) e} x ^{- cos( m} Ф ^{) e} y ^] • F m , N ⁽ x ’ У ) • e i ^ m ^N

Здесь e x , e_y - собственные вектора, ф = arctg( x/ y ), F_mN ( x , y ) - функции Бесселя, P k _N - постоянные распространения, определяющие скорость распространения мод.

Разложение произвольной функции по системе неортогональных функций является классической задачей функционального анализа [8]. Разложим электрическую составляющую светового поля E ( x , у ), распространяющегося в оптическом волокне, представив в виде суперпозиции поляризационных мод M m n ( x , у ):

E ( x , У ) = ZZZ C k , N M m,N ( x , У )

k = 1 т N

Большаков М.В., Комарова М.А.,   Экспериментальное определение модового состава излучения,

Кундикова Н.Д.                   распространяющегося в многомодовом оптическом волокне где постоянные Ck - комплексные коэффициенты при различных поляризационных модах. Для m, N удобства перейдем к сквозной нумерации мод: вместо индексов k, m, N введем индекс i = 0... (L -1), где (L -1) - полное количество мод, распространяющихся в оптическом волокне. Перепишем выражение (2):

E ( x , у ) = £ C i M i ( x , у ),                                  (3)

i постоянные Ci называются коэффициентами разложения функции светового поля E(x, у) в базисе функций {Mi (x,у)}. Базис {Mi (x,у)} не удовлетворяет условию ортогональности

( M i ( x , у ), M j ( x , у )) Ф 0 при i Ф j ;

где функционал скалярного произведения определяется выражением

( a , b ) = jj a ( x , у ) b ( x , у ) dxdy .

Распределение поля каждой моды M i ( x , у ) определяется из выражений (1). Суммарное световое поле E ( x , у ) известно из эксперимента. Таким образом, коэффициенты разложения C i по неортогональной системе функций определяются системой линейных уравнений

L - 1

£ C_; ( M i , M j ) = ( E , M j ), j = 0, ^ ,( L - 1).                         (4)

i = 0

Такая система получается в результате скалярного умножения (3) на систему базисных функций {Mi (x,у)}. Матрица системы (4) состоит из попарных скалярных произведений базисных функций. Решая полученную систему, можно получить коэффициенты Ci . Для расчета ком- плексных коэффициентов ci была написана программа в пакете MATLAB. Для апробации модели определения модового состава излучения сначала была проведена серия расчетов с теоретически заданным распределением поля. Генерировался случайно заданный модовый состав излучения Ci на входе в волокно, рассчитывалось распределение поля на выходе из волокна E(x, у). Распределение поля каждой моды Mi (1) определяется параметрами волокна и длиной волны света. Составлялась система линейных уравнений (4), решением которой были комплексные коэффициенты Ci = Ca exp(iC^,), здесь C; - амплитудные коэффициенты, C± - фазовые коэффи- циенты. Проверка осуществлялась сравнением рассчитанных комплексных коэффициентов Ci с генерированными изначально. Тестовые расчеты проведены для волокна со следующими параметрами: показатель преломления сердцевины nco = 1,47, числовая апертура Na = 0,11, радиус сердцевины волокна r = 6 мкм, длина волокна z = 20 см, длина волны света X = 0,633 мкм. В оптическом волокне с данными параметрами для данной длины волны света распространяются семь поляризационных мод Mi (x, у).

В результате тестирования обнаружено, что для m > 0 погрешность определения коэффициентов составляет 0,001 %, однако для m = 0 коэффициенты отличались от заданных. Данные результаты можно объяснить тем, что для m = 0 распределение поля MkN является аксиально симметричным и находятся несколько наборов модовых коэффициентов, удовлетворяющих условию. Таким образом, модовые коэффициенты для m = 0 являются вырожденными. Полученные распределения интенсивностей с рассчитанными коэффициентами полностью идентичны распределениям интенсивности с заданными коэффициентами, среднеквадратичное отклонение распределений интенсивности порядка 10-12. Таким образом, была решена задача определения модового состава излучения по теоретическому распределению поля на выходе из волокна. По- грешность метода составила 0,001 %.

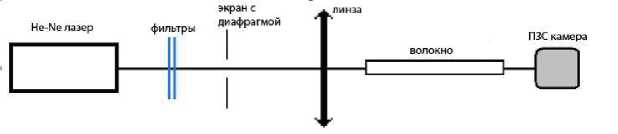
Рис. 1. Оптическа^ схема экспериментальной установки

В эксперименте информацию о комплексном световом поле, распространяющемся в оптическом волокне, невозможно получить прямыми из-

Краткие сообщени^

мерениями. Данная информация может быть получена с помощью алгоритма Гершберга– Сэкстона [9], который позволяет восстанавливать поле по двум распределениям интенсивностей в ближнем и дальнем полях. Для получения информации о комплексном световом поле регистрировалось распределение интенсивности на выходе из волокна в ближней и дальней зоне. Схема экспериментальной установки представлена на рис. 1.

Излучение He-Ne лазера с длиной волны λ = 0,633 мкм, ослабленное фильтром, проходило через экран с диафрагмой и фокусировалось на торец оптического волокна тонкой собирающей линзой с фокусным расстоянием f = 2 см. Для экспериментальных исследований использова- лось оптическое волокно с диаметром сердцевины 9 мкм и длиной 50 см. После прохождения через волокно свет попадал на активный элемент ПЗС камеры с размером чувствительной области 5,2х3,9 мм. Таким образом, регистрировалось распределение интенсивности в дальнем поле.

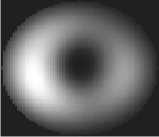
Для получения распределения интенсивности в ближнем поле между выходным торцом волокна и активным элементом ПЗС камеры устанавливался 40-кратный объектив с числовой апертурой 0,65. Зарегистрированные распределения интенсивности на выходе из волокна в ближнем и дальнем полях представлены на рис. 2.

Рис. 2. Распре^елени^ интенсивностей в бли^нем (а) и ^альнем (б) пол^х

Распределения интенсивности в ближнем и дальнем поле использовались для восстановления фазы комплексного светового поля в ближней зоне, т.е. на торце волокна, на основе алгоритма Гершберга–Сэкстона. Моделирование осуществлялось в пакете MATLAB с использованием итерационной процедуры с быстрым преобразованием Фурье, восстановленное фазовое распределение представлено на рис. 3, б. Погрешность метода составила 6,7∙10–15, по- грешность рассчитывалась как среднеквадра тичное отклонение между текущим амплитудным распределением и исходным экспериментальным распределением дальнего поля на конечной итерации.

Таким способом была получена информация о комплексном световом поле на выходном торце волокна. Задача определения модового состава излучения решалась разложением комплексного светового поля, распространяющегося в оптическом волокне, на выходном торце волокна по неортогональным модам. В целом экспериментальный метод определения модового со- става излучения отличается от теоретического метода только тем, что в теоретическом методе известны заданные коэффициенты, с которыми впоследствии осуществляется сравнение. Для определения модового состава излучения по экспериментальному распределению поля на выходном торце волокна распределение поля раскладывалось по неортогональным модам и составлялась система линейных уравнений (4). В оптическом волокне с данными параметрами и длиной волны света распространяются четыре поляризационные моды M i . Решение системы линейных уравнений (4) позволило получить комплексные коэффициенты Ci при модах Mi (см. таблицу).

Амплиту^ные коэффициенты C ⁺ , C ^- и фазовые коэффициенты C ⁺ , C ^- ^л^ ка^^ой из пар m , N a a                ϕϕ

m	N	+ Ca	C ϕ +	- Ca	C ϕ -
0	1	0,0174	–2,7155	0,0174	2,3159
0	2	0,0096	–1,9498	0,0096	1,5688
1	1	0,8848	–0,4625	1,0000	–0,1677
2	1	0,0200	0,5680	0,0622	0,2955

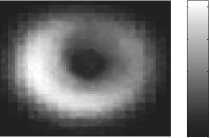
Экспериментально измеренное и рассчитанное с вычисленными коэффициентами распределения интенсивности на выходном торце волокна представлены на рис. 3. Из рис. 3 видно, что наблюдается хорошее соответствие между экспериментально зарегистрированным и рассчитанным распределением интенсивности.

Таким образом, предложен и реализован метод, позволяющий определить модовый состав излучения, распространяющегося в многомодовом оптическом волокне, по известному распреде-

Большаков М.В., Комарова М.А., Экспериментальное определение модового состава излучения, Кундикова Н.Д. распространяющегося в многомодовом оптическом волокне лению поля на выходном торце волокна. Получено хорошее соответствие между экспериментально зарегистрированными и рассчитанными распределениями интенсивности и фазы.

20      40      60

x, пиксель

б

10 20 30 40 50 60

x, пиксель

-2

20      40      60

x, пиксель

-2

10 20 30 40 50 60

x, пиксель

Рис. 3. Распределения интенсивности и фазы: рассчитанное с вычисленными коэффициентами (а), экспериментально измеренное (б)