Экспериментальное определение увода оси отверстий при обработке зенкером с МНП

Разработана математическая модель (1), которая учитывает фактические значения площадей срезаемых каждым лезвием сечений припуска Δ1, Δ2 и Δ3, возникающих из-за погрешностей заточки и сборки лезвий зенкера с многогранными неперетачиваемыми пластинами (МНП) [1, 2]. Это приводит к различным значениям сил резания, действующих на каждое лезвие, и к поперечным смещениям оси инструмента во время обработки отверстия. Следствием этого является разбивка (разница между диаметрами обработанного отверстия и инструмента) и увод оси отверстия [3–7]. Для проверки адекватности математической модели были проведены натурные и компьютерные эксперименты.

⁴¹ = (' pitu^zs : ^ • g + (tg(₉₀ - _ф1) • „_1W _ 4^.

■ А2 = (^P~" ~1"""" ^Z"^ • [ | + 1 + tgt^ - Ф 1 ) • (р2(Ф + 120 » ) -"~)].                      (1)

A3 = ( . .^^ • [_($ - ( 25 + _т) + 1 ) + tg(_V3 - _ф2) • (р3(ф + 240 » ) - 2 ? )].

где Δ1, Δ2, Δ3 – площади сечения припуска срезаемых соответственно 1, 2 и 3-м лезвиями зенкера; ρ1(ψ), ρ2(ψ + 120°), ρ3(ψ + 240°) – радиус-векторы соответственно 1, 2 и 3-го лезвий зенкера;

ψ – текущий угол поворота зенкера вокруг своей оси; φ1, φ2, φ3 – главные углы в плане соответственно 1, 2 и 3-го лезвий зенкера с учетом погрешностей заточки или уст а новки лезвий; S – подача инструмента; d 0 – диаметр отверстия в заготовке.

Радиальные составляющие сил резания Р1, Р2 и Р3, действующие на каждое лезвие зенкера, определяются по зависимостям [8–11]:

Р1 = Δ1 К1, Р2 = Δ2 К2, Р3 = Δ3 К3, (2) где К1, К2 и К3 – коэффициенты пропорциональности сил резания площад я м срезаемых сечений, учитывающие свойства обрабатываемого и инструментального материалов, геометри ю режущей части инструмента и др. [12, 13].

Как показали исследования [1, 2], основной причиной возникновения увода оси отверстия являются осевые биения инструмента, возникающие от осевых колебаний ш пинделя с т анка. Это приводит к колебаниям подачи S , которая будет изменяться по следующей зависимост и

S = S0 ΔS cos(ψ), (3) где S0 – номинальное значение подачи инструмента; ΔS – амплитуда колебаний подачи или шпинделя станка.

Сравнение расчетных значений площадей срез а емых сечений (1) показало, что на разных лезвиях величина площадей Δ1, Δ2 и Δ3 может различаться до 25 раз. Следовательно, и силы резания (2) будут различаться во столько же раз.

Поскольку Р1 ≠ Р2 ≠ Р3, то возникает результи р ующая сила Σ P, приводящая к поперечным смещениям зенкера, т. е. к уводу оси отверстия. Ре з ультирующая сила [14–19] определяется за каждый оборот инструмента по правилам сложения в екторов (рис. 1). Увод оси отверстия Δу определяется по формуле

ДУ = j , (4)

где j – жесткость инструмента.

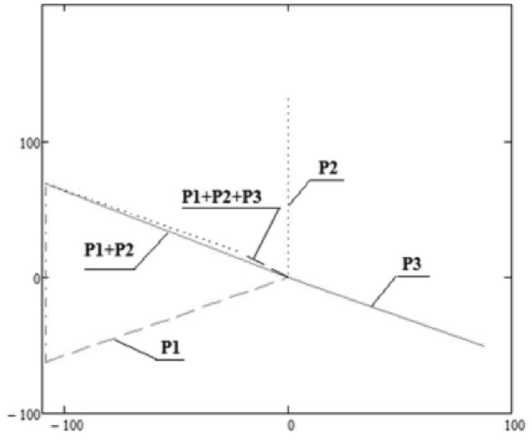
Рис. 1. Сложение векторов сил резания

Для проведения экспериментов выбран трехлезвийный зенкер с МНП (рис. 2), обработка производилась на обрабатывающем центре ММ800 Fanuc [20]. Измерения обработанных де т алей производилось:

• 1)    в системе Renishaw с т очностью позиционирования п о осям X, Y, Z – ± 0,005 мм, повторяемость X, Y, Z – ± 0,003 мм;

• 2)    с применением аддитивных технологий на основе 3D-сканера производителя Range Vision Spectrum (рис. 3), это сканер высокого разрешения, работает по принципу структурированного света. Погрешность его сост а вляет 0,001 мм для деталей до 300 мм п ри измере н ии линейных и диаметральных размеров.

Эксперимент заключался в обработке заготовок (рис. 4) из стали 40Х, алюминия АМЦ и нержавеющей стали 12Х18Н9.

Методика проведения натурного эксперимента следующая:

• •    Сверлится сквозное отверстие в металле.

• •    Зенкером с МНП производится чистовая обработка отверстия.

• •    Во время обработки отверстия зенкером с МНП производится мгновенный остан о в станка.

• •    Производятся замеры увода оси отверстия в системе Renishaw.

• •    Производятся замеры с помощью 3D-сканера.

Основные параметры проведения эксперимента показаны в табл. 1.

После обработки образцов деталей были произве д ены замеры увода оси отверстия.

Схема замеров в системе Renishaw с применением компактного датчик а показана на рис. 5.

Параметры эксперимента

Таблица 1

№ детали	Материал	Параметры обработки
1, 2	Сталь 40Х	– диаметр сверла – 18,5 мм; – диаметр зенкера – 20 мм; – частота вращения инструмента – 300 об/мин; – подача инструмента S = 0,12 мм/об; – глубина обработки – 8 мм
3, 4	Алюминий АМЦ
5, 6	Сталь 12Х18Н9

Рис. 2. Зенкер с тремя МНП

Рис. 3. Range Vision Spectrum

Рис. 4. Обработанные заготовки

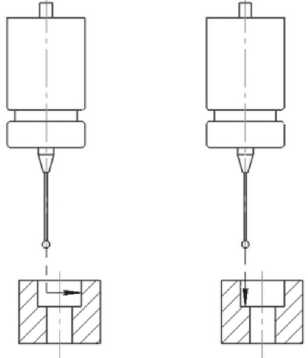
Рис. 5. Схема контроля системой Renishaw

Далее производились замеры с помощью 3D-сканера. Данный 3D-сканер, направляет проекцию световой сетки непосредственно на объект, деформация этого рисунка и представляет собой модель сканируемого предмета. Сетка проецируется на объект с помощью жидкокристаллического проектора или другого постоянного источника света. Камера, расположенная чуть в стороне от проектора, фиксирует форму сети и вычисляет расстояние до каждой точки в поле зрения. 3D-сканеры создают облако точек, которые могут напрямую использоваться для измерений или визуализации в области архитектуры и конструирования. Покажем основные этапы измерения увода оси отверстия.

Каждую деталь проверили на увод оси отверстия в области работы зенкера в ПО GeomagicX. Выполняем разбиение на области, для того чтобы разобрать скан детали на элементы. Разбиение показано на рис. 6.

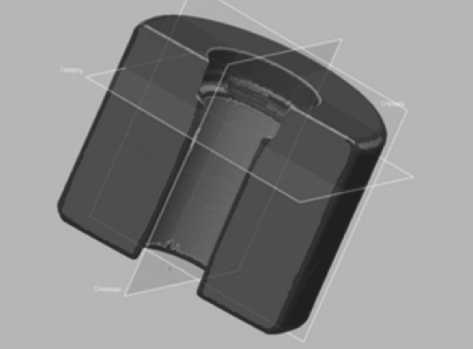
Рис. 6. Разбиение на области

Рис. 7. Выравнивание детали

Следующий этап – это выравнивание детали относительно системы координат (рис. 7).

Далее выполняем 2 эскиза для определения центра окружности и диаметра. Потом с помощью измерения мы можем определить увод центра относительно двух эскизов отверстий (рис. 8).

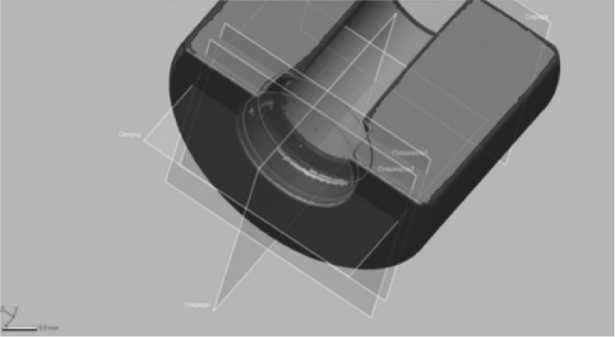
Рис. 8. Выполнение 2 эскизов

Затем выполняем измерение увода оси отверстия обработанного зенкером с МНП по координате (рис. 9).

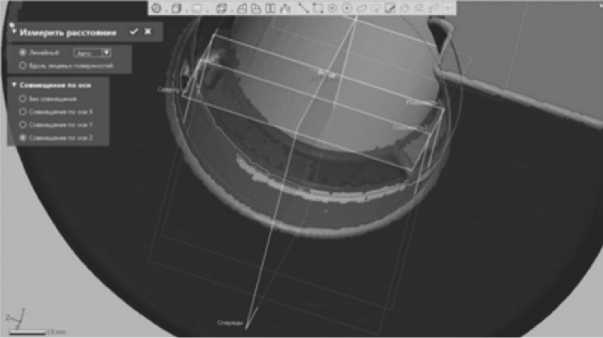
Рис. 9. Измерение увода оси по Z

Аналогично произведем измерение по координате Y. Далее определяется результирующее значения увода оси отверстия.

Используя математическую модель (1) и разработанную на ее основе компьютерную модель, выполнили компьютерные эксперименты. Исходными данными компьютерных экспериментов были параметры обработки (см. табл. 1). В результате были получены теоретические результаты увода оси отверстия.

Результаты натурных и компьютерных экспериментов приведены в табл. 2.

Таблица 2

Сравнение результатов увода оси отверстий

№ детали	Увод оси отверстия, мм
	Математическая модель	Renishaw	3D-сканер
1	0,01592	0,016	0,016
2	0,0124	0,0125	0,013
3	0,0214	0,0216	0,022
4	0,00447	0,005	0,005
5	0,009	0,009	0,01
6	0,01147	0,0115	0,012

Заключение

Сравнивая полученные расчетные значения с экспериментальными (табл. 2), видим, что разница между ними не более 2 %. Следовательно, данная математическая модель адекватна и ее можно использовать технологам при проектировании и компьютерной отладке технологических процессов обработки отверстий зенкерами с МНП [16–20].