Экспоненциальное сглаживание динамического ряда числа разжижения кукурузной крахмалистой смеси

Как известно, «анализ временных рядов -совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и их прогнозирования… Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда...» [1]. Очевидно, что «...выбор метода решения задачи прогнозирования определяется существенными его характеристиками - сложностью задачи и ее обширностью. Так, при решении задач прогнозирования первого уровня сложности и обширности процесса применяют экстраполяционный метод уровня обширности и сложности - экспоненциальное сглаживание , позволяющий получить краткосрочный прогноз...» [2].

Для решения статистических задач достоверность разработанных прогнозов во многом определяется тем, насколько правильно выбран метод прогнозирования, иначе говоря, для получения достоверных прогнозов вначале необходимо определить метод прогнозирования, соответствующий специфике объекта прогнозирования. «…Классический подход к прогнозированию рядов основан на выборе подходящей теоретической модели тренда с неизвестными параметрами, ее параметрической идентификации по данным наблюдения ряда и последующем использовании модели для экстраполяции ряда на период прогнозирования...» [3].

«…Главное достоинство модели прогнозирования, основанной на экспоненциальной скользящей средней, заключается в том, что она способна адаптироваться к новому уровню процесса без значительных реакций на случайные отклонения. Однако данная модель дает значительную ошибку в случае, когда ряд имеет трендовую составляющую. Специально для этого случая существует несколько адаптивных моделей экспоненциального сглаживания... [4]. Моделирование заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону. В таком случае, среднюю называют экспоненциальной средней , которая является характеристикой последних значений ряда динамики, которым присваивается наибольший вес [3].

В анализе технологических процессов «…экспоненциальное cглаживание при текущем предупредительном контроле в отличие от анализа экономических показателей имеет ряд особенностей: одной из них является отсутствие надобности в определении длительного прогнозирования, другой - необходимость учета погрешностей измерения… Поскольку при текущем предупредительном контроле основной целью является быстрое обнаружение резкого изменения процесса, то алгоритм расчета базируется на результатах краткосрочного (на один шаг вперед) прогнозирования» [5].

При необходимости описания текущего состояния процесса без составления прогноза вначале прибегают к вычислению таких статистических показателей динамического ряда, как абсолютный цепной и базисный прирост, цепной и базисный темп прироста, темп наращивания и т. п. Так, абсолютный прирост определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации и рассчитывается по цепному и базисному приростам [6]:

• -    цепной прирост:

А У ц = У ^- У_м            (1)

• -    базисный прирост:

^А У б = У ^- У 1            ⁽²⁾

Темпы прироста характеризуют абсолютный прирост в относительных величинах, а вычисляемый в процентах темп показывает, на сколько процентов изменяется сравниваемый уровень с уровнем, принятым за базу сравнения. Как и абсолютный прирост, подразделяется на цепной и базисный:

• -    цепной темп прироста:

Т прц =А у i / У -1            (³)

• -    базисный темп прироста:

^тпрб =^А У^/ У 1               ⁽⁴⁾

Распространенным в статистике показателем динамики является темп роста, характеризующий отношение двух уровней ряда и выражающийся в виде коэффициента или в процентах, вычисляется цепным или базисным: - цепной темп роста:

Тц yJ У м            ⁽⁵⁾

• -    базисный темп роста:

^т рб = У б/ У 1              ⁽⁶⁾

Абсолютное значение  1%  прироста равно: цепной: 1% ц, = у, - 1 / 100%; базисный: 1%б = у б /100%.

Статистическим показателем динамики в условиях интенсификации изучаемого процесса является темп наращивания, который измеряет наращивание потенциала процесса во времени:

T =^А У ц / У 1              (7)

Средний уровень интервального ряда у динамики характеризует типическую величину абсолютных уровней и рассчитывается по формуле:

У = ^ y

n

Средний темп роста вычисляется как:

T p = n^-

Средний темп прироста равен разности:

T np = T p 1 (10)

Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики:

dy = y У (11)

n –1

Экспоненциальная средняя вычисляется по рекуррентной формуле:

S_t = а х Y_t + ( 1- а ) х S, (12) где S t - значение экспоненциальной средней в момент t; S ц - значение экспоненциальной средней в момент ( t = 1); начальный параметр S 0 берут или равным значению первого уровня ряда у 1 , или равным средней арифметической нескольких первых членов ряда; Y t - значение экспоненциального процесса в момент t; а - вес t -ого значения ряда динамики (или параметр сглаживания).

Последовательное применение формулы (12) дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики. Наиболее важной характеристикой в этой модели является параметр сглаживания а , по величине которой практически и осуществляется прогноз. В случае, если а близко к единице, то в прогнозе существенно учитывается величина ошибки последнего прогнозирования. При малых значениях а прогнозируемая величина близка к предыдущему прогнозу.

Если а близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т. е. при прогнозе учитываются все прошлые уровни ряда. Обычно на практике значение а находится в пределах от 0,1 до 0,3, почти никогда не превышая значение 0,5 [7].

Базовое уравнение имеет следующий вид:

S t = S t х ( 1- а ) + а х Y t (13) где S (t) - это прогноз, сделанный в момент времени t .

Стандартная ошибка (погрешность) рассчитывается по формуле:

e t	т ( y, - S^ , ) 2	(14)
	n –1

где i = (t - 2, t ).

Специалисты отмечают [8], что разжижение крахмала является ключевым этапом в промышленном производстве сиропов. Для повышения эффективности этого процесса было проведено исследование влияния концентрации кукурузного крахмала на ход желатинизации и разжижения. Как показали опыты, повышенные концентрации крахмала (свыше 45%) вызывают ингибирование набухания и разрушение гранул крахмала и приводят к сохранению кристалличности крахмала после термической обработки, что связывают с протеканием неполной желатинизации, вызванной низкой подвижностью молекул воды и полимерных цепей.

Целью данной работы явилось проведение экспоненциального сглаживания динамического ряда числа разжижения кукурузной крахмалистой смеси, состоящей из кукурузной муки тонкого помола и кукурузного амилопектинового крахмала. В исследовании представлена последовательность наблюдений показателя числа разжижения, упорядочиваемого в зависимости от повышения дозировки амилопектинового кукурузного крахмала в кукурузной крахмалистой смеси.

Материалы и методы

Число разжижения для кукурузной крахмалистой смеси, состоящей из кукурузной муки тонкого помола [9] и кукурузного амилопектинового крахмала [10] в соотношении: 100:0, 90:10, 80:20, 70:30, 60:40, 50:50, 40:60, 30:70, 20:80, 10:90, 0:100 получали расчетным путем. Для расчета числа разжижения кукурузной крахмалистой смеси использовали опытные данные числа падения, определяемого по стандартному методу [11], сущность которого заключается в достижении быстрой клейстерилизации водной суспензии муки или цельносмолотого зерна в кипящей водяной бане и последующем определении степени разжижения альфа-амилазой крахмала, содержащегося в пробе. Например, с требуемым значением числа падения подбирают мучные хлебопекарные смеси [12, 13], если число падения перевести в число разжижения. Расчеты статистических показателей динамического ряда числа разжижения без составления прогноза и вычисление его экспоненциальной средней производились с помощью интернет-ресурсов [6, 7], визуализация вычислений прогнозных значений в приложении MS Ехсе1 2007.

Результаты

Цепные показатели ряда динамики числа разжижения кукурузной крахмалистой смеси представлены в таблице 1. Расчеты показывают, что при 100%-ном содержании амилопектинового кукурузного крахмала в смеси число разжижения, по сравнению с содержанием в 90%, увеличивается на 72 ед. или на 33,6%. Максимальный прирост числа разжижения (на 72 ед.) наблюдается при максимальной дозировке амилопектинового кукурузного крахмала в смеси, т. е. 100%. Минимальный прирост числа разжижения (на 3 ед.) зафиксирован при 20%-ной дозировке амилопектинового кукурузного крахмала в смеси.

Таблица 1.

Цепные показатели ряда динамики числа разжижения

Table 1.

Chain exponents of the liquefaction number dynamics series

Дозировка амилопектинового крахмала, % Dosage of amylopectin starch,%	Число разжижения, единиц Number of liquefaction units	Абсолютный прирост Absolute increase	Темп прироста, % Rate of increase, %	Темпы роста, % Growth rate, %	Абсолютное содержание 1% прироста Absolute content of 1% increase	Темп наращения, % Rate of build-up, %
0	15	–	–	100	–	0
10	19	4	26.67	126.67	0.15	26.67
20	22	3	15.79	115.79	0.19	20
30	30	8	36.36	136.36	0.22	53.33
40	71	41	136.67	236.67	0.3	273.33
50	82	11	15.49	115.49	0.71	73.33
60	141	59	71.95	171.95	0.82	393.33
70	160	19	13.48	113.48	1.41	126.67
80	200	40	25	125	1,6	266.67
90	214	14	7	107	2	93.33
100	286	72	33.64	133.64	2.14	480
Итого | Total	1240

Темп наращения показывает, что тенденция динамического ряда числа разжижения возрастающая, что свидетельствует об ускорении роста параметра. Базисные показатели ряда динамики числа разжижения представлены в таблице 2. В смеси, содержащей 100% амилопектинового кукурузного крахмала, по сравнению со смесью с 0%-ным содержанием амилопектинового кукурузного крахмала число разжижения увеличилось на 271 ед. или на 1806,7%. Сводные данные ряда динамики числа разжижения приведены в таблице 3.

Таблица 2.

Базисные показатели ряда динамики числа разжижения

Table 2.

Basic indicators of a number of dynamics of the liquefaction number

Дозировка амилопектинового крахмала, % Dosage of amylopectin starch, %	Число разжижения, единиц | Number of liquefaction units	Абсолютный прирост Absolute increase	Темп прироста, % Rate of increase, %	Темпы роста, % Growth rate, %
0	15	–	–	100
10	19	4	26.67	126.67
20	22	7	46.67	146.67
30	30	15	100	200
40	71	56	373.33	473.33
50	82	67	446.67	546.67
60	141	126	840	940
70	160	145	966.67	1066.67
80	200	185	1233.33	1333.33
90	214	199	1326.67	1426.67
100	286	271	1806.67	1906.67
Итого | Total	1240

Средний уровень интервального ряда y динамики числа разжижения равен: y = Z yjn = 1240/11 =112,73. Соответственно, среднее значение числа разжижения между 0%-ной и 100%-ной дозировками амилопектинового крахмала в смеси составило 112,73 ед.

Таблица 3.

Сводная таблица данных ряда динамики числа разжижения

Summary table of data on the dynamics of the liquefaction number

Table 3.

Дозировка амилопектинового крахмала, % Dosage of amylopectin starch, %	s £ о §	Абсолютный прирост Absolute increase		Темп роста Growth rate, %		Темп прироста Rate of increase, %		Абсолютное содержание 1% прироста Absolute content of 1% increase
		цепной	базисный	цепной	базисный	цепной	базисный
0	15	–	–	100	100	–	–	–
10	19	4	4	126.67	126.67	26.67	26.67	0.15
20	22	3	7	115.79	146.67	15.79	46.67	0.19
30	30	8	15	136.36	200	36.36	100	0.22
40	71	41	56	236.67	473.33	136.67	373.33	0.3
50	82	11	67	115.49	546.67	15.49	446.67	0.71
60	141	59	126	171.95	940	71.95	840	0.82
70	160	19	145	113.48	1066.67	13.48	966.67	1.41
80	200	40	185	125	1333.33	25	1233.33	1.6
90	214	14	199	107	1426.67	7	1326.67	2
100	286	72	271	133.64	1906.67	33.64	1806.67	2.14

Средний    темп    роста    равен:

Tp = п^ УЛУ = 1^ 286/15 = 1,3428. В среднем за весь период рост анализируемого показателя составил 1,3428.

Средний темп прироста равен:

T = T —1=1,3428 -1 = 0,343. В среднем число npp разжижения с каждым интервалом увеличивалось на 34,3%.

Средний абсолютный прирост равен: dy = ( У п — У )/( n — 1 ) = (286 —15)/10 = 27,1. С ^каждым интервалом динамического ряда число разжижения в среднем увеличивалось на 27,1.

Параметр α вычислялся как: α = 2/(21 + 1) = = 0,0909. В качестве S 0 брали первое значение ряда, S 0 = y 1 = 15. Для экспоненциального сглаживания динамического ряда числа разжижения дополнили данные наблюдений (таблица 4) с шагом 5 ед.

S (t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t : S (21+1) = 280,854 (1 – 0,0909) + + 0,0909×286 = 281,322. Стандартная ошибка

(погрешность) равна: е, = /Х ( y \  ) 2 ( п 1 )

=   67,29/ ( 21-1 ) = 1,834

Таблица 4.

Экспоненциальная средняя динамического ряда числа разжижения

Exponential average of the dynamic series of the liquefaction number

Table 4.

t	y	S t	Формула | Formula	(y – S t )2
0	15	15	(1 – 0.0909)×15 + 0.0909×15	0
5	17	16.818	(1 – 0.0909)×17 + 0.0909×15	0.0331
10	19	18.802	(1 – 0.0909)×19 + 0.0909×16.82	0.0393
15	20	19.891	(1 – 0.0909)×20 + 0.0909×18.8	0.0119
20	22	21.808	(1 – 0.0909)×22 + 0.0909×19.89	0.0367
25	25	24.71	(1 – 0.0909)×25 + 0.0909×21.81	0.0842
30	30	29.519	(1 – 0.0909)×30 + 0.0909×24.71	0.231
35	41	39.956	(1 – 0.0909)×41 + 0.0909×29.52	1.089
40	71	68.178	(1 – 0.0909)×71 + 0.0909×39.96	7.963
45	77	76.198	(1 – 0.0909)×77 + 0.0909×68.18	0.643
50	82	81.473	(1 – 0.0909)×82 + 0.0909×76.2	0.278
55	107	104.68	(1 – 0.0909)×107 + 0.0909×81.47	5.384
60	141	137.698	(1 – 0.0909)×141 + 0.0909×104.68	10.9
65	148	147,064	(1 – 0.0909)×148 + 0.0909×137.7	0,877
70	160	158.824	(1 – 0.0909)×160 + 0.0909×147.06	1.383
75	185	182.621	(1 – 0.0909)×185 + 0.0909×158.82	5.662
80	200	198.42	(1 – 0.0909)×200 + 0.0909×182.62	2.496
85	207	206.22	(1 – 0.0909)×207 + 0.0909×198.42	0.608
90	214	213.293	(1 – 0.0909)×214 + 0.0909×206.22	0.5
95	231	229.39	(1 – 0.0909)×231 + 0.0909×213.29	2.591
100	286	280.854	(1 – 0.0909)×286 + 0.0909×229.39	26.479
				67.29

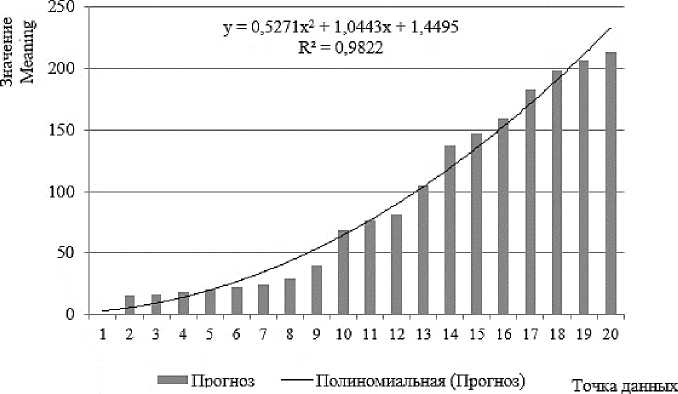
Для визуализации вычисления каждого прогноза в MS Ехсеl использовали отдельную, но алгебраически эквивалентную формулу (таблица 5). Оба компонента – данные предыдущего наблюдения и предыдущий прогноз – каждого прогноза умножали на коэффициент, отображающий вклад данного компонента в текущий прогноз (рисунок 1).

Таблица 5.

Расчет экспоненциального сглаживания динамического ряда числа разжижения в MS Ехсеl 2007

Table 5.

Calculation of exponential smoothing of the dynamic series of the liquefaction number in MS Excel 2007

t	y	Сглаженные уровни | Smoothed levels	Стандартные погрешности | Standard errors
0	15	15	#Н/Д
5	17	16.8182	#Н/Д
10	19	18.80167	#Н/Д
15	20	19.89107	1.843569
20	22	21.8083	1.883597
25	25	24.70987	2.314485
30	30	29.51913	3.769172
35	41	39.95639	7.527346
40	71	68.17814	19.35202
45	77	76.19809	19.7766
50	82	81.47261	18.9314
55	107	104.6796	15.94924
60	141	137.6985	25.84882
65	148	147.0636	26.31187
70	160	158.8241	23.04088
75	185	182.6206	17.87597
80	200	198.4202	19.61779
85	207	206.2201	18.80456
90	214	213.2928	12.05796
95	231
100	286

FDiecast Polynomium (Prognose)          Datacoint

Рисунок 1. Экспоненциальное сглаживание динамического ряда числа разжижения с полиномиальной линией тренда

Figure 1. Exponential smoothing of the dynamic series of the liquefaction number with a polynomial trend line

Обсуждение

Следует отметить, что удобство исследуемого метода применительно к наблюдению динамического ряда числа разжижения заключается в возможности прогнозирования нестационарного временного ряда, имеющего случайные изменения уровня и угла наклона. По мере удаления от текущего момента времени t «в прошлое»

вес соответствующего члена ряда быстро (экспоненциально) уменьшается и практически перестает оказывать какое-либо влияние на значение экспоненциальной средней, заменяющей наблюдаемое значение ряда y t , когда в сглаживании участвуют все данные, полученные к текущему моменту t .

Метод прогнозирования сглаживания учитывает эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ. Экспоненциальная средняя y t является примером асимметричной взвешенной скользящей средней, в которой учитывается степень старения данных: более «старая» информация с меньшим весом входит в формулу (12) для расчета сглаженного значения уровня ряда [14-20].

Заключение

Проведение экспоненциального сглаживания динамического ряда числа разжижения кукурузной крахмалистой смеси позволяет получить достоверный прогноз о динамике показателя объекта исследования в изучаемом интервале. Стандартные погрешности прогнозируемых значений числа разжижения кукурузной крахмалистой смеси при дозировке амилопектинового кукурузного крахмала в смеси от 0 до 35,0%

Исследования выполнялись с использованием оборудования ЦКП «Исследовательский центр пищевых и химических технологий» КубГТУ (CKP_3111), развитие которого поддерживается Министерством науки и высшего образования РФ (Соглашение № 075–15–2021–679).