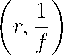Экстремальная задача Майлза-Шиа для мероморфных функций, определяемых модельной функцией роста

Одним из преимуществ метода изучения асимптотического поведения целых и мероморфных функций, основанного на ряде Фурье для In | f (re i ) | как функции от 6 , является то, что коэффициенты Фурье

Ck (r,f ) = г /2П e-™ ln |f (re* )| Ы, k G Z (1) 2n Jo выражаются через нули и полюсы мероморфной функции f и с их помощью можно изучать распределение нулей и полюсов [1]. Другое направление этой теории есть нахождение наилучших оценок сверху и снизу пределов отношений

N (r,f )+ N (r, 1/f) N (r,f )+ N (r, 1/f) N (r, 1/f) m 2 (r,f ) , T (r,f ) ’ m p (r,f )

в заданных классах мероморфных функций. Такие задачи называются экстремальными. В совместной работе Майлза и Шиа [2] была получена точная оценка снизу для первого из приведенных отношений. В настоящей работе мы распространяем некоторые результаты из [2] на классы мероморфных функций, определяемых модельной функцией роста. Доказываем следствие, относящееся к одной задаче Неванлинны, которая в общем случае до сих пор не решена.

1 Предварительные сведения

Мы считаем, что читатель знаком с основными сведениями из теории мероморфных функций [3] . В нашей работе будем использовать модельную функцию роста, введенную Б. Н. Хабибуллиным [4] (см. также [5] ). Нам понадобится лемма об асимптотическом поведении модельной функции роста, которая является следствием лемм 3 и 4 из [6] .

Лемма 1. Для X < p + 1

I (M(u)) ^p-X M 0 (u) du = r 0

для X > p +1

[ (M(u)) ^p-X M ⁰ (u) du = r

(M (r)) ^p+1-X

p +1 - X

(M (r)) ^p+1-A

X — p — 1

+ o((M(r)) ^{p+1 x} ) (r ^ m ) ,

+ o((M(r)) ^p+1-X )(r ^m ) . (2)

Определение 1. Пусть M — модельная функция роста. Мероморфная функция f называется функцией конечного порядка относительно модельной функции M, если

— In T (r,f ) ^lim

= p <  m .

r >^ ln M (r)

Класс данных мероморфных (целых) функций при фиксированной функции M обозначим через M ( E M ).

Нас будет интересовать случай, когда выполняется неравенство

M (2r) <  KM (r) ,r> 0,K >  0.

Заметим, что из условия (3) следует неравенство

-— In M(r)   In K r >^ ln r — ln 2 P

Нам понадобится лемма о пиках Пойя [7] .

Лемма 2. Пусть ψ 1 , ψ 2 , ψ — положительные непрерывные функции от r на луче [r o ; от ) такие, что отношение ^(r)/^ i (r) возрастает:

^^(r) i- ^^(r) n lim = от , lim = 0. r >^ ^ 1 (r) r >^ ^(r)

Тогда существует последовательность { r _n } , r _n → ∞ , если n → ∞ , такая, что при r = r n выполняется условие

№) <  ^(r) ^ 1 (t) “ ^ 1 (r)

r 0 <  t <  r ;

ictl <  ^ ^(r)  _r<  _t

^(t)   ^(r) ,

< ∞ .

Обозначим через C(0,R) = {z : | z | <  R} круг радиуса R> 0 с центром в начале координат. Коэффициенты Фурье мероморфной функции f в круге C(0,R) определяются формулой (1) . Справедлива следующая лемма [8, Lemma 13.4.1.].

Лемма 3. Пусть f — мероморфная функция в круге C (0, R), f (0) = 1, Z(f ) = { a _v } — нули, а W(f ) = {b ^ } — полюсы функции f,

∞∞ ln f(z) = X ak(f)zk = X ak zk k=1            k=1

— разложение в некоторой окрестности точки z = 0. Тогда для 0 < r < R справедливо co(r,f) = X ln Lrr- X ln rbi = NG?) - N(r,f);

|aν|≤r     aν     |bµ|≤r      µ ck (r, f)

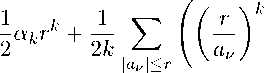
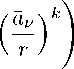
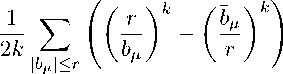
при k G N и C k (r, f ) = c - k (r, f ) при k G - N .

Будем пользоваться терминологией и определениями из [8] . Пусть µ — положительная мера в комплексной плоскости, конечная на каждом компакте и такая, что не нагружает некоторую окрестность нуля, то есть 0 i/ sup (ц) .

Определение 2. При k I N и r >  0 определим величины

S(r; к,ц)- к Z ^,

C(0,r)

S(r i ,r 2 ; к,ц) = S(r 2 ; к,ц) - S(r r , к,ц), r i <  r 2 .

Определение 3. Пусть M (r) — модельная функция роста. Положительная мера ц имеет конечную V(^-плотность, если существует положительная постоянная K такая, что r

N(r, ц):- j VQ _dt <  _Kv (r) r> o.            (6)

Положительная мера ц является мерой конечного V(r)-типа, если существует положительная постоянная K такая, что ц(г) < KV(r) .

Предложение 1 (Предложение 13.1.9. [8] ) . Если мера µ имеет конечную V (r)-плотность, то она является мерой конечного V (т)-типа.

Определение 4. Положительная мера ц называется V (r)-взвешенной, если существует последовательность комплексных чисел а = {а^ } £=i и положительная постоянная K, при которой для всех r >  0 и k I N выполняется неравенство

\а _к + S(r; к,ц)\ <

KV (r)_ rk   ’

и строго V(r)-взвешенной, если выполняется неравенство:

\а _к + S(r; к,ц)\ <

KV (r) kr ^{k .}

Пусть D = {an,qnY^=i — некоторый дивизор, т.е. множество комплексных чисел {an} вместе с их кратностями {qn}. По дивизору D определим меру ^D (G) = ^ qn- an ∈G

Определение 5. Дивизор D имеет конечную V(r)-плотность, если соответствующая ему мера ^ D имеет конечную V(r)-плотность.

Определение 6. Для k G N и меры ^ D обозначим

S 0 (r; k) = S 0 (r; к,

)=к#

C (0,r)

k d^D (Z ).

Определение 7. Пусть а = {ak}^1 — некоторая последовательность комплексных чисел. Функции co(r; ^d, а) = N(r, ^d); Ck(r; ^d, a) = 2{ak+S(r; k, ^d)} —|S(r; k, ^d), при k G N, и Ck = c-k при —k G N называются коэффициентами Фурье пары (^d, а).

Определение 8. Квадратичной полунормой пары (^d,а) называется m2(r; ^d,а)

^2 ^|c k ^(r ; ^ d ^,а)|2 . k = -^

Теорема 1. Пусть C k (r) = C k (r, ^ d , a) — коэффициенты Фурье пары (^ D ,a), a n = 0, для всех r >  0 удовлетворяющие условию

+м

X |^c k ^(r)| ² <  № .

k = -^

Тогда существует единственная целая функция f, f (0) = 1, для которой Z(f ) = D и C k (r, f ) = C k (r) для всех k G Z и всех r >  0 .

Это теорема 13.5.1 из [8] .

Замечание 1. Как следует из теоремы 13.4.5 [8] , если f G E m , то для ее дивизора нулей существует последовательность α такая, что выполняется соотношение (8) .

2 Мероморфные функции конечного порядка относительно модельной функции

Нам понадобится следующая лемма.

Лемма 4. Пусть f — мероморфная функция порядка ρ относительно модельной функции M, Z(f ) = {a _v } — нули функции f, W(f ) = {b ^ }, — ее полюсы. Тогда коэффициенты Фурье функции f при k > р равны

^C k ⁽r,^f ) = — 2k  X

| a ν | , | b µ |≤ r

+

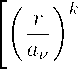
a ν

r

k

—

r

k

b

k

b µ

—

µ

r

Доказательство. Учитывая определения 2 и 6 , на основании леммы 3 имеем:

r k | a k (f ) + S(r,k,p z ) - S(r,k,p w ) |

< 2 | c k (r, f) + S'(r, k, p z ) - S(rr, k, p w ) | . (10)

Разделим последнее неравенство на M k (r) , где k > p , и перейдем в нем к пределу при r → ∞ . Используя неравенства [8 , Теорема 13.4.5] | C k (r, f ) |< AM ^p (r) и соотношения [8 , Предложение 13.2.2]

| S'rr,k,Z )

- S'{r,k,W) | =1 k

N (er, 1) + N (er,f )

находим, что правая часть неравенства (10) стремится к нулю. Тогда мы получим a k (f ) = -{ S( ro ; k,Z ) — S ( от ; k,W)},k > p . Подставляя эти значения a k (f ) в (5) , имеем (9) .

Основной результат статьи — следующая теорема.

Теорема 2. Пусть f — мероморфная функция порядка р, 0 < p < от, относительно модельной функции роста M, которая удовлетворяет условию (2). Тогда lim r→∞

N (r,f ) + N(r, f ) m 2 (r,f )

_> | sin ^пр | πρ

1 + sin(2np) /(2пр) ,

и это неравенство точное, т.е. для некоторой мероморфной функции f порядка ρ в (11) имеет место равенство.

Доказательство. Обозначим х = {x n } = {| a _v |} U {| b ^ |} , n(r) = n(r, f ) + n (r, 1/f ) , [p] = q ,

|a k (f ) | ,

Y k = <

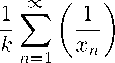
0 < k < q + 1, k>q + 1 .

Очевидно, что n(r,x) = n(r) . Достаточно рассмотреть случай q < p < q + 1, так как при целом p правая часть в (11) равна нулю и теорема тривиальна. Предположим, кроме того, что f (0) = 1 . Тогда при некоторых A >  0 , Е >  0 , p + Е < q + 1 справедливо неравенство

n(r) <   AM ^p+£ (r) для всех r >  0 . При k >  q +1 находим

k ck (r; x ) = - 2k L xn>r

c k ⁽ r; x,Y ) = ^- 2k

-

r

0 rk

xn≤r k∞ dn(t) + J ^-^ dn(t)

r

∞

n(t) ,     1

~dt + 2j

r

∞

r ) k n© dt tt

k

< A-  t d =

r

Arp+£

2(k - p - e). ( )

При оценке последнего неравенства мы использовали соотношения (4) +^

и (7). Таким образом, £ | Ck(r; x,Y) |2< ^. По теореме 1 существу-к=—ж ет единственная целая функция F, F(0) = 1, для которой х = Z(F) и Ck (r,F) = Ck(r; х, y) для всех r > 0 и всех k G Z. Используя соотношение (12) и интегрируя по частям, при k < q +1, находим

| C k (r,F )

| = ^{k 1} 2

r

k

dt

+

∞

r\ ^k N(t)

t

dt

-

N ( r ) ,

r

а при q = 0 и 1 <  k <  q имеем

1 k

⁰<  c k ^(r,F ) = 2 Y k ^r + 2

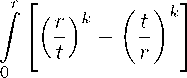
Nt) di + N (r).

Кроме того, | C k (r, f ) |< C k (r, F ) , 0 <  k <  q , так как при | a |> 1 и |c k (r,f ) | <  -C k (r,F ) , k >  q + 1 откуда

a -

| a |-

| a |

m 2 (r, f) <  m 2 (r, F ) •

Очевидно, что порядок функции N(r) не превышает p. На самом деле она имеет порядок ρ, так как в противном случае из теоремы Адамара [3, Теорема 4.1] следовало бы, что порядок функции T(r, f) — целое число, а этот случай мы исключили. По лемме о пиках Пойя для любого е > 0 существует последовательность {tn}, tn ^ от такая, что

N(t) <          N(tn),  0

N(t)< (fГ N(tn), tn< t< от. (16)

t_n

Последнее неравенство получается, если в лемме 2 взять

^(r) = N(r),   ^i(r) = r^{p £},   ^₂(r) = r^p+£.

Используя неравенства (16), из (13) и (14), получаем

| Ck(tn,F) |< N(tn)( k           - 1} , k > q +1,

[ (k — е)² — p²     J

| Ck(tn,F) |< N(tn) (7----У---ТГ2 + 1) + ¹Yktk,   1 < k< q.

L (p — е)² — k²J 2

Заметим, что из неравенства (16) вытекает, в частности, tn = o(N(tn)) при n ^ от, ибо при t0 таких, что rg < t' и N(tr) > (t')p-£, и для всех tn ≥ t0 выполняется tq+s < tP-£ < tP-£ Nt)- < n(tn), n n — n (t')p—€ — v nn если 2е < p — q.

Учитывая это замечание и произвольность ε, находим

T ¹ck\t_n, f) \ 2i I 2 2 11,™ ^llm --v™ .— < P ¹k^—P^{|,k 6}N.

п^ъ N (tn)

Используя равенство Парсеваля

{m2(r,F)}2 = X | ck(r,F) |2 = N2(r) + 2 X | Ck(r,F) |2, k=-^k=1

приходим к неравенству m2,F) JX    p4

Лъ N(r) < (k^ (P2 — k2)2/ '

Сумму ряда из правой части этого неравенства нетрудно найти с по- мощью вычетов. Она составляет

+ъ X k=-^

p⁴       1 / np \² / sln2np

.

(p²— k²)²   2 \sinp-p) \ + 2np

Так как N(r) = N(r, f) + N

, то из (15) и (17) получаем (11),

если учесть только что найденное выражение для суммы ряда.

Пусть f — целая функция с положительными нулями, ρ — нецелое,

N t,f j^ = -M^p(t) + o(M^p(t)),t ^ от, ak = 0, k = 1, 2,..., q = [p].

Тогда Ck(r, F) = Ck(r, f) для всех k G Z и всех p > 0. Находя асимптотику для Ck(r, f) с помощью соотношений (13) и (14), получаем lim r→∞

m2(r,f)

N (r, 1/f)

2∞

=1+2 X k=1

ρ⁴

(p²- k²)^2,

или

_r N (r, 1/f) _ | sin np If          2          1 ²

lim r >^ m2(r, f)       np       + sin2np/(2np) J т.е. оценка (11) точна. Если ρ — натуральное число, то эта оценка достигается для функции f (z) = exp(zp).

Теорема полностью доказана.

Приведем теперь следствие, относящееся к одной не решенной в общем случае проблеме Неванлинны, состоящей в нахождении точной оценки снизу величины

X(f) = lim r→∞

N(r, f) + N(r, 1/f) T (r,f)

Если f — целая функция, то 8(0, f) = 1 - x(f), где 8(0, f) — неванлинновский дефект функции f, т.е.

8(0, f)

^{m(r, 1/f}) r^ T (r,f) .

Приведенная ниже оценка значения x(f) является наилучшей из общеизвестных в настоящее время в классическом случае M (r) = r. Мы получаем такую оценку в случае достаточно общей функции роста M, удовлетворяющей условию (3).

Предложение 2. Пусть f — мероморфная функция порядка ρ, 1 < p < от, относительно модельной функции M. Тогда

X(f) > 0,9       ■.' .

p+1

Доказательство. Учитывая монотонность mq (r,f ) = (          | In |f (re1 ^)||q de\

12n 0o                      J по q и первую основную теорему теории распределения значений при f (0) = 1, имеем m2(r, f) > mi(r, f) = 2T(r, f) - N(r, f) - N (r, |

Таким образом,

X^(f)    —

-----— = lim

^{2 -}X^(f) ^rx

N (r, f) + N (r, 1/f)

.      N(r, f) + N(r, 1/f)

>lim -----------------

2T(r,f) - N(r,f) - N(r, 1/f)   r^      m2(r,f)

.

Используя (11) и неравенство

( sin 2пр 1 ²

[ + 2np J

- ^{1 +} 4Пр’

находим

2x/2

|sin 2np|

X^(f) >

ⁿP t ^{1 +} Л \   4np

1 +V2

|sin np|

)

ⁿP\¹ ' 1—

\   4np

|sin np|

^Пр ++ ¹ |sin np| 2^2   8^2   2 ¹

.

Поскольку n 10

2^2 < 9 , приходим к (18).

8^2 ⁺2

^{|sin n}P| < ¹⁰, 9

Заключение

Условие (3) на функцию роста M встречается в работах многих математиков, например в работах А. В. Абанина, испанского математика Ж. Бонета. В частности, в серии работ А. А. Кондратюка, опубликованных в Математическом сборнике в 80-х годах прошлого столетия, это условие играет ключевую роль при построении теории мероморфных функций вполне регулярного роста. В нашей работе условие (3) также используется при доказательстве основной теоремы.

Автор выражает признательность профессору К. Г. Малютину за постановку задачи и замечания, высказанные в процессе работы над статьей. Автор также выражает признательность рецензенту, замечания которого существенно улучшили содержание статьи.