Электрическая модель заряженной аэрозольной частицы в переменном электромагнитном поле
Автор: Билетов М.В., Михайлов В.В., Кузнецов И.Е.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 3 т.9, 2016 года.
Бесплатный доступ
В статье предложена модель токовой цепи заряженной аэрозольной частицы, позволяющая исследовать резонансные явления, возникающие в переменном электромагнитном поле.
Заряженные аэрозольные частицы, переменное электромагнитное поле, поверхностная проводимость частицы
Короткий адрес: https://sciup.org/146115070
IDR: 146115070 | УДК: 551.508.8 | DOI: 10.17516/1999-494X-2016-9-3-360-365
Текст научной статьи Электрическая модель заряженной аэрозольной частицы в переменном электромагнитном поле
При решении ряда важных практических задач используют допущения о том, что аэрозольные частицы, находящиеся в атмосфере, не имеют поверхностного заряда. Однако в природе довольно часто наблюдаются ситуации накопления большого количества заряда на части
Поэтому моделирование явлений, возникающих в заряженных аэрозольных частицах, находящихся под воздействием переменной электромагнитной волны, признано важной и актуальной задачей.
Цель данной работы – повышение качества информации о свойствах заряженных аэрозольных частиц, находящихся в переменном электромагнитном поле, путем построения модели токовой цепи и изучения на её основе резонансных свойств исследуемых аэрозолей.
Решение поставленной задачи осуществимо с помощью анализа первого уравнения Максвелла [2]. Под воздействием электромагнитной волны с напряженностью электрического поля Ė согласно уравнению Максвелла в заряженной аэрозольной частице возникают электрические токи, плотность которых можно выразить формулой jпол jсм jпров
Е • •
jпов gпров Е gпов Е ,
0t где jсм – плотность тока смещения; jпров – плотность тока проводимости аэрозольной частицы в отсутствие на ней заряда; j – плотность поверхностного тока; ε – диэлектрическая прони-пов цаемость вещества частицы, ε0– диэлектрическая постоянная, 8,85 10 ; gпров – удельная
м проводимость вещества частицы; gпов – удельная поверхностная проводимость частицы, обусловленная поверхностным свободным зарядом.
Полагая Е = Еm ejt, где w - круговая частота, t - время, будем иметь jпол
. ■ ■ ■
= Е-v д Е-v д Е. g см g пров g пов ,
где g^CM = j8о^со - комплексное отображение проводимости смещения.
В силу малости собственной проводимости аэрозольных частиц gп ов, обусловленной свой-пров ствами вещества, током проводимости можно пренебречь, тогда
jпол
= 5 Е+ я Е. см пов
Величину поверхностной проводимости gпов найдем из соотношения jпов
= g E = —V, g пов ,
2 r
где σ – поверхностная плотность заряда q аэрозольной частицы, имеющей радиус r; V – ско- рость движения заряда.
Таким образом,
V
g пов" 2 r-" Е ’
В переменном электрическом поле высокой частоты ω свободные электроны, находящиеся на поверхности частицы, будут двигаться со скоростью V под действием электрической силы (ионы не будут успевать перемещаться ввиду их большой массы).
F eFm cos t .
При этом уравнение движения с учетом столкновений электронов будет иметь вид [3]
еЕ m е i t m d d V t mV .
Решение этого уравнения представляет собой
V J-Veme-^ to + р to + р
• E, (8)
где e – элементарный заряд электрона; m – масса электрона; β – частота соударения электронов.
Таким образом, поверхностная проводимость частицы, обусловленная наличием на ней свободных зарядов, по аналогии с [4] будет определяться выражением
ст г em в - . emto 2rr L®2 + в to + в
Данная величина является комплексной и соответствует индуктивному характеру проводимости. C учетом (4) плотность поверхностного тока будет иметь вид ст Г (e/mв - i (e/mto 2п v.2 + в2 ®2 + в1
|
=1 |
Г ст ( e/m ) в " _ 2 n r to 2 + р 2 _ |
2 + |
Г ст ^ 1 _ 2 n r to 2 + в _ |
2 ,ю iarctg • Е 0 e рelto |
где

• E
m
ст_ Ыв ГГ ст Wto 2nr to + в I I 2nr to + в
– комплексная амплитуда поверхностного тока.
Анализ формулы (10) позволяет заключить, что поверхностное сопротивление частицы таково:
Z пов
1 2 n r(1 + в / ^ ) Г ^ 2 • 1 n
— =----^--7- — + i to = R,
& g пов
a (ejm)
L в
’ + itoL , пов пов
„ 2n r ( to 2 + в 2 )
гДе R noe =---- / / Afl
– омическое сопротивление (сопротивление потерь), обусловленное
T 2nr (1 + в2 Io 2)
переходом электромагнитной энергии волны в тепловую энергию; ьпов =------------- ин-
^ ( e/m )
дуктивность поверхности заряженной аэрозольной частицы, обусловленная отставанием (опережением) поверхностного тока от тангенциальной отставляющей напряженности электрического поля электромагнитной волны в зависимости от соотношения частоты резонанса и частоты воздействующего электромагнитного поля.
Представим плотность тока смещения в виде i e
J c = i e 0(1 + X ) m E = i e o em E,
где χ – поляризуемость аэрозольной частицы.
Анализ размерностей в формуле (12) позволяет сделать вывод о том, что проводимость, обусловленная процессами смещения, имеет емкостную природу.
Для определения полного тока, протекающего в заряженной аэрозольной частице, необходимо воспользоваться интегральным уравнением Максвелла:
I = J jdS = J jCM dS + J j „ os dS . SS S
Для сферической частицы решение уравнения (13) будет иметь вид
I = J jdS = J teem E dS +J—[em^-S S 0 S П Lm2 + в
. 2
- i
em m 1. e ds . ® 2 + в 2 j
В полярной системе координат с учетом тангенциальной составляющей напряженности электромагнитного поля, обусловливающей поверхностный ток, получим:
— r
I = teemn • r E + 02
^^^^^^^B . Jemjm m2 + в2 E.
При определенных сочетаниях размеров аэрозольных частиц, их зарядов, а также диэлектрических
свойств
согласно представленной модели будет наблюдаться резонанс токов. Поэтому заряженную аэрозольную частицу, находящуюся в переменном электромагнитном поле, можно представить в виде эквивалентной схемы токовой цепи (рис. 1).
Анализ рис. 1 показывает, что заряженная аэрозольная частица, находящаяся под воздействием переменного электромагнитного поля, представляет собой параллельный колебательный контур, характеристиками которого является собственная резонансная частота и0 и добротность
Q
:
®
0
a
(e/m)
2mss0(1 + в/®2)
,
Q
=
^
o
L
R
®
o
'
2
n
r(1
+
в/®2
)
a
(e)m)
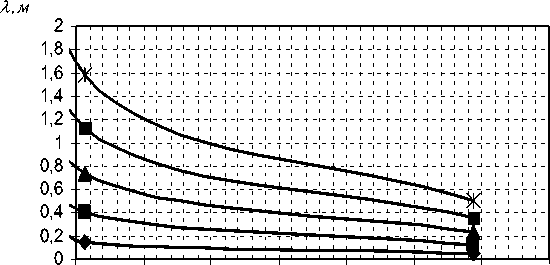
R Расчеты, проведенные с использованием предлагаемой модели, представлены на рис. 2. Рис. 1
1E-09 3E-09 5E-09 7E-09 9E-09 1,1E-08 1,3E-08
σ
,Кл/м2
Ряд1 Ряд2 Ряд3 Ряд4 Ряд5 Рис. 2 Анализ модели и результатов расчетов позволяют сделать следующие выводы:
1. При определенных соотношениях размеров аэрозольных частиц, поверхностной плотности их заряда, а также частоты воздействующей электромагнитной волны возникают резонансные явления.
2. Значение частоты, на которой происходит резонанс, зависит от электрофизических свойств аэрозольной частицы и величины её заряда.
3. Резонансные явления наблюдаются в дециметровом и метровом диапазоне длин волн для частиц радиусом от 10 до 50 мкм, имеющих заряды от
1.6 • 10-19 Кл
до
1.6 • 10-16 Кл.
Результаты исследований подтверждаются экспериментами с дисперсными системами [5–8]. Таким образом, построенная электрическая модель токовой цепи заряженной аэрозольной частицы в переменном электромагнитном поле может служить основой для получения информации о зарядах аэрозольных частиц облачности и осадков радиолокационным методом.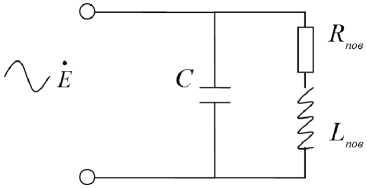
Список литературы Электрическая модель заряженной аэрозольной частицы в переменном электромагнитном поле
- Ельцов В.А. К вопросу о влиянии поверхностного заряда диэлектрических сфер на рассеяние электромагнитных волн. Тр. САРНИГМИ. 1977. Вып. 48(129). С. 88.
- Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука, 1989. 285 с.
- Долуханов М.П. Распространение радиоволн. М.: Сов. радио, 1960. 273 c.
- Boheren C.F, Hunt A.J. Scattering of electromagnetic waves by a charged sphere. Can. J. Phys., 1977. Vol. 55. P. 1930.
- Духин С.С. Электропроводность и электрокинетические свойства дисперсных систем. Киев, Изд-во «Наукова Думка», 1975. 256 c.
- Кузнецов И.Е., Билетов М.В. Сверхкраткосрочный прогноз опасных явлений погоды по радиолокационным данным с учетом энергетического состояния атмосферы. Наукоемкие технологии. 2012. Т. 13, № 3. С. 21 -26.
- Патент РФ 2319981 (2008)//Б. И. 2008. № 8.
- Патент РФ 2491574 (2013)//Б. И. 2013. № 24.


