Электрофлуктуационный метод оценки качества биполярных транзисторных структур

Ульяновское отделение Института радиотехники и электроники РАН

Обсуждаются задачи, относящиеся к применению параметров и характеристик НЧ шума для оценки качества транзисторных структур. Предложена физическая эквивалентная шумовая схема транзисторной структуры, учитывающая неоднородность токораспределения по площади эмиттерного перехода и влияние распределенных сопротивлений активных областей. Обсуждается возможность использования предложенной схемы для анализа экспериментальных результатов и обоснованного выбора режимов и условий измерения НЧ шума в задачах диагностики транзисторных структур. Результаты теоретического анализа подтверждаются экспериментом.

Возможность применения параметров и характеристик электрических флуктуаций тока (напряжения) со спектром типа 1/f, возникающих в изделиях электронной техники (ИЭТ) для оценки их качества и прогнозирования физической надежности изучается в течение многих лет [1-5]. В литературе этот тип флуктуаций часто называют фликкер-шумом, избыточным шумом, низкочастотным шумом (НЧ шум). В целях краткости будем пользоваться в дальнейшем названием НЧ шум. Интерес к указанному типу флуктуаций обусловлен тем, что уровень НЧ шума и другие его характеристики в сильной степени зависят от концентрации неконтролируемых дефектов, возникающих как на поверхности, так и в объеме ИЭТ (загрязнения, нарушения целостности защитного окисла, микротрещины, дислокации, несовершенство контактов и т.п.), то есть НЧ шум должен обладать высокой информативностью в задачах диагностики ИЭТ. В этом направлении получен ряд положительных результатов. Так можно считать твердо установленным: ИЭТ, уровень шума которых на три - четыре порядка превышает среднестатистическое значение для генеральной совокупности, имеют крайне низкую надежность; изделия, уровень НЧ шума которых растет в процессе испытаний, отказывают на ранней стадии работы изделия [4]. Вместе с тем, хорошо известны случаи, когда ИЭТ, имевшие низкий уровень НЧ шума, отказывали в процессе испытаний раньше «шумящих»; с другой стороны, отнесенные по уровню НЧ шума к потенциально ненадежным - при испытаниях не отказывали. Причина такого несоответствия, имеющего место при использовании параметров НЧ шума в качестве информативных в задачах диагностики ИЭТ, остается невыясненной до сих пор. В [3] отмечается, что для получения достоверной оценки качества транзисторов по результатам измерения НЧ шума необходимо тщательно обосновывать режим его измерения. Известно, что параметры и характеристики НЧ шума зависят от протекающего через изделие тока, приложенного напряжения, сопротивления источника сигнала (в случае транзисторной структуры) и внутренних физических параметров ИЭТ. Не учет этих факторов может дать любой результат, в том числе и противоположный ожидаемому.

В настоящей работе ставится задача выяснения условий и режимов измерения параметров НЧ шума, при которых обеспечивается наиболее высокая достоверность выявления потенциально ненадежных биполярных транзисторных структур. Анализ проведен методами теории шумящих четырехполюсников и физических шумовых эквивалентных схем.

Из теории шумящих четырехполюсников известно, что исследуемый транзистор можно представить нешумящим с вынесенными двумя генераторами шумов, между которыми, в общем случае, может быть статистическая

Рис. 1. Физическая шумовая эквивалентная схема биполярной транзисторной структуры

связь [3]. Обычно электрические шумы приводятся ко входу исследуемого прибора. В этом случае шумовыми параметрами являются: генератор шумовой ЭДС ^^2, включенный последовательно со входом, генератор шумового тока 2 , шунтирующий вход, и коэффициент корреляции между ними.

Генераторы шумовой ЭДС и шумового тока вычислим с помощью физической шумовой эквивалентной схемы биполярной транзисторной структуры, показанной на рис.1.

При составлении указанной схемы учитывались следующие основные особенности транзисторной структуры. Здесь в рассмот рение приняты только источники электрических флуктуаций со спектром типа 1/f и локализованные в областях эмиттерного и коллекторного переходов. С учетом этого введены сопротивление пассивной и активной области эмиттерного перехода, соответственно; а! , а-1эа - токи коллектора пассивной и активной областей, соответственно, где а- коэффициент передачи по току; ^Л = кп ,

2а = ка - шумы утечки пассивной и активной областей коллекторного перехода, соответственно; гкп , гка - дифференциальное сопротивление пассивной и активной областей коллекторного перехода, соответственно; Rh - сопротивление нагрузки. Анализ проведен при следующих допущениях: шум пере дается со входа транзистора на выход только через эквивалентные генераторы тока а-1эп и а-1эа; все сопротивления активные, что достаточно хорошо выполняется в области низких частот; коэффициент передачи по току аа от частоты не зависит; сопротивления кол лекторного перехода гкп , гка велики, т.е.

источники шума: , 2 =   - тепловые шумы

V Rr Rr

^г кп , ^г ка >> ^г бп , ^г ба

г эп

гэа .

сопротивления генератора Rr;

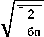
бп

В соответствии с принципом суперпо

зиции, флуктуационный ток в нагрузке будет

тепловые шумы сопротивления пассивной базы г, ; J 2 =   - тепловые шумы сопро- бп “ у ба ба                                    к тивления активной базы г, ; J 2 = - низ-ба эп эп кочастотные шумы пассивной области эмиттерного p-n перехода; ^2" = - низкочастотные шумы активной области эмиттерного p-n перехода; гэп , гэа - дифференциальное представлять сумму токов от всех источников. Нас в дальнейшем будут интересовать наиболее важные в рассматриваемом случае составляющие шумового тока, обусловлен ные источниками эп, . На исследование этих составляющих мы в дальнейшем и ориентируемся. Расчет по приведенной эквивалентной схеме дает следующие выражения для составляющих шумового тока в нагрузке.

Т2 ₌   ф + 1) 2 - R 2 - i^

¹     [R i + ф +1) - Г эп ] ²

eг

Г ^1 Тдд^ч^+ l в )  [ rt. + rt. + (в +1)-Гз ]2   •

а где р - -    - коэффициент передачи по

1-а току в схеме с общим эмиттером;

+г ^1 1

l в )

^Г, ^{2 - [ Г}^ ⁺ Г з. ^{- ( в + 1)]2} rr i

[ ^Г,. ⁺ r,. ⁺ ( ^{в +} 1) ^{- Г} з ]^{2    3€}

i 2

- (- + ) . г V ба эа 7

^бп + б + г ба эа

,

(в+1) ² - R 2 - £

[R 2 + ф + 1) - Г эа ] ²

где э ^— эп ⁺ эа = ¹

э

эп

+

эа

где

- (- + )

__            г V бп эп 7

^{2 ба} + _й + г бп эп

•

Эквивалентный шумовой ток определим из соотношения

Тогда

Н Х.Х.                                    г-»

" 2    , где    i х.х. =Р i х.х.

Суммируя (1) и (2), получим выражение для шумового токавнагрузке:       _ ч — (Р+1)2 - R2 -12. + (в+1)2-R 2 - г " [R1 + (Р +1)- г„]2 [R2 + (в +1) - г,]2 (3)

При коротком замыкании по входу, т.е.

R = 0:

— _— н ■ 1, - r - ,      ₊ ' e + 1, - r - ,

’        [Г бп + ( в + 1) - Г э_п ] ²     [Г ба + ф + 1) - Г эа ] ^{2 (4)}

При разомкнутом входе, т.е. г - ^

2 —Г в ±1 1

l в +Г в ±- 1 ²

l в )

⁽ rf ^{+ Г},. ^{+ г} з€ ⁾² i² з ²

)

^[ r,. + rf. + ^г з€ ^{+ ( в + 1) - г} з^ ^]2

⁽ rf ⁺ r,. ^{+ г} з^ ^{)2 - 2} з€

^{[ Г},. ⁺ , ^{+ г} з^ ^{+ ( в + 1) - г} з€ ^]2

+

i У _— ^{( в + 1)2 -} ( rf ⁺ rf ^{+ Г} з€ )^{2 - 2} з² +

¹ ' '"     ^[ rf ^{+ Г} ,- ^{+ Г} з€ ^{+ ( в +} 1) ^{- Г} з. ^{] 2}

+ ^{( в + 1)2 - (} rf ⁺ rf ^{+ Г} з- ^{)2 - 2} 2€       ’ ⁽⁵⁾

^{[ Г},. + f,. + r₃. + ⁽ Р + 1) ^- r ₃€ ]²

Среднеквадратическое значение напряжения шума 0 , приведенное к входу исследуемого транзистора при C = 0 определим из хорошо известного соотношения [3] _{= +} ^.--²₊           (10)

ш           1          г 1 Rг              V 7

где R _— 4 _{- - - г -} А - тепловой шум сопротивления генератора.

Учитывая (7), (9) и (10), окончательно получим

Эквивалентную шумовую ЭДС ² опре

делим как

U ²

где

u к.з.

_    2      2

2 __ н к.з. н

^—     2

u к.з.

г в + 1 ] ’

^{1 в} 7

Г 2 . ^{- [} Г ,. ⁺ Г з€ ^{- ( в + 1)]2} +

^{[ Г} ,. ^{+ Г} ,. ^{+ ( в + 1) - Г} з ^]2

₊      ^{( Г} ,. ^{+ Г} ,. ^{+ Г} з€ ^{)2 -} R <

^{[ Г} ,. ^{+ Г} ,. ^{+ Г} з€ ^{+ ( в + 1) - Г} з^ ^]2

L 2 з ² +

- коэффициент усиле

Г в + ¹ 1 ²

ния по напряжению при коротком замыкании по входу;

_— [ бп + эп - (Р + 1)] - [ + эа - (Р + 1)]

^вХ           бп ⁺ ба ^{+ (} эп ⁺ эа ) ^{- ( в +} 1)       '

l в )

^Г, ^{2 - [ Г},. ⁺ Г з. ^{- ( в + 1)] 2} ₊

[ Г ,. + Г ,. + ( в + 1) - Г з ] ²

+       ( ^Г,. ^{+ Г},. ⁺ Г з. ^{) 2 - R}<²

^{[ Г},. ^{+ Г},. ⁺ Г з. ^{+ ( в + 1) -} Г з€ ^{] 2}

Тогда (6) окончательно запишется в виде

+ 4-k-T-Rr-Af            (11)

Выражение (11) показывает, что среднеквадратичное значение шумового напряже-

ния сложным образом зависит от внутренних физических параметров транзистора, в том числе и от электрического режима его работы. В целях удобства дальнейшего анализа введем следующие обозначения:

б 2 п " [ ба ⁺ эа " ^{( в +} 1)] 2

^[ бп ⁺ ба ⁺ э " ^{( в + 1 )]} 2 ’

б ² " ^[ бп ⁺ эп " ^{( в + 1 )]} 2

^[ бп ⁺ ба ⁺ э " ^{( в + 1 )]} 2 ’

где к- коэффициент, зависящий от состояния поверхности и объема структуры и характеризующийся сильным разбросом от прибора к прибору’ 1к - ток коллектора (1к = аА’ n, m - коэффициенты, величина которых не превышает 2 (теоретическое значение 2)’ f -частота’ Af - эквивалентная шумовая полоса частот, в которой производится измерение шума.

С учетом (11), (13) выражение (12) примет следующий вид:

(А + + ) ²

__________ V бп _____ ба _____ эа / ____________

[ +   + + ■ (В +1)]2 ’ бп ба эа эп

9        1

U² = ( A + C ■ R 0) ■ k ■       +

^ ^{v          <} / • в 2 f

(А + « + ) 2

__ ___________ V бп ______ ба ______ эп ' _____________

= [ „ + + + ■ (В +1)] 2 • бп ба эп эа

Тогда (11) примет более простой для ана лиза вид:

+ ( B + D ■ R 0 ) ■ k.

I l_e ■A f в ² ■ f

ш

= ( +

² ) ■ ² + ( + г эп

■

² ) ■ ²

г эа (12)

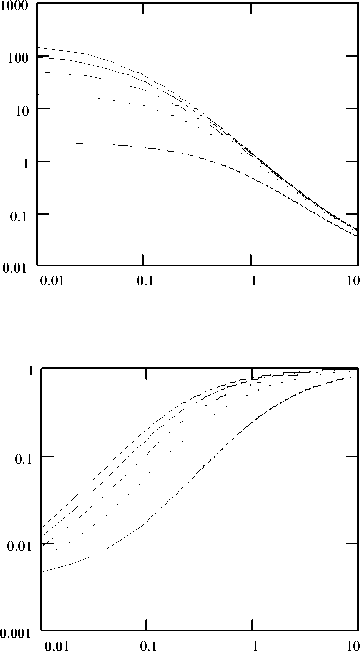
На рис. 2 показаны зависимости коэффициентов а, в, с и d стирка эмдаерчтри рб^ЧМучМоэДО A, в, с и D являются функцией 1_э, г_бп , г_ба, в и эта зависимость в широком диапазоне токов является нелинейной. Наибольшее изменение по аб

солютному значению при изменении гбп испытывает коэффициент A и, как следствие, составляющая НЧ шума от генератора шумо

вого тока ² . Зависимость коэффициента В от г_бп проявляется только в области достаточно больших токов эмиттера. Сопротивление г_ба влияет в сильной степени на все коэффициенты, входящие в (12). Отсюда следует вывод о том, что экспериментально измеренный и приведенный ко входу исследуемого транзистора шум и его зависимость от электрического режима сложным образом зависит как от внутренних, определенных технологией изготовления физических параметров (г_бп, г_ба, в, 0 ), так и внешних, поддающихся управлению параметров (R, 1_э). Входящие в выражение (12) генераторы шумового тока 2 _п, 2 _а в общем случае имеют вид [1, 2, 3 ]:

ш

n ■А em ■

,

где кп, ка - коэффициенты, характеризующие состояние поверхности и объема, соответственно’ I , 1эа - приповерхностная и объемная составляющие тока эмиттера, учитывающие неравномерность распределения тока по площади эмиттерного перехода.

Следует отметить, что входящие в (14) коэффициенты кп и ка, а также токи I и I имеют существенно разные величины. Коэффициент кп на один и более порядков превышает ка, так как степень легирования приповерхностной области эмиттерного перехода значительно выше объемной, лежащей под эмиттером, и, как следствие, дефектность структуры в этих областях (неоднородности, дислокации и т.п.) оказывается также на один и более порядков выше объемной области. Различие в величине токов I и I обусловлено неравномерностью токораспределения из-за падения напряжения на активном сопротивлении базы и может достигать 30 % и более.

На рис.3, с учетом сделанных замечаний, показаны зависимости 2 от тока эмит-ш тера, построенные по (14) и измеренные экспериментально у транзистора типа 2Т908А на частоте 1 кГц. Видно, что в диапазоне изменения тока от 0.01 А до 0.2 А имеется хорошее согласие теоретических и экспериментальных кривых. В области токов от 0.2 А до 1.0 А заметно их расхождение. Причина слабой зависимости 2 от тока в диапазоне ш

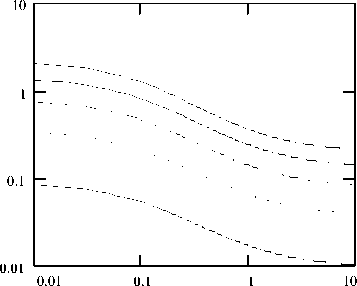
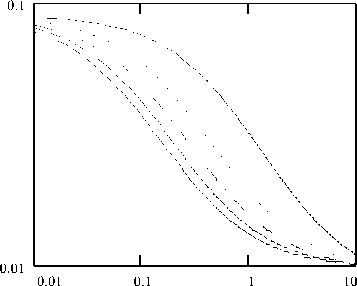
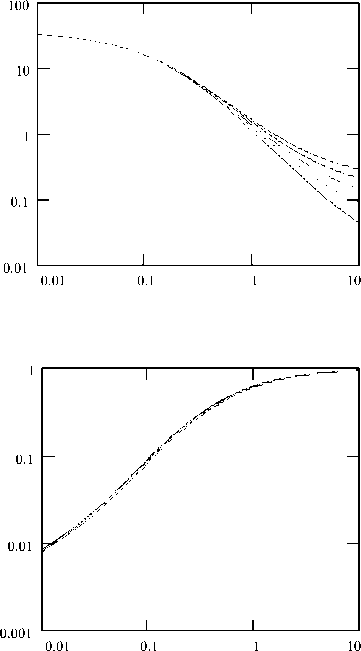
Рис. 2. Зависимости коэффициентов A, B, C и D от тока эмиттера при различных значениях гбп и гба: а), б), в) - гба=4 Ом, гбп=0.1...0.5 Ом; г), д), е) - гба=1...9 Ом, гбп=0.1 Ом

0.2^0.5 А, как выяснено в независимом эксперименте по исследованию температурных и токовых зависимостей прямого падения напряжения Иэб, обусловлена перераспределением тока по площади эмиттера и, в конечном счете, локализацией его в пределах малых областей. То есть из зависимости 2 от ш тока эмиттера имеется возможность получать информацию о степени однородности токо-распределения по площади эмиттера.

На рис.4 и рис.5 представлены теорети ческие и экспериментальные зависимости 2 от сопротивления источника сигнала R ш                                                         г при различных значениях гбпи 1э. Видно, что в этом случае имеются две области: 2 =const (для Rг<<1 Ом) и 0 =F( 2) (для Rr>10 Ом). Промежуточная область является переходной и зависит от величин гбп и 1э. Для решения нашей задачи диагностирования состояния структуры наибольший интерес представляет ход рассматриваемой зависимости 0 от

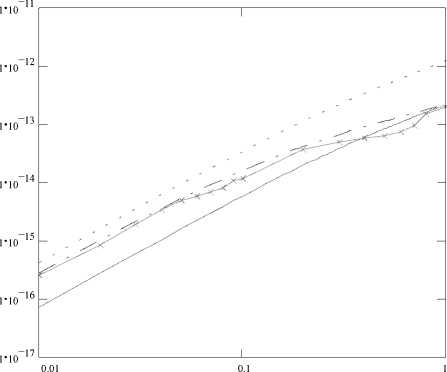
Рис. 3. Зависимость U 0 от тока эмиттера для различных значений г_6п и г _6д . 1- r=0.3 Ом, r₆=1 Ом; 2 - r_6n=0.1 Ом, г_6а=3 Ом; 3 - г_6п=0.1 Ом, г₆=1 Ом; 4 -данные эксперимента

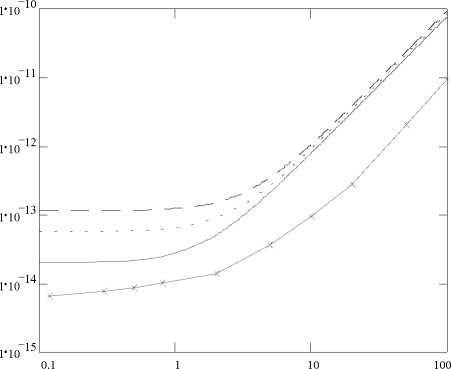
Рис.4. Зависимость U2 от сопротивления источника сигнала Нг при 1э=0.2 A, r =1 Ом и различных значениях г6п: 1 - г6п=0.3 Ом; 2 - г6п=0.2

Ом; 3 - г6п=0.1 Ом; 4 - данные эксперимента

г_бп. Из рис.4 видно, что с ростом г_бп переходный участок кривой смещается в область больших значений R_r. Отсюда можно сделать вывод о том, что зависимость 0 =F( 2 ) при I₃=const можно использовать для получения оценок величины г_бп. Из [8] известно, что г_бп повышает температурную стабильность транзистора при работе его в режиме больших токов.

В целях проверки изложенных соображений проведены испытания кремниевых мощных транзисторов на воздействие повышенных нагрузок. Исследовались транзисторы типа KT803A в количестве 50 штук. Испытания проводились при Ик= 30В, 1к=1.5 А, Тк = 120°С в течение 8час. Перед испытанием измерялись основные электрические параметры, а также шумовые параметры на частоте 1 кГц в режиме Ик=20В, 1к= 0.2 А, Rr равном 1 Ом и 2 Ом. За критерий качества был принят коэффициент KR, определяемый как отношение шумового напряжения, измеренного при Rr равном 2 Ом к шумовому напряжению, измеренному при Rr равном 1 Ом. Статистическая обработка результатов измерения по коэффициенту KR показала, что транзисторы по величине KR подчиняются распределению Пирсона. На рис.6 показана корреляционная связь между величиной коэффициента KR и процентом отказов транзисторов, сгруппированных в интервалы по вели чине этого коэффициента. Видно, что с ростом коэффициента KR , что соответствует уменьшению гбп , надежность транзисторов снижается. То есть коэффициент KR можно использовать в качестве информативного параметра при оценке качества транзисторных структур на основе шумовых измерений.

На основе проведенных исследований и данных других авторов можно сделать следующие выводы о возможности использования параметров и характеристик НЧ шума в задачах диагностики транзисторных структур:

• 1)    Уровень НЧ шума, измеренный у реальных транзисторов и превышающий по величине на три, четыре порядка среднеста-

• Рис.5. Зависимость U2 от сопротивления источника сигнала Нг при r =1 Ом, г6п=0.1 Ом и различных значениях 1э:

1 - 1э=5 A; 2 - 1э=1 A; 3 - 1э = 0.1 A; 4 - 1э = 3 A (данные эксперимента);

5 - 1э = 0.2 A (данные эксперимента)

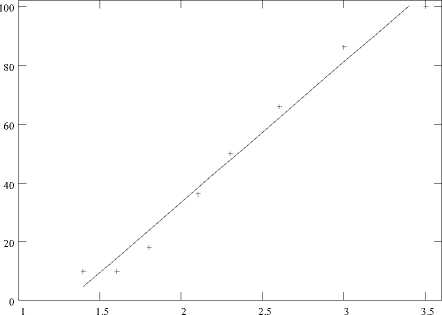
Рис. 6. Корреляционная связь между величиной коэффициента КК и процентом отказов транзисторов, сгруппированных в интервалы по величине этого коэффициента тистическое значение, свидетельствует о крайне низкой надежности транзисторной структуры;

• 2)    Уравнение (14), полученное на основе анализа предложенной физической шумовой эквивалентной схемы, достаточно хорошо описывает зависимость шумовых параметров и характеристик от физических параметров транзисторной структуры и режима ее работы и позволяет методом последовательных приближений получать оценки таких важнейших параметров как г_бп и г_ба;

• 3)    По аномальным участкам в зависимости 0 =Р(1_э) представляется возможность выявления транзисторных структур с локализацией тока и получения оценок величин этих токов;

• 4)    Температурную стабильность транзисторных структур можно оценивать по вели

чине коэффициента KR, равного отношению шумовых напряжений, измеренных при двух значениях Rr.