Электронно-энергетический спектр одноэлектронных состояний каркасных алициклических наноструктур с локальными дефектами замещения

Неэмпирическая процедура Хартри-Фока-Рутана в базисе STO-3G с учетом корреляции электронов по теории возмущений Меллера-Плесета второго порядка применена к расчету энергий одноэлектронных состояний наночастиц угле-, кремний- и германий-водородов (увеличение объема этих частиц приводит к структурам соответствующих тетраэдрических полупроводников). Обсуждены особенности спектра одноэлектронных состояний изучаемых наночастиц, обусловленные дефектами замещения центрального атома на атомы из третьей и пятой групп того же периода.

Молекулярные структуры нанометровых размеров (МСНР) привлекают внимание исследователей в связи с возможностью использования их в качестве поверхностных образований на различных твердотельных подложках, применяемых в нано- и микроэлектронной технике. Электронный энергетический спектр МСНР накладывается на спектр соответствующей поверхностной структуры, модифицируя его. Дефекты в объеме МСНР приводят к появлению дополнительных электронных состояний, локализация которых в спектре зависит от типа вводимого дефекта. МСНР на основе каркасных алициклических (КА) угле-, кремний- и герма-ний-водородов интересны тем, что с увеличением их объема они переходят в кластеры, а затем кристаллы полупроводниковых твердотельных соединений типа алмаза, кремния и германия соответственно.

В данной работе нами рассмотрены высокосимметричные С-, Si- и Ge-КА-водородные структуры (КАВС), в центре которых атом АЦ (C, Si или Ge), в тетраэдрическом окружении которого – атомы I координационной сферы (КС) (АI), которые в свою очередь окружены атомами II КС, а те – атомами III КС (АIII). Атомы АIII замыкались «снаружи» атомами водорода (VI КС) [1]. Такие КАВС имеют размер порядка 1 нм, их строение представлено на рисунке 1.

Путем дальнейшего «наращивания» числа КС нетрудно получить КАВС больших размеров. Число атомов в них быстро увеличивается (табл. 1). Для конкретных расчетов нами выбран нано-кластер с тремя сферами соседей, который содержит 41 атом основного элемента (С, Si или Ge) и 60 атомов водорода (рис. 1). Нанокластеры больших размеров нами не рассматривались из-за существенно возрастающих вычислительных трудностей, возникающих ввиду необходимости включения в систему большого числа атомов.

Длины связей в рассчитываемых структурах выбраны в соответствии с их средними значениями в родственных соединениях R(C-C) = 1,54 Å, R(Si-Si) = 2,22 Å, R(Ge-Ge) = 2,44 Å, R(C-H) = 1,09 Å, R(Si-H) = 1,43 Å, R(Ge-H) = 1,54 Å [2]. Нами изучены также высокосимметричные КАВС с дефек- том замещения центрального четырехвалентного атома А на атомы из того же периода, но относящихся к 3 и 5-й группам периодической системы: C → B, N; Si → Al, P; Ge → Ga, As.

Рис. 1. Модель МСНР, содержащей вокруг центрального атома три сферы соседей:

• 1    – атомы углерода, кремния или германия; 2 – атомы водорода

Таблица 1

Количество атомов основного элемента и атомов водорода и размеры угле-, кремний- и германий-водородных структур

Число КС	Число атомов А	Число атомов Н	Размер МНСР, нм
			С	Si	Ge
2	17	36	0,68	0,96	1,05
3	41	60	0,93	1,24	1,45
4	83	108	1,19	1,68	1,84
5	147	148	1,44	2,04	2,24
6	239	220	1,69	2,41	2,64
7	363	276	1,94	2,77	3,04
8	525	372	2,20	3,13	3,43
9	729	444	2,44	3,49	3,77
10	981	564	2,69	3,86	4,23

Расчеты выполнялись в рамках неэмпирической процедуры Хартри-Фока-Рутана [3] в базисе STO-3G [4]. Поправки к полным энергиям КАВС, обеспечивающие учет корреляции электронов, рассчитывались по теории возмущений Мёллера-Плессета второго порядка [5]. Полученные значения эффективных зарядов на атомах различных КС приведены в таблице 2, а рассчитанные диаграммы плотностей электронных состояний *) приведены на рисунках 2–4.

Как следует из таблицы 2, в бездефектных КАВС заряды на центральном атоме и атомах первой КС почти нулевые, то есть влияние на эти атомы со стороны концевых атомов водорода незначительно. Перераспределение зарядов имеет место преимущественно между атомами Н и атомами третьей КС. В структурах с дефектом замещения заряды на атомах-дефектах из 3-й группы – положительны (эти атомы отдают электронную плотность остатку КАВС), а на ато- мах-дефектах из 5-й группы – отрицательны (эти атомы стягивают на себя электронную плотность с остатка КАВС).

Таблица 2

Заряды на атомах q _m различных координационных сфер угле-, кремний-и германий-водородных структур (бездефектных и с локальными дефектами замещения)

№ координационной сферы			0	1	2	3	4
			q 0	q 1	q 2	q 3	q Н
С-КАВС	бездефектная структура		–0,01	0	0,04	(–0,20)–(-0,12)	(0,02)–(0,08)
	дефект замещения	B	0,17	–0,06	0,04	(–0,20)–(-0,11)	(0,02)–(0,08)
		N	–0,24	0,07	0,04	(–0,20)–(-0,12)	(0,02)–(0,08)
Si-КАВС	бездефектная структура		–0,02	–0,01	0,03	(0,30)–(0,40)	(–0,18)–(–0,13)
	дефект замещения	Al	0,31	–0,10	0,03	(0,30)–(0,41)	(–0,18)–(–0,13)
		P	–0,24	0,07	0,04	(0,30)–(0,40)	(–0,18)–(–0,13)
Ge-КАВС	бездефектная структура		–0,01	–0,01	0,01	(0,24)–(0,33)	(–0,14)–(–0,10)
	дефект замещения	Ga	0,17	–0,06	0,04	(0,24)–(0,33)	(–0,14)–(–0,10)
		As	–0,24	0,07	0,04	(0,24)–(0,33)	(–0,14)–(–0,10)

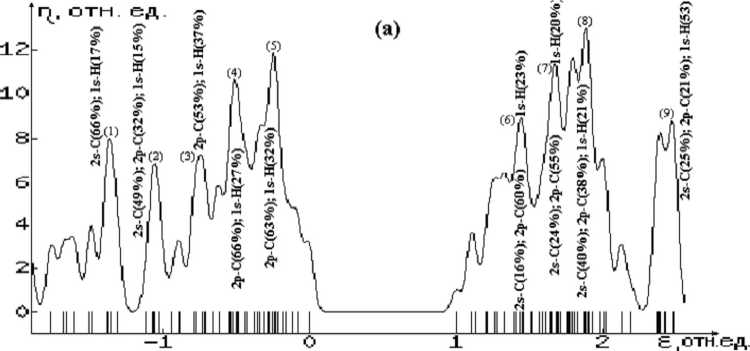
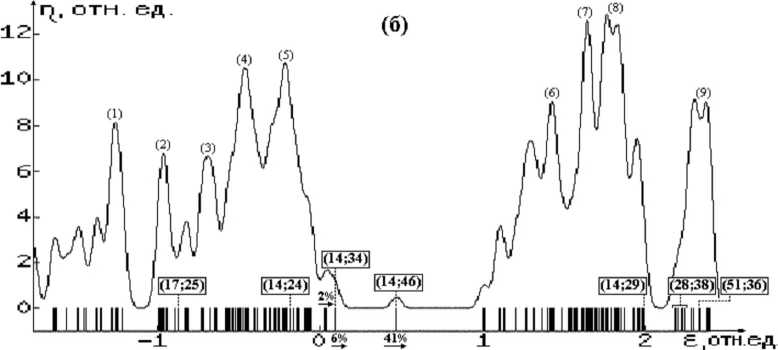
Рис. 2. Плотности электронных состояний угле-водородных МСНР:

• (а) – без дефекта; (б) , (в) – с дефектами замещения С(В) и С(N) соответственно

[в скобках указаны вклады (%) орбиталей атомов дефекта и атомов первой КС;

энергии отсчитываются от верхней границы ГЗС; за единицу энергии принята ширина ОЗС БС] (см. также окончание рисунка на следующей странице)

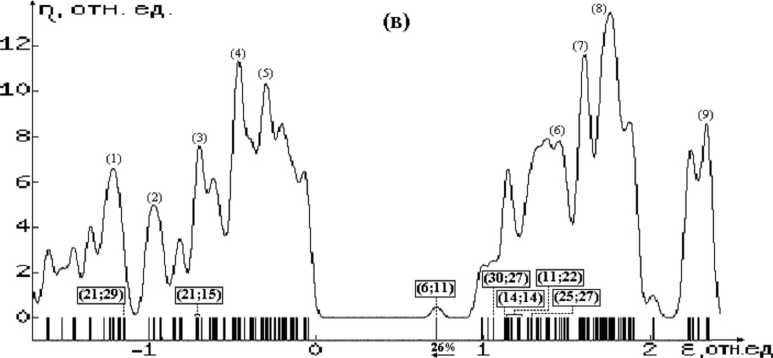
Рис. 2. Окончание

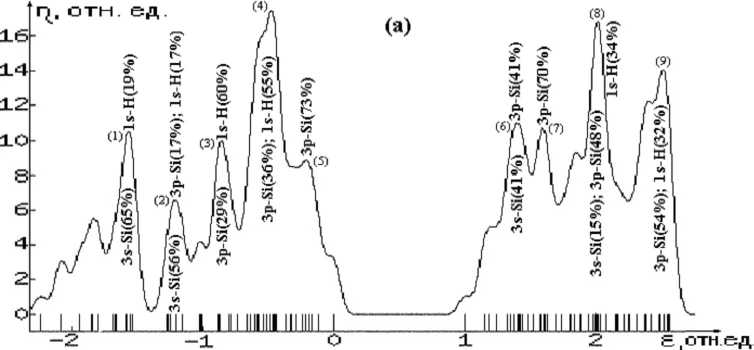
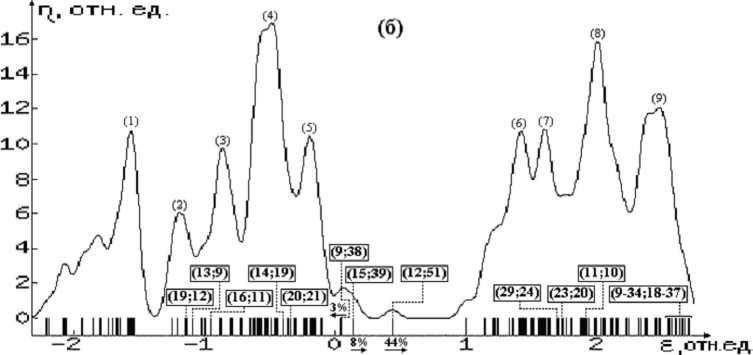
Рис. 3. Плотности электронных состояний *⁾ кремний-водородных МСНР: (а) – без дефекта; (б) , (в) – с дефектами замещения Si(Al) и Si(P) соответственно (см. также окончание рисунка на следующей странице)

*) Cм. пояснения к рисунку 2.

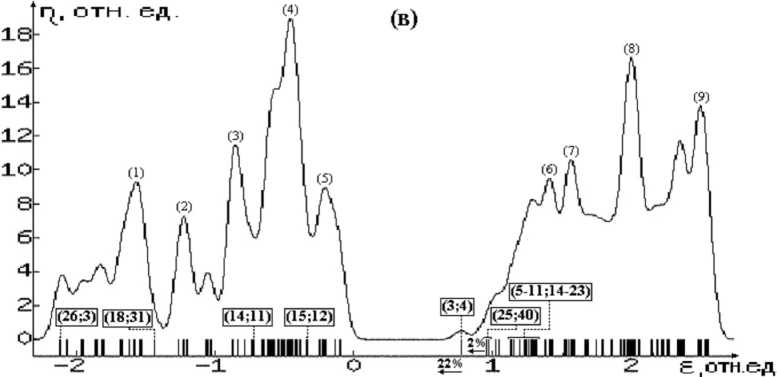
Рис. 3. Окончание

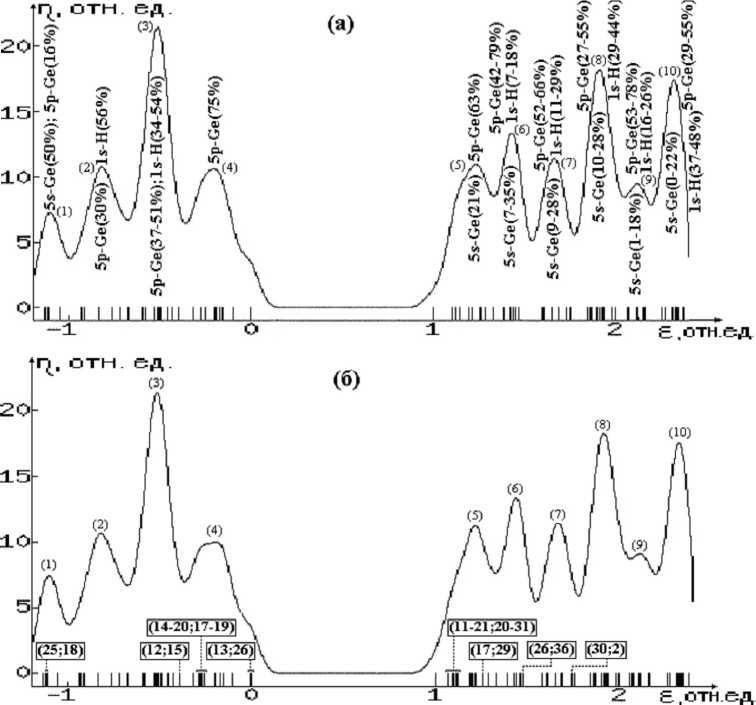
Рис. 4. Плотности электронных состояний *) германий-водородных МСНР:

(а) - без дефекта; (б) , (в) - с дефектами замещения Ge(Ga) и Ge(As) соответственно (см. также окончание рисунка на следующей странице)

* ) См. пояснения к рисунку 2.

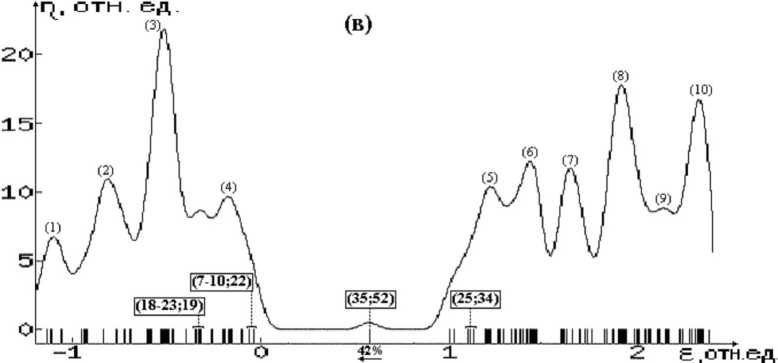
Рис. 4. Окончание

Что касается энергетического спектра КАВС, то анализ диаграмм плотностей электронных состояний изучаемых структур (рис. 2–4) позволяет сделать следующие выводы:

• 1.    В бездефектных структурах (БС) уровни энергии электронов подразделяются на группы занятых и свободных состояний (ГЗС и ГСС соответственно). В ГЗС преимущественный вклад вносят связывающие орбитали А-А и А-Н-связей, а в ГСС – разрыхляющие орбитали этих связей. ГЗС и ГСС разделены областью запрещенных состояний (ОЗС). Как следует из таблицы 3, ширины ОЗС и ГЗС уменьшаются в ряду С, Si, Ge. Отметим, что в таком же порядке изменяются ширины запрещенной зоны и валентной s , p -зоны в соответствующих С-, Si-, Ge- ковалентных кристаллах. Расположение соответствующих максимумов плотностей состояний внутри ГЗС и ГСС приведены в таблице 4 и на рисунках 2–4.

• 2.    В структурах с дефектом замещения атомов из третьей группы в случае С- и Si- КАВС в ОЗС появляются акцепторные состояния, обусловленные валентными орбиталями атомов дефекта (В и Al соответственно), отстоящие от верхней границы ГЗС ≈ на 40 % от ширины ОЗС. В случае замещения Ge → Ga такие состояния не образуются. Кроме того, внутри ГЗС и ГСС появляются состояния, обусловленные соответственно связывающими и разрыхляющими орбиталями связей атома замещения с атомами 1-й КС (рис. 2–4б).

• 3.    В структурах с дефектом замещения на атомы из пятой группы во всех КАВС в ОЗС появляются донорные состояния, обусловленные валентными орбиталями атомов дефекта, отстоящие от нижней границы ГСС ≈ на 26, 22 и 42 % от ширины ОЗС соответственно для С → N, Si → P и Ge → As дефектов замещения. Состояния, обусловленные связывающими и разрыхляющими орбиталями связей атома дефекта с атомами ближайшего окружения, образуются также внутри соответственно групп занятых и свободных состояний (рис. 2–4в).

Таблица 3 Расчетные значения ширин ОЗС и ГЗС в бездефектных угле-, кремний- и германий-водородных структурах

	C	Si	Ge
ΔE (ОЗС), эВ	11,7	7,6	7,4
ΔE (ГЗС), эВ	24,5	17,0	14,9

Таблица 4

Расположение максимумов плотностей состояний относительно верхней границы ГЗС БС (в % относительно ширины ГЗС БС), либо относительно нижней границы ГСС БС (в % от ширины ОЗС БС) для КАВС бездефектных и содержащих дефект замещения

КАВС	Номер максимума (см. рис. 2–4)
	1	2	3	4	5	6	7	8	9	10
С	66	51	36	24	12	44	67	88	147	–
С(В)	65	53	35	23	12	43	64	87	146	–
С(N)	66	52	38	25	11	45	65	86	147	–
Si	70	54	38	21	9	40	57	102	151	–
Si(Al)	70	53	39	21	9	42	60	100	148	–
Si(P)	72	55	39	21	9	42	56	100	148	–
Ge	97	72	45	15	24	42	66	91	112	132
Ge(Ga)	96	71	42	13	21	44	66	91	112	132
Ge(As)	97	71	45	14	21	42	63	90	111	130