Эллипсометрия одномерного фотонного кристалла с диэлектрическим и проводящим дефектами

Слоистые системы представляют особый интерес для многочисленных применений как для диагностических целей [5; 10; 12], так и для построения базиса новых технологических устройств в силу большого разнообразия возможных структур, обладающих различными свойствами [1; 4; 9]. Широко исследуются слоистые структуры типа D-M-D (диэлектрик – металл – диэлектрик) [2], а также M-D-M (металл – диэлектрик – металл) [3]. Одномерный фотонный кристалл представляет собой конечную систему периодически повторяющихся слоев. Важной особенностью таких сред является наличие запрещенной зоны, как и в обычных кристаллах. Наличие дефекта в таком кристалле может существенно изменить его оптические свойства [7], что может быть использовано для изучения таких дефектов [6; 8; 11]. При этом идеальная периодическая структура служит реперным фоном, на котором ярко проявляются свойства самого дефекта. В настоящей работе будет рассмотрено влияние местоположения дефекта внутри периодической структуры на угловые спектры

эллипсометрических параметров при падении на такую структуру света круговой поляризации.

1. Постановка задачи

На периодическую слоистую систему, состоящую из 10 пар слоев, под углом g падает циркулярно поляризованный свет. Рассмотрено 3 варианта расположения дефекта, внедренного вместо

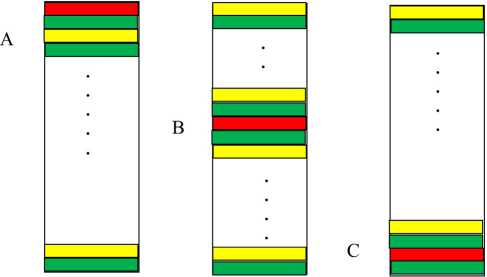
Рис. 1. Три варианта расположения дефекта в периодической структуре: A – дефект в 1-м слое; B – дефект в 9-м слое; C – дефект в 19-м слое

Fig. 1. Three variants of defect location in the periodic structure: A – defect in layer 1; B – defect in layer 9; C – defect in layer 19

®^и © Яцышен В.В., Алмохаммад Г.А., 2025

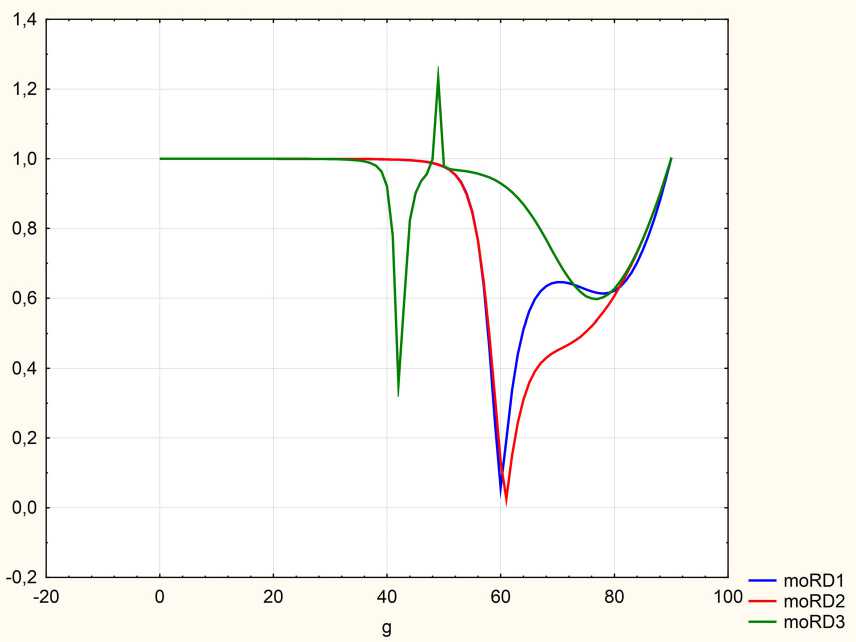
Рис. 2. Диэлектрический дефект. Угловые спектры эллипсометрических параметров ρ для 3 вариантов расположения дефекта: A – moRD1, B – moRD3, C – moRD2

Fig. 2. Dielectric defect. Angular spectra of ellipsometric parameters ρ for 3 defect location options: A – moRD1, B – moRD3, C – moRD2

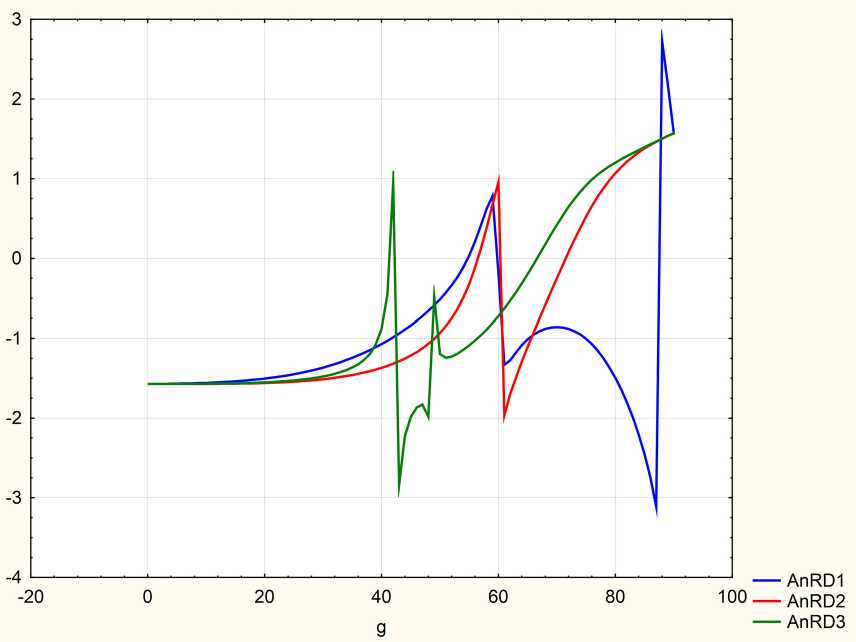
Рис. 3. Диэлектрический дефект. Угловые спектры эллипсометрических параметров ∆ для 3 вариантов расположения дефекта: A – AnRD1, B – AnRD3, C – AnRD2

Fig. 3. Dielectric defect. Angular spectra of ellipsometric parameters ∆ for 3 defect location options: A – AnRD1, B – AnRD3, C – AnRD2

Яцышен В.В., Алмохаммад Г.А. Эллипсометрия одномерного фотонного кристалла ... Yatsyshen V.V., Almohammad G.A. Ellipsometry of a one-dimensional photonic crystal ...

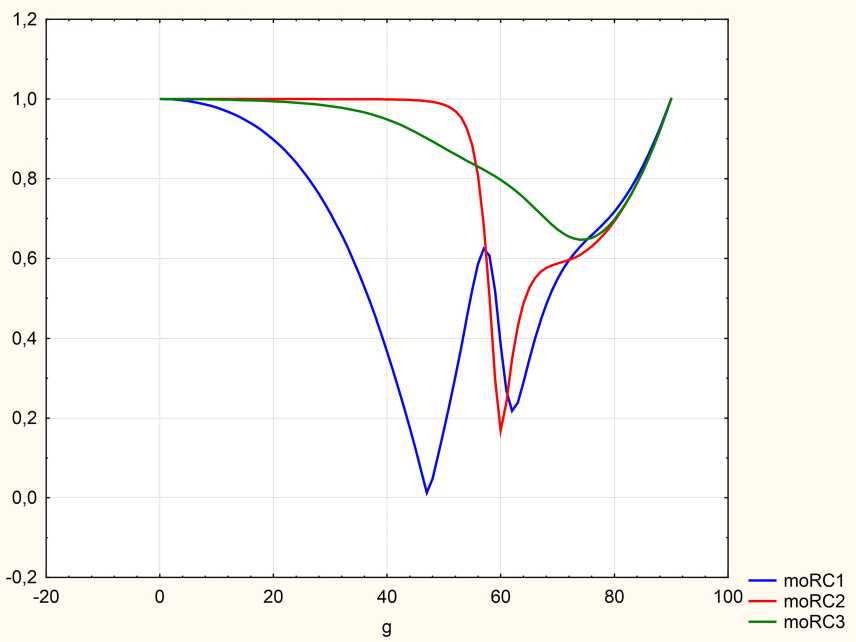
Рис. 4. Дефект с проводимостью. Угловые спектры эллипсометрических параметров р для 3 вариантов расположения дефекта:

A – moRC1, B – moRC3, C – moRC2

Fig. 4. Conductive defect. Angular spectra of ellipsometric parameters р for 3 defect location options: A - moRCl, B - moRC3, C - moRC2

исходного слоя: A, B и C (рис. 1). Требуется провести расчет угловых спектров эллипсометрических параметров для вариантов A, B, C в случаях, когда дефект представляет собой диэлектрик и когда дефект обладает проводящими свойствами – комплексная диэлектрическая проницаемость имеет мнимую часть, сравнимую с действительной.

Расчет проводился для следующих значений параметров: 1-й слой в периодической паре – диэлектрическая проницаемость S i = 5,29, толщина слоя d i = 0,0696 р , 2-й слой в периодической паре - S 2 = 1,823, d 2 = 0,1186 р , Параметры диэлектрического дефекта: s def = 2,0, толщина слоя дефекта d def = 0,069 р . Для проводящего дефекта: s def = 2,0 + 2,5 i , d def = 0,0696 р . Длина волны падающего света X = 0,64 р .

2.    Метод расчета

В качестве основного диагностического метода используется метод эллипсометрии. Эллипсометрические параметры р и Л определяются в данной работе как модуль и аргумент комплексного параметра р, являющегося отношением ам- плитудных коэффициентов отражения для p- и s-поляризации:

i Л R p

^Р = ^Р e = Rs '

В основе расчета лежит метод характеристических матриц [6; 8]. Характеристическая матрица слоистой системы представляет собой произведение характеристических матриц слоев, а амплитудные коэффициенты отражения и прохождения света выражаются через характеристическую матрицу всей системы. Получив эти амплитуды, по ним рассчитываются эллипсометрические параметры отраженного от системы циркулярно поляризованного света.

3.    Результаты расчетов

Результаты расчета представлены на рис. 1–9

4.    Обсуждение результатов

Из приведенных рисунков мы видим, что местоположение дефекта оказывает существенное влияние на угловой спектр эллипсометрического параметра р . Параметр Л демонстрирует еще

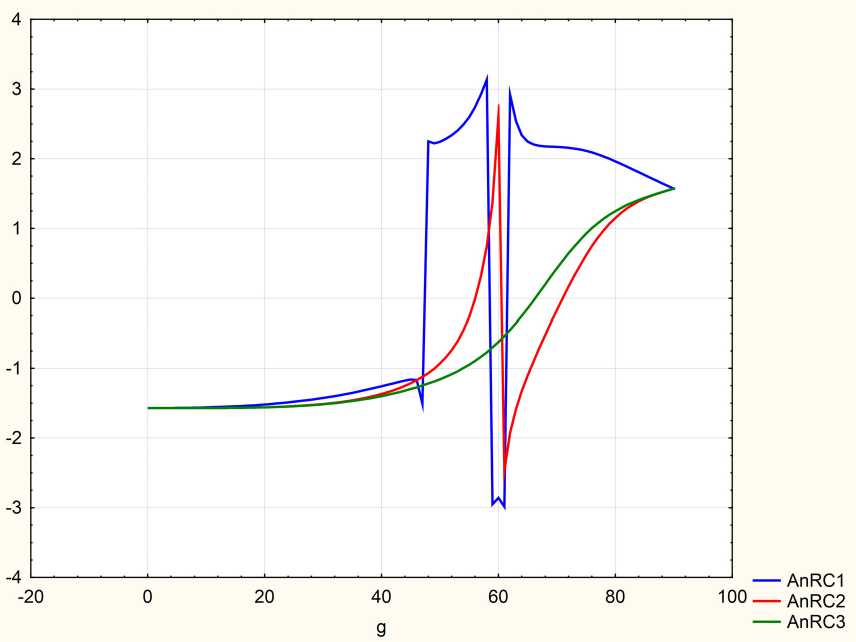
Рис. 5. Дефект с проводимостью. Угловые спектры эллипсометрических параметров А для 3 вариантов расположения дефекта:

A – AnRC1, B – AnRC3, C – AnRC2

Fig. 5. Conductive defect. Angular spectra of ellipsometric parameters А for 3 defect location options: A - AnRCl, B - AnRC3, C - AnRC2

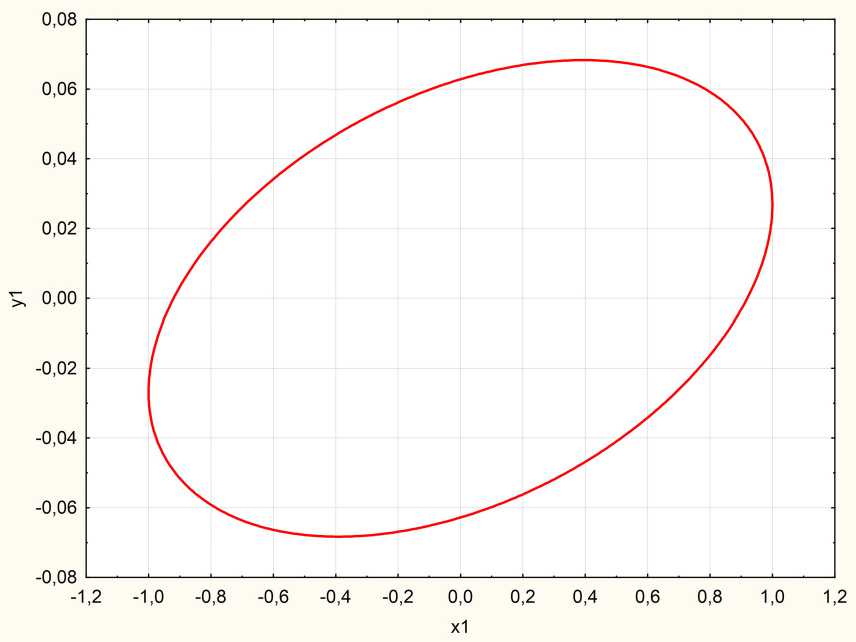
Рис. 6. Дефект с проводимостью. Правая поляризация. Эллипс поляризации g = 46 ° , р = 0,0683, А = - 1,167 Fig. 6. Conductivity defect. Right polarization. Polarization ellipse g = 46 ° , p = 0,0683, А = - 1,167

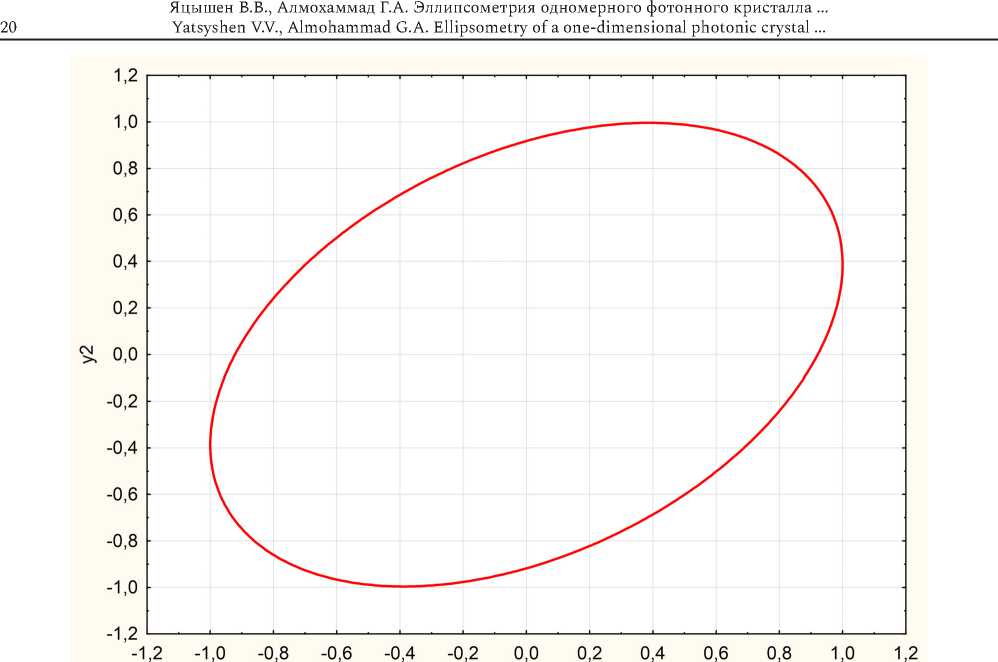
x2

Рис. 7. Дефект с проводимостью. Правая поляризация. Эллипс поляризации g = 46 ° , р = 0,996, А = - 1,172

Fig. 7. Conductivity defect. Right polarization. Polarization ellipse g = 46 ° , p = 0,996, A = - 1,172

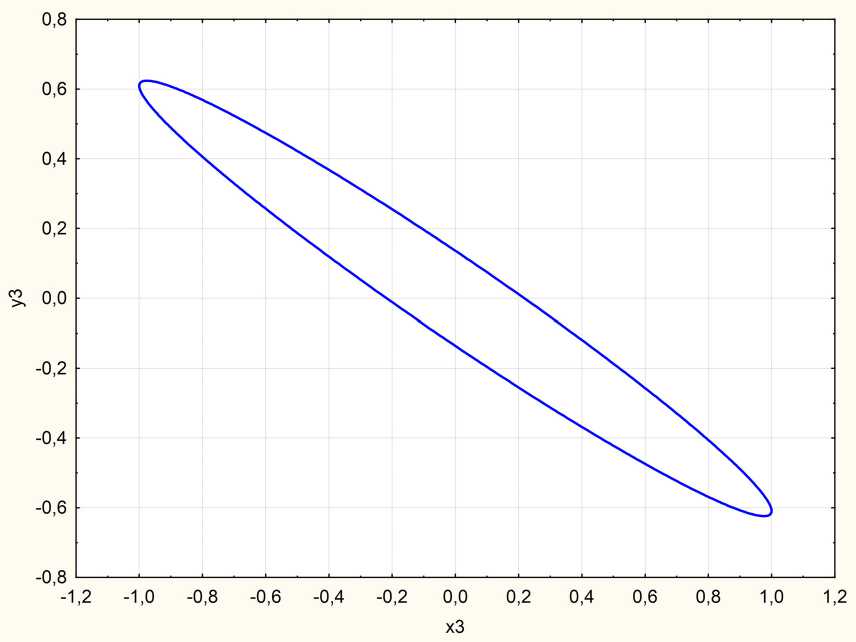
Рис. 8. Дефект с проводимостью. Левая поляризация. Эллипс поляризации g = 57 ° , р = 0,624, А = 2,922

Fig. 8. Conductivity defect. Left polarization. Polarization ellipse g = 57 ° , p = 0,624, A = 2,922

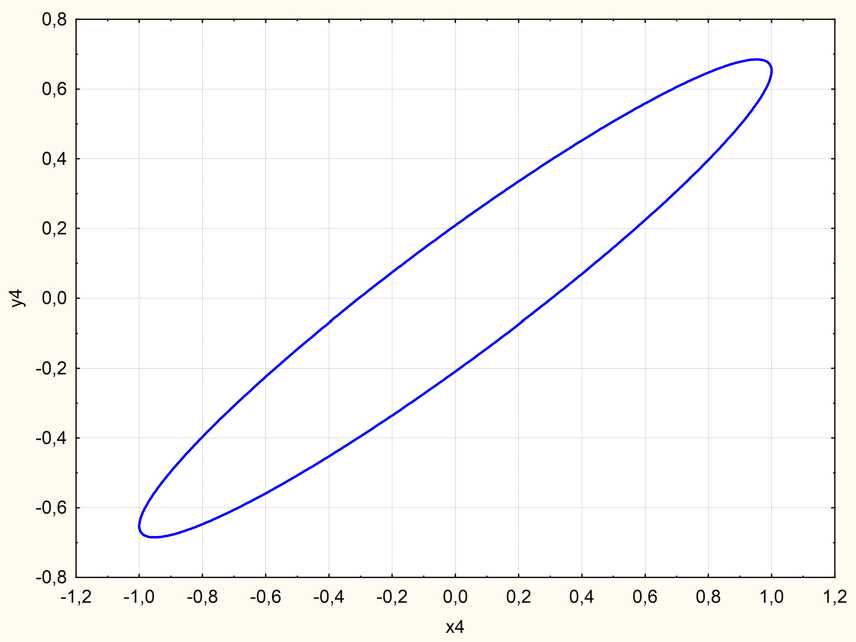
Рис. 9. Дефект с проводимостью. Левая поляризация. Эллипс поляризации g = 57 ° , р = 0,685, А = 0,31

Fig. 9. Conductivity defect. Left polarization. Polarization ellipse g = 57 ° , p = 0,685, A = 0,31

более сильную зависимость от местоположения дефекта, при этом каждое прохождение спектральных кривых через 0 в данном случае свидетельствует о смене характера поляризации с левой на правую и наоборот. На рис. 6–9 мы приводим виды поляризационных эллипсов при отражении циркулярно поляризованного света от слоистой системы с дефектом. Следовательно, анализ спектров эллипсометрических параметров с помощью циркулярно поляризованного падающего света позволяет получить детальную информацию о характере дефекта. Кроме этого, такие периодические структуры с дефектом – диэлектрическим и проводящим – могут служить основой для преобразователей поляризации света.

Заключение

В работе показана высокая чувствительность эллипсометрических параметров отраженного света от характера и местоположения дефекта в периодической структуре при падении на нее циркулярно поляризованного света. Продемонстрирована возможность управления характером поляризации отраженного света с помощью периодической структуры с дефектом.