Эмпирическая модовая декомпозиция пульсовых сигналов

Наиболее эффективным методом обработки и анализа биомедицинских сигналов является спектральный анализ, основанный на преобразовании Фурье и вейвлет-преобразованиях. Преобразование Фурье относится к классу ортогональных преобразований, в котором используется фиксированный, заранее заданный базис гармонических функций, не зависящий от вида анализируемой кривой. В результате преобразования Фурье получаем параметры, характеризующие некоторое усредненное состояние процесса в заданном интервале времени.

Одним из часто используемых методов исследования биомедицинских сигналов является метод, основанный на вейвлет-преобразованиях. Вейвлет-преобразование, так же как и преобразование Фурье, производит разложение в фиксированном базисе функций. Этот базис должен быть предварительно задан, т.е. должна быть выбрана вейвлет-функция, используемая в процессе преобразования. Существует много видов функций, используемых в качестве базиса, и в зависимости от этого базиса результаты преобразования одного и того же сигнала могут сильно отличаться друг от друга. В связи с этим возникает много неопределенностей в интерпретации полученных зависимостей.

Оба метода, как показала практика, достаточно универсальны и могут применяться в различных областях. При решении многих задач, в первую очередь при анализе стационарных процессов, методы дают хорошие результаты, но для более подробного исследования сигналов и выявления скрытых закономерностей необходимо использовать такой метод, который не только позволял бы работать с нестационарными процессами, но и использовал бы адаптивный, определяемый исходными данными базис преобразования.

Наиболее перспективным методом исследования сигналов является метод, основанный на модовой декомпозиции сигналов и преобразовании Гильберта. Преобразование Гильберта-Хуанга [1] представляет собой частотно-временной анализ данных (сигналов) и не требует априорного функционального базиса преобразования. Метод был предложен Н. Хуангом в 1995 г. с обобщением на анализ произвольных временных рядов коллективом соавторов в 1998 г. [1, 2, 3]. Достоинством данного метода является высокая адаптивность, связанная с тем, что базисные функции для разложения сигнала конструируются непосредственно из самого исследуемого сигнала. Это позволяет учесть локальные особенности сигнала, внутреннюю структуру и присутствие различных видов помех.

Преобразование Гильберта-Хуанга состоит из двух этапов. На первом этапе при помощи данного алгоритма находятся эмпирические моды, или внутренние колебания. Затем на втором этапе при помощи преобразования Гильберта на их основе определяется мгновенный спектр исходной последовательности. В данной статье более подробно остановимся на алгоритме эмпирической модовой декомпозиции сигналов.

Методика. Результаты и обсуждения

Mетод эмпирической модовой декомпозиции основан на предположении, что любые данные состоят из различных режимов колебаний (колебательных процессов). Каждый режим представляет собой простое колебание, которое в определенной степени «симметрично» относительно локального среднего значения и, следовательно, имеет экстремумы и нулевые пересечения. Каждый из этих колебательных режимов может быть представлен функцией внутренней моды со следующим определением [1]:

• 1.    Количество экстремумов и количество нулевых пересечений должно или быть равным, или отличаться самое большее на единицу.

• 2.    В любой точке данных среднее значение огибающих, определенных локальными максимумами и локальными минимумами, является нулевым.

Таким образом, в процессе декомпозиции производится разложение на модовые функции (intrinsic mode function ‒ IMF), которые не заданы аналитически и определяются исключительно самой анализируемой последовательностью. В основе алгоритма лежит построение гладких огибающих по максимумам и минимумам последовательности и дальнейшее вычитание среднего этих огибающих из исходной последовательности [3]. Для этого производится поиск максимумов и минимумов и строятся сплайны, проходящие через эти точки. Эти сплайны и образуют верхнюю и нижнюю огибающие. Рассмотрим действие алгоритма при анализе реальной пульсовой волны. На рисунке 1 представлены анализируемая последовательность f(x), огибающая максимумов и огибающая минимумов. Пунктирной линией представлена средняя линия m 1 (x), которая вычисляется по огибающим:

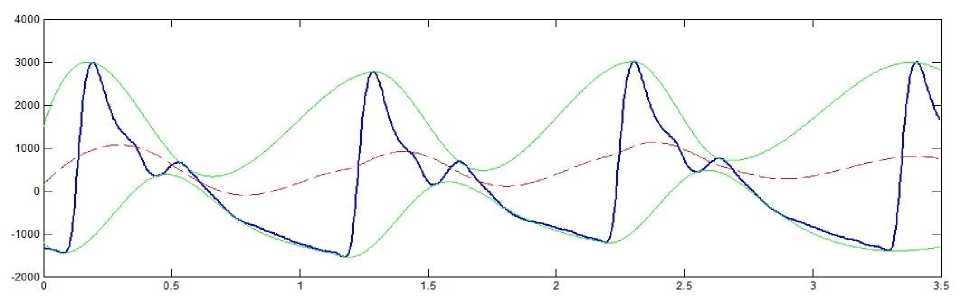
Рис. 1. Построение огибающих и средней линии

Найденное таким образом среднее значение m 1 (x) вычитается из исходной последовательности f(x):

h i ( x ) = f (x ) - m i ( x ) •

Таким образом получаем первое приближение к первой модовой функции. Далее повторяем вышеописанные процедуры, принимая вместо исходной функции f(x) функцию h 1 (x). Получаем второе приближение к первой модовой функции h 2 (x):

h ₂ ( x ) = h ( x ) — m ₂ ( x ) •

Аналогично находим третье и последующие приближения к первой модовой функции IMF:

h ^{( x}) = h — 1 ^{( x} ) ^— m i ^(x) •

Критерием останова итераций является задание предела по нормализованной квадратичной разности между двумя последовательными операциями приближения, поскольку функции m i (x) и h i (x), стремятся к неизменяемой форме по мере увеличения количества итераций.

В результате перечисленных шагов находится первая модовая функция, которая является наиболее высокочастотной компонентой сигнала:

c i ^(x) = hk ^{( x})

После вычитания первой модовой функции c 1 (x) из исходного сигнала мы оставляем в нем более низкочастотные составляющие:

r i^{( x}) = f ^{( x}) ^— c i ⁽ x ) •

Для нахождения второй и последующих модовых функций c i (x) функцию r 1 (x) принимаем за исходный сигнал и повторяем все вышеизложенные процедуры. Процесс повторяется до тех пор, пока не будет достигнут критерий его останова, когда остаток имеет не более двух экстремальных точек.

Таким образом мы разложили исходный сигнал f(x) на набор модовых функций:

n f (x) =Z ci (x) + rn (x) .

i = 1

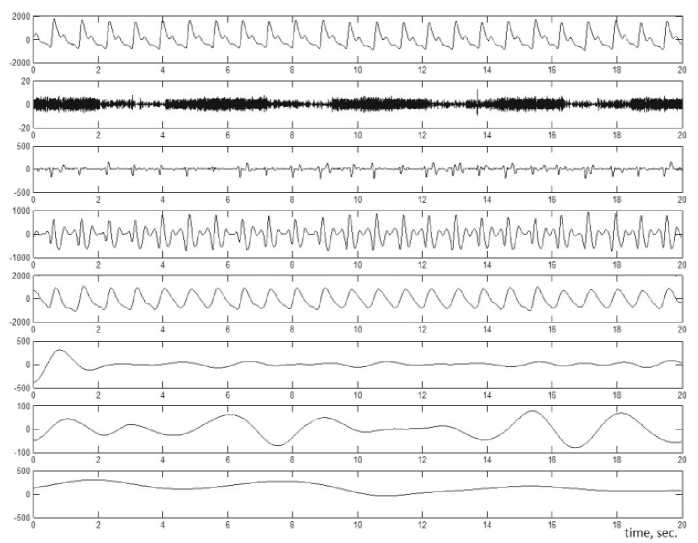
Рис. 2. Эмпирические модовые функции c i (x) пульсового сигнала

На рисунке 2 представлены модовые функции пульсовых сигналов, которые будут подвергнуты преобразованию Гильберта для оценки частотного состава.

Как видим, описанная процедура эмпирической модовой декомпозиции не базируется на строгих математических выкладках, а полностью является эмпирической. В процессе декомпозиции получается семейство IMF-функций, упорядоченных по частоте. Каждая последующая IMF-функция имеет более низкую частоту, чем предыдущая.

Выводы

Предложен новый метод исследования пульсовых сигналов, основанный на модовой декомпозиции сигналов и преобразовании Гильберта, представляющий собой частотно-временной анализ сигналов и не требующий априорно заданного функционального базиса преобразования. Метод является, на наш взгляд, перспективным и позволит более эффективно выявлять локальные особенности сигналов и их внутреннюю структуру.