Энергетическая оценка процесса пылеулавливания в циклонных аппаратах

Важную роль в данном процессе играет установление закона изменения величины разрежения и тангенциальной скорости потока в произвольном поперечном сечении конической части циклона. Исследования процесса пылеулавливания в циклоне основаны на трех законах [1, 2].

Первый – закон сохранения расхода: количество жидкости, прошедшей через площадь в секунду, то есть массовый расход, остается постоянным по всей трубке потока.

Второй – закон неизменности момента количества движения: произведение скорости вращения воздушного потока υ вр на радиус вращения R сохраняется постоянным от одной струйки воздуха к другой. Вращающийся газовый поток – это «антикарусель»: чем меньше радиус вращения, тем больше скорость.

Третий – закон сохранения энергии единицы объема газового потока (уравнение Бернулли): в установившемся движении идеальной жидкости сумма потенциальной энергии единицы объема, то есть давления и кинетической энергии, обусловленная скоростью, сохраняется постоянной вдоль струйки потока.

Для установления данного закона принимаем, что воздушный поток есть однородная газовая среда, имеющая скорость υ, давление р и плотность ρ.

Геометрические размеры циклонного аппарата представлены на рисунке. Обозначим за Z – ось циклона, пусть начало координат расположено в основании аппарата в точке О. Проведем через точки ABCDM плоскость, перпендикулярную оси циклона, в сечении имеем круг радиусом R ст ( R ст изменяется от R 2 до R ), обозначим переменный радиус – r (от 0 до R ст ). Высоту поперечного сечения конуса – за Z 1 . Угол между образующей конуса и осью циклона – γ .

Исходя из представленного рисунка, выведем ряд соотношений.

RR

tg(Y) =   „ ² => Y = arctg

HК

Из треугольника ΔMDN (рисунок) следует

RR

tg( r) =  ст z 2

RR

H К

.

.

Приравнивая значения tg(γ) из первого и второго соотношения, получим

Z

R R      R R.

ст       2                     2

к

Тангенциальная (касательная) скорость ся закону площадей, т. е.

cos( ) спирального потока подчиняет- та нг

L f,

где L – объемный расход воздуха, м³/с; f – площадь элементарного потока, м².

Площадь потока определим по формуле

f             R dr

[ df -a-r- [ — => f = a-r - (In R -ln R ) ст .

O             Rст r

Или

f = a-r -ln( R I R_cm ),

где а – высота спирального потока, м;

R – радиус циклона, м;

R ст – радиус конической пристенной части циклона, м; r – переменный радиус в произвольной точке, м.

Движение воздушного потока в кольцевом пространстве циклона является установившимся безвихревым циркуляционным потоком. Определим связь между скоростью, давлением и плотностью воздуха в произвольной точке спирального (вихревого) потока, для этого

используем интеграл Д. Бернулли

3 ²   P dP

--1-  — = const.

²    Р ст P

Принимаем касательный подвод воздушного потока в циклон при угле наклона входного патрубка α1 = 0, следовательно, cos(α1) = 1 и        . При изотермическом процессе очи стки воздуха согласно уравнению состояния идеального газа имеем

PP .                                            (5)

P         ст P ст      ст                     ст

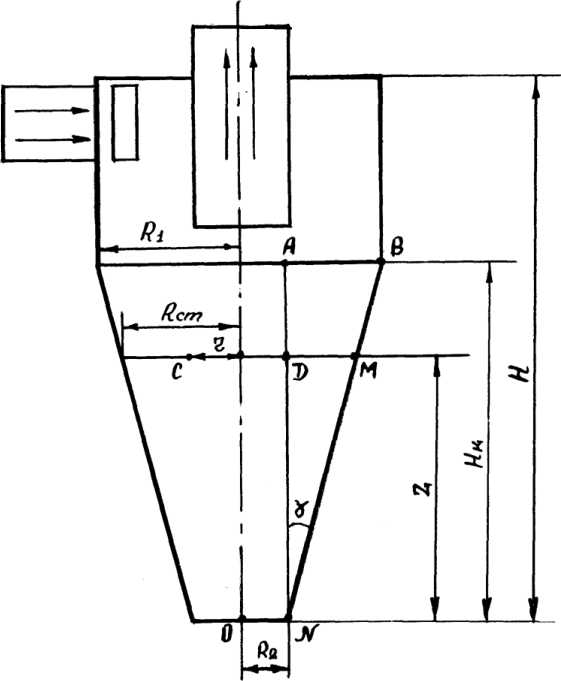
Расчетная схема циклонного аппарата

Подставим ρ из (5) в (4)

² Р ^P dP ст           _{C .}

O

2     ст Pст P

Вычисляя интеграл (6), получим

P

2P ст ln

ст

P

P

ст

= с

O .

Постоянную интегрирования С О определим из граничных условий

Р = Р ст , и = U cm при Г = R em , ТОГДа

с ² т

О ₂

Из формулы (2) следует

rC  R

O      ст с

R ст ст

r

Подставив значение скорости потока из (9) в уравнение (7), получим

1 <  S R Л P , ст ст         ст • In

21 r ) p ст

P ]   i9²

ст

P ст

.

Преобразуем выражение (10), получим зависимость

P P exp ст

9² -p L R² ) ст    ст          ст

2- P I r² > ст

, Па.

Зависимость (11) характеризует изменение величины давления в циклоне по продольному радиусу – от стенки корпуса R ст до радиуса r (рисунок).

Проанализируем зависимость (11). Рассмотрим два случая.

Первый , при котором r = R ст , в этом случае P = P ст , давление на поверхности конической части определяется пристенным значением Р ст .

Второй, при r -> 0, т. е. при приближении радиуса r к центральной оси циклона величина давления в этом случае асимптотически приближается к положительной бесконечности, что практически не реализуемо и такое состояние характеризует ограниченное применение формулы (11) в области осевой части циклона.

Изменение разрежения воздуха в поперечном сечении конической части циклона на основании формулы (11) запишем в виде

^P ( r ) = P m ^exP -

P2 "A ст ст

2- P ст

'     Rc;,)

ст r² ,

, Па.

Тангенциальная, пристенная, скорость воздушного потока в поперечном сечении конической части циклона определяется из формулы (11) по зависимости ст

2-P  

ст

( R² R_ст

' r^{2 r}

, м/с.

При разрежении воздуха в циклоне тангенциальная скорость воздушного потока согласно формуле (12) будет равна ст

2-P -^P— lnP " ст                 ст

( R2

R_ст

I r²

, м/с.

При подстановке в формулу (14) выражения (9) получим зависимость тангенциальной скорости потока от перечисленных величин

9 (r ) = 9 R^^

ст

r

2-P  

Rm-A

I r² .

После преобразования формула (15) запишется в виде

AZ X A A 2-P -P-1П P     ,

9 (r) = 9 -R • ---с^Ц---с^²¹^, м/с.

’ ст   с2       р .(R2 -r2)    , ст     ст

Если вместо Rст подставить в (15) соотношение (1), получим формулу для расчета тангенциальной скорости воздушного потока в поперечном сечении конической части циклона в зависимости от высоты сечения аппарата Z и переменного радиуса r

1Р ЛпР-1п Р 1

-----ЁГ-ст(-----------ст Т1 х •                      (16)

\Рст^{{ R}2 ^HK^^{Z (R}-^R2) J -r }

При подстановке в формулу (16) значения r = 0 (ось циклона) максимальная тангенциальная скорость потока будет рассчитываться по формуле

2P (inP-inP )   , ст             ст , м/с.

ст

Таким образом, измеряя пьезометром разрежение Р и Рст в зависимости от радиуса r, можно рассчитать по формуле (16) теоретическую тангенциальную скорость потока в поперечном сечении при высоте сечения Z и переменном радиусе r. Фактическая тангенциальная скорость потока устанавливается экспериментальным путем, может быть рассчитана по формуле (15) или формуле (16) путем введения поправочного, опытным путем установленного коэффициента.

Обобщенная формула расчета величины разрежения в поперечном сечении конуса в зависимости от Z и r запишется в виде

^P(Z, r) = Рст exp

3²r²p_{cm x}  [R₂Hк +Z(R — R₂)]²

2R² P            [rH ]²

ст ст                      к

Зависимость (18) учитывает параметр Z – высоты сечения, в котором строится эпюра разрежений, а также геометрические параметры циклона – радиус циклона (R) и высоту конической части аппарата (HК). Разбивая высоту конуса на равные отрезки (переменная Z), можно построить эпюры в заданной плоскости.

Скорость в ядре вихря – центральной оси аппарата будет равна v (0) =

2-P -ln(PIP ) ст            ст

ст

Из формулы (19) следует, что скорость потока в осевой части циклона не зависит от высоты поперечного сечения Z и конструктивных параметров конической части аппарата. Ядро вихря имеет постоянную и максимальную скорость газового потока по оси аппарата (при стационарном режиме пылеочистки). Преобразуя выражение (19), имеем

O V .2        ( P A

E^⁰-^ ₌ p in — .                         (20)

ст ст

Умножим левую и правую часть выражения (20) на массу воздушного потока – m, получим выражение для расчета кинетической энергии ядра потока m y2

m

mP

=--P in —

ст ст

P

Е vPP in — .

ст

P

Исходя из газового уравнения Менделеева – Клапейрона (уравнения состояния газа PV RT ), кинетическую энергию потока (при массе потока m = 1 кг) рассчитывают

E = RT-in — , Дж,

P ст где R – газовая постоянная для воздуха R = 287 Дж/(кг∙К);

• T – температура газового потока, К;

• Р – давление потока в ядре вихря, Па;

Рст – давление потока в пристенной части циклона, Па.

В результате теоретических исследований получены математические модели, учитывающие аэродинамические и конструктивные параметры процесса пылеулавливания. Зависимость (22) позволяет рассчитать кинетическую энергию воздушного потока процесса пы- леулавливания в циклоне.