Эволюция космологической модели с вращением с метрикой типа II по Бьянки

Согласно наблюдений телескопа "Планк", статистическая значимость аномалии – глобальной анизотропии – остается низкой и результаты телескопа "Планк" полностью удовлетворяют Стандартной космологической ЛCDM - модели [1]. Так что на данный момент общепринятая точка зрения состоит в том, что наша Вселенная однородна и изотропна.

Однако известны астрономические наблюдения, которые могут свидетельствовать в пользу крупномасштабных отклонений от изотропии в наблюдаемой Вселенной.

Первый тип наблюдений касается исследования векторов поляризации электромагнитного излучения, пришедшего от далеких квазаров [2]. Оказалось, что вектора поляризации ориентированы не случайным образом, а имеют преимущественное направление [2]. Причем это направление явно проявляется для тех векторов, которые соответствуют достаточно удаленным квазарам.

Второй тип наблюдений связан с так называемыми спиральными галактиками. Согласно последнему анализу [3], в одной части небесной сферы преобладают влево закрученные галактики, в другой части – закрученные вправо. На основе этой асимметрии была

найдена выделенная ось в пространстве. Укажем здесь, что есть особый тип анизотропии в 4-мерном пространстве – это анизотропия, обусловленная космологическим вращением. Поэтому в современной космологии сохраняют актуальность исследования возможного вращения Вселенной. Укажем некоторые из работ, посвященных космологическому вращению [4, 5, 6, 7].

В данных работах рассматриваются следующие космологические метрики: обобщение метрики Гёделя, метрики типов II, VIII по Бьянки, и используются различные источники тяготения. При теоретическом моделировании космологического вращения целесообразно использовать метрики различных типов по Бьянки, которые не противоречат наблюдательным данным.

Отметим, что в современной космологии весьма актуально исследование темной энергии (неизвестной субстанции, которая приводит к ускоренному космологическому расширению), а также темной материи [8, 9].

В данной работе в рамках общей теории относительности построен космологический сценарий с вращением на основе метрики типа II по Бьянки вида ds2 = dt2 - 2 R (t) 4be(1) dt -

- R ² ( t ) [ A ( e ⁽¹⁾ ) ² + ( e ⁽²⁾ ) 2 + ( e ⁽³⁾ ) 2 ] °)

где

A, b - const , A >  0, b >  0,

e ⁽¹⁾ = dx — zdy , e ⁽²⁾ = dy , e ⁽³⁾ = dz .

Источниками гравитации являются 3 жидкости с соответствующими уравнениями состояния.

Построенная космологическая модель отлична от ранее найденных космологических решений для метрики (1).

Нестационарная космологическая модель с вращением

Итак, будем искать для метрики (1) космологическое решение уравнений тяготения Эйнштейна, записанных в тетрадной форме

^ — 1 n R = к T .      (2)

У нас используется лоренцевая тетрада и выбрано N = 1, c = 1.

Тензор энергии – импульса сопутствующей анизотропной жидкости в тетрадном представлении имеет вид ~~

T ) = ^{( n} + P ) u~k + ( ° ^{— n} ) X i X k ^{— n}n ik , ⁽³⁾

где n, ° - компоненты давления анизотропной жидкости, р - плотность энергии анизотропной жидкости, Xi={0,1,0,0} - тетрадные компоненты пространственноподобного вектора анизотропии, и ‘ = 8  - вектор 4- мерной скорости сопутствующей анизотропной жидкости в проекции на тетраду.

Тензор энергии – импульса несопутствующей идеальной пылевидной жидкости

T^ = s uu k ,           (4)

Tk = T (° + T + T ( ³⁾.         (6)

ik       ik        ik        ik

Из закона сохранения тензора энергии – импульса и отсутствия взаимодействия между

данными жидкостями следует, что ковариантная 4-мерная дивергенция должна быть

равна нулю для каждого из слагаемых в (6).

Это приводит к следующим условиям (в

координатной форме):

T Г⁽¹⁾ = о,

T _p ^{v (2)} = 0 .                 (8)

Из

уравнений (7) и (8) получено

U[ = U =

^s 1

где е - плотность пыли, и - тетрадные ком-

поненты ее скорости.

Тензор энергии – импульса несопутствующей идеальной ультрарелятивистской жидкости

Ti ⁽³⁾ = S + Р ) ~ ~к — Р П = ⁴ S и и и_к — ^{S 1} п_к ,

Ik        \  1         i к К         * Ik      А 1 Ik      О ^f ik

1 Р = f J ,             (5)

где г_х - плотность энергии, p - давление, и_{ – четырехмерная скорость данной жидкости.

В системе уравнений Эйнштейна (2)

4 A + b

b

л

;^;0;0 ,

\

~

4 , fe >  0 ), R

^s = 4-, ^(s 0 > ^{0 ) ,} R

здесь s , s ₀ — const.

Законы (10) и (11) соответствуют

зави-

симостям плотностей энергии от масштабного фактора во фридмановских космологических моделях.

Система уравнений (2) с учетом (3)–(9) примет вид

—

8 RRb + 12 R ² A + 8 R ² b — A ² + Ab + 2 b²

2 , 4 „ ~2

= £ U 0 +   ^s 1 U 0

4 R ²( A + b )

—

s 1

3 ^{P ,}

— 4 t > ( 4 RR — 4 R ² — A — b ) 2 R² 4 A + b

= ииц^ + —,(12)

• —    8 RRA — 8 RRb — 4 RR ² A + 8 RR ² b + 3 A ² + 5 Ab + 2 b ² _

4 R 2( A + b)

2   4 ~2

su< +s u} ++ °, 13

• —    8 RRA — 4 R2 A — A2 — Ab

  ---------z-------------= — + n .

4R2(A + b)3

Из этой системы с учетом (10) и (11) получено t = f        ^RdR        ,(13)

^J 46 ~ R ⁴ — 6 a R ² + 4 0 R + 3 /

A + b _n  ~ ( A + b )     2~ ( A + b )

a =----; в = —-----; у = —-----,

4        2 A3

~ = const .

Интеграл (13) не выражается в элементарных функциях, однако можно качественно исследовать решения на различных космологических стадиях.

Космологическое вращение у нас понимается как вращение поля 4-мерной скорости жидкости. Ввиду того, что в нашей модели вращается только темная энергия (моделируемая анизотропной жидкостью), будем "сохранять" ее на всех стадиях, в то время как на стадии преобладания ультрарелятивистского вещества

£ положим в системе (12) £ = 0, £ = —j, а на

R4

стадии доминирования пылевидной материи будем пренебрегать ультрарелятивистским £ веществом: £ = 0, £ = -°-.

¹            R³

Стадия преобладания ультрарелятивистского вещества

Считая, что на данной стадии:

£

£ = 0, £ = -°-, из (12) можно получить

R ⁴

У нас

3Ac  A £ _ 3Ac

A + b  R ’ R4 >> A + bR' ’

Будем полагать, что

3 Ac

>>^.

A + bR

Тогда из (18) имеем t =

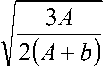
J

2 RRdR

HAf  3AГ ’

+ \ A + b 4 R² R ⁴

и можно получить

,  ³ A • [ RdR

V ( A + b ) c₀^J

В итоге на стадии доминирования ультраре-лятивистского вещества имеем R ~ V t .

Стадия преобладания пылевидного вещества

Считая, что на данной стадии

— 3 A c n =---- A + b

3 AcR

, c >  0,

^£ 1

£

= 0, £ = —0-, из (12) можно получить

R ³

p =

² — A ( A + b )

R ²( A + b )

,

3 A C ~ _A ------, c >  0.

+ b

—

a =

3 AcR ² + A ( A + b ) R ²( A + b )     ’

Уравнения состояния анизотропной жидкости для разных компонент давления имеют вид

A n + p =y ,a + p = 0.    (15)

R ²

При этом R=R(t) удовлетворяет уравнению:

3 A c R ² — A ( A + b ) R ²( A + b )    ’

— 3 A C R ² + A ( A + b ) R ²( A + b )

Уравнения состояния анизотропной

где

RR ³ — R ² R ² — a R ² + в = 0 ,

жидкости для разных компонент давления имеют вид (15) и в этом случае.

При этом R(t) удовлетворяет уравнению:

A + b _n 2~ ( A + b ) a =---; в = —-----

4     ¹       3 A

.

Решение уравнения (16) дает f    2RRdR t = i

^J 72~ R ⁴ — 2 a R ² + в

.

На стадии доминирования ультрарелятивист-ского вещества, считаем, что c

А       ^£0

£ = °, £ 1 = -4 , £ 1 >>  р .

R

'RR2 — R2 R — aR + в = 0,(24)

где a = A+b; в = £p + b).(25)

Решение уравнения (24) дает f3RRdR t = J /     ;                .

^J V3C R ³ — 3 a R + 2 в

На стадии доминирования пылевидного вещества считаем, что

£

£ = 0, £ = -⁰- , £ >>  p .

¹            R³

У нас сейчас 3 Ac ^~ A

P =7.

A + bR

Пусть

3 AC   A  z3

---->> —г, —0- >>-----

A + b   R ²  R³

Тогда из (26) им еем

A3

\ a+b J  3A~  3A

Ra ++ -O-

\ A + b  4 R2

и можно получить

t к	--—f R/Ш. (A + b ) £ о  J

В итоге на стадии доминирования пылевидной материи: R ~ t ^2/3 .

расширение	3 R ® = У
	b
вращение	Ш = —, 2 R
	4bF L
ускорение	a =   .          ■
	4 A + bR

Сдвиг отсутствует. Параметр расширения пылевидной жидкости у нас равен ~ 3 JAR w = , -, вращение, и сдвиг, и ускоре-4 A + bR ние для пыли отсутствуют. Таким образом, наша модель описывает фридмановский этап эволюции Вселенной с последующим переходом к ускоренному экспоненциальному расширению.

Стадия доминирования темной энергии

Считая, что на данной

£

£ = 0, £ = —0- и р >> £ , имеем

1              _R 3               ^,

стадии

3 Ac ^~

P - £ =---- A + b

-

A

R ²

-

^ >> 0. R3

Тогда из (29) получим

t

Тогда

1 dR 1 dR

Л ^J R ~ H ^J R ‘ R ~ e^Ht , ( h = ~ ) ) .

Заключение

Кинематические параметры анизотропной жидкости (темной энергии) в нашей модели имеют вид: