Justification for measurement equation: a fundamental issue in theoretical metrology

Abstract A review and a critical analysis of the specialized literature on justification for the measurement equation and an estimation of a methodical error (uncertainty) of the measurement result are presented in the paper, and some prospects for solving of the issue are discussed herein. Keywords Physical and mathematical model • Measurement equation (model equation) • Error • Uncertainty • Algorithm Imprint Aleksandr V. Prokopov. Justification for measurement equation: a fundamental issue in theoretical metrology; Cardiometry; No.3; November 2013; p.58-68 ; doi: 10.12710/cardiometry.2013.3.5868 Available from:

Statement of the problem and analysis of publications. In recent years the measurement equation (model equation) has become an object enjoying close attention by researchers in metrology in many countries throughout the world. The measurement equation in metrology is interpreted [1, 2] as a functional relationship linking the quantity intended to be measured (measurand) with the quantity values immediately measured, as well as other quantity values which are essential for the measurement procedure under consideration. The measurement equation is required for solving many metrological issues, particularly for development of new measurement methods and measuring instruments, including an analysis of measurement result accuracy.

The problem of measurement modeling is widely represented in scientific programs of the UK’s National Physical Laboratory (NPL) devoted to the development of mathematical models and software for metrology applications [3], and issues on modeling measurement equations have a significant place in papers by German [4 - 6], Russian [2, 7 - 10] and Ukrainian [11 - 18] metrologists. It should be noted that most papers give an analysis of the already known models to select the best suited measurement equations. At the same time, the general principles of justification for the equation of measurement and an estimation of a methodical error (uncertainty) of measurement result are still insufficiently treated.

In the specialized literature on the subject, an extreme complexity of the issue on derivation (justification) of the measurement equation is emphasized; among other things, it is suggested that some specific approaches relating basically to arts rather than science should be required to derive the measurement equation [2]. It is also argued [8] that the measurement equation is one of the components of a priori knowledge obtained not by the procedures known from the point of view of metrology, but produced by methods used in some allied sciences. Perhaps that is the reason why there are no instructions in the Guide [1] on how to justify the measurement equation for metrological analysis. Instead, such unusual for scientific and technical literature recommendations as to rely on "critical thinking", "intellectual honesty" and "professional skill" are used therein.

It should be noted that the authors of the Guide to the Expression of Uncertainty in Measurement [1] are aware of the necessity to improve this document. A few years ago, a special working group WG1 was established under the Aegis of the International Bureau of Weights and Measures (BIPM). One of the main tasks of this Group is to prepare specific Supplements to the Guide, including a separate Supplement (JCGM 103) dedicated to the measurement procedure modeling and methodology of the measurement equation justification [19].

Thereby it confirms the fact that the problem of a rigorous justification for an algorithm of obtaining the measurement equation remains highly topical, and the given problem is a subject of the theory of measuring which should be referred to the fundamental issues in metrology.

The aim of this paper is to review and criticize the existing publications on the measurement equation justification and estimation of a methodical error (uncertainty) of the measurement result as well as discuss some promising ways for solving this problem.

Summary and outlines

The developments [4-6, 11-18], where the main aspects of the above problem are analyzed and general outlines for obtaining the measurement equation are provided, can be considered as a remarkable step on the way of finding the proper solution to the above issue. In the papers [4-6], for example, an outline of this sort consists of five successive stages which are as follows:

• I.    Description of the measurement, identification of significant quantities (including the measurand and influence quantities) and applied method of measurement.

• II.    Analysis of the measurement, its decomposition into separate elements , graphical representation of the cause-and-effect relations between the elements for a certain ideal (not exposed to external influences) measurement within the scope of the standard modeling components.

• III.    Consideration of all distortions, effects of an incomplete knowledge of quantities and external factors capable of affecting the ideal measurement. Graphical and mathematical interpretation of the cause-and-effect relations for the real (exposed to external influences) measurement. Use of corrections for taking into account distortions (external influences).

• IV.    Identification of reciprocal influence of quantities, introduction of correlations.

• V.    Transformation of mathematical relations which describe the cause-and-effect relationship for obtaining the model equation.

It should be pointed out that the operations necessary for the mathematical formulation of the problem are not specifically treated in the above mentioned publications.

In articles [11 - 18] an algorithm of obtaining the measurement equation is represented by seven stages as given below (you can find below the description of the algorithm for the case with the only one quantity to be measured to simplify the matter, and for the case with measuring more than one quantity the procedure should be similar):

• I.    Selection of a measurement object and preliminary identification of its properties and attributes which are essential for formation of a data signal carrying information relevant to the quantity value to be measured (unknown quantity value). Concretization of the said quantity.

• II.    Preliminary identification of physical processes which may influence the data signal and lead to a change in the latter during signal traveling from the object of measurement to the measuring device including traveling of the signal within the measuring device. Selection of quantities to be immediately measured.

• III.    Formulation of a set of equations (with appropriate initial and boundary conditions) to describe the physical processes responsible for forming the data signal and influencing the latter during traveling of the signal from the measurement object to the measuring device including traveling of the signal within the measuring device (the mathematical formulation of the problem).

• IV.    Analysis of the initial equations. A quantitative assessment of influence of individual physical effects and processes on characteristics of the data signal during transmission of the signal from the measurement object to the measuring device, including transformation of the signal in the measuring device. Simplification of the mathematical formulation of the problem based on elimination of some physical effects and processes, which are insignificant for a given level of accuracy, from consideration. Evaluation of an error (uncertainty) caused by the said negligible effects and processes.

• V.    Selection and justification of the methods for solving the simplified equations for solving the problem which allow establishing the relationship between the unknown quantity (the measurand) and the immediately measured quantity values. Generally, this relationship may contain known constants, parameters with fixed values as well as some additional unknown parameters which consider, as an example, an influence of some external factors and which are to be determined separately.

• VI.    Solution of the equations solving the problem, analysis of the established relationship and transforming it to get the most convenient form for derivation of the measurement equation. In this case, two variants should be considered as follows: a) additional unknown parameters are represented as corrections provided they are empirically calculated in an independent way; b) the established relationship is used to formulate a set of equations that allows determining the quantity to be measured (the measurand) and some additional unknown parameters provided that they are instrumentally determined.

• VII.    Derivation of the measurement equation and estimation of methodical error (uncertainty) of the measurement result. Reducing the measurement equation to a standard form relating to direct, indirect, collective, joint or system measurements.

Let us consider a possible block diagram of the case of practical implementation of the above algorithm of the measurement equation justification [11 - 18] and estimation of the methodical error (uncertainty) of the measurement result for an exemplary indirect measuring. As before, we assume that there is only one unknown quantity value (while this algorithm is valid to another case with more than one quantity value, where the singular form of “quantity value” should be replaced by its respective plural form). The block diagram is given herein below, where the numbers denote actions, and the Roman letters signify the conditions of execution of these actions, namely:

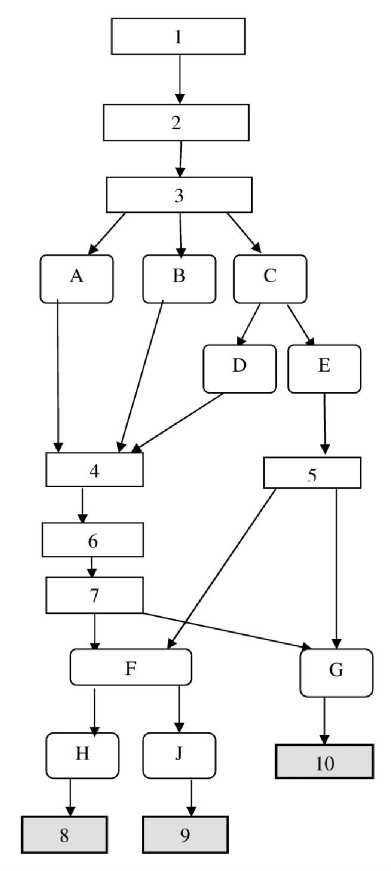
Figure 1. Block diagram of the case of practical implementation of the above algorithm of the measurement equation justification.

• 1    – identifying of the measurement object, the quantity to be measured and the values to be measured immediately;

• 2    - listing of effects that are essential for the formation of the functional relationship between the quantity to be measured and the values to be immediately measured;

• 3    - based on an analysis of the literature on the subject, availability for relations connecting the immediately measured quantity values and the quantity to be measured (and their accuracy evaluation) should be defined;

• 4    – formulating of the equations for the physical effects and processes with their initial and boundary conditions that reflect the measurement problem specificity (mathematical formulation of the problem) ;

• 5    – using of the relations already available in the literature on the subject for justification of the equation of measurement, and the estimation of their accuracy should be applied to the evaluation of the methodical error (uncertainty) in the measurement;

• 6    – completing an analysis and an assessment of contributions of the individual physical effects and processes to the formation of the relationship between the desired quantity to be measured and the immediately measured quantity values, specifying the list of the effects and simplifying the original problem statement;

• 7    - solving the problem and obtaining the relations between the quantity to be measured and the immediately measured quantity values. Assessing of accuracy of the obtained relations on the basis of an analysis of the simplifications made before, when formulating and solving the problem;

• 8    - formulating of a set of equations necessary for determination of additional unknown parameters and the desired quantity to be measured with the obtained relations, which are presented for various values of the recorded parameters and the corresponding immediately measured quantity values (for the same values of the quantities to be determined as well as

additional unknown parameters). Finding the equation of the measurement as a result from solving the above set of equations. Assessing of the methodical error based on the evaluation of the accuracy of the relations, as given above, which describe the relation between the desired quantity to be measured and the immediately measured quantity values;

• 9    – obtaining of the measurement equation using the derived relations where the additional unknown parameters, determined by computation, play the role of corrections. Methodical error should be estimated based on the assessment of the relation accuracy, as given above, which describe the relation between the desired quantity to be measured and the immediately measured quantity values, taking into account errors for establishing the corrections;

• 10 – transforming of the derived relations into the measurement equation. Utilization of the error caused by the inaccuracy of the relations as the methodical error of the measurement equation.

A – relations are not available;

B - relations are available, but without estimation of accuracy;

C - relations are available with estimation of accuracy;

D - accuracy does not comply with the specified requirements;

E - accuracy complies with the specified requirements;

F – the obtained relations contain not only the known constants, the recorded parameters, the desired quantity to be measured and the immediately measured quantity values, but also some additional unknown parameters (taking into account, for example, external environment influence), which should be determined separately;

G - the derived relations contain the known constants, the recorded parameters, the desired quantity to be measured and the immediately measured quantity values only;

H - additional unknown parameters are determined with instrumentation;

J - additional unknown parameters are determined by calculation using supplementary data.

From the above algorithm description, it follows that in those cases when the relevant data are available in the literature, some steps of the algorithm may be skipped. Among the other things, it should be noted that the wording used to define the actions prescribed by the algorithm cannot be considered in isolation from the wording describing the conditions of execution of these actions.

Conclusions

The review and the critical analysis of the literature dedicated to the solution of the problem of justification for the equation of measurement and the estimation of the methodical error (uncertainty) of the measurement result have been conducted herein. It has been shown that the mathematical formulation of the problem within the context of the approach presented in [11 - 18] is based on the application of rigorous formulations of physical laws (laws of nature) with the relevant boundary and initial conditions, considering the specificity of the given measurement task. The algorithm proposed in the present paper can be utilized for derivation of the measurement equations necessary for the development of new measurement methods, as well as for the development of measuring instruments to implement such methods, including analysis of the measurement result accuracy.

Statement on ethical issues

Research involving people and/or animals is in full compliance with current national and international ethical standards.

Conflict of interest

None declared.

Author contributions

The author read the ICMJE criteria for authorship. The author read and approved the final manuscript.