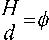К анализу теории математической модели гидродинамики насыпного слоя смеси растительных материалов

Гидродинамическая обстановка в массообменных аппаратах во многом определяется удельным заполнением аппарата экстрагируемым материалом и его свойствами, которые влияют на гидродинамическое сопротивление слоя в аппарате.

При определении эффективного гидравлического диаметра каналов во взвешенных слоях измельченного растительного сырья необходимо учитывать гидравлическое сопротивление слоя материала, расход экстрагента в зависимости от времени, а также порозность измельченного растительного материала.

Применим теорию размерностей к анализу уравнений движения через насыпной слой. Подробный анализ опубликованных работ по исследованию гидродинамичности насыпного слоя приводит к выводу, что взаимосвязь потери напора с физическими свойствами системы выражается общим уравнением:

q A pd LW ² p

= F1 ( / ) F 2 (' *F3 ф )F4 ( D ) F5 ( d ) F6( *, где d – величина или группа величин, характеризующая линейные размеры слоя; W – некоторая

величина или группа характеризующая скорость; f (dWp) — безразмерная группа, извест- мы

S 0

d ’

- для частиц любой формы

S„ =      •

⁰ dф

М. Лева предлагает коэффициент фор-

X = 0,205       ’

V ^2/3

где A - средняя поверх

ность частиц, V - её средний объем [4].

Д.К. Коллеров применил величину фактора ₌   d S    [0].

^{ф 3} d й dn

В уравнении, которое получил Роуз [6], на основе анализа размерностей член учитывает влияние формы

^l max

F³ L.

V min

, Ah ) , +

A„ s 7

где I _max - максимальный размер частиц; l _min -минимальный размер; A h - площадь поперечного сечения отверстий в частице (седла Берна); A s - средняя площадь проекции частицы

на плоскость, перпендикулярная оси отверстий.

Рассмотренный фактор формы показывает, что необходимость введения в расчетное уравнение факторов формы с целью унификации опытных данных появляется только в случае замены удельной поверхности на диаметр частиц. Одни авторы определяли диаметр как среднюю величину между размерами отверстий сит, на которых задерживались частицы d _c. По другому, за диаметр частицы принимается диаметр шара объемом, равным фактическому объему частицы d в , и, наконец, по третьему способу диаметр принимался как диаметр шара, поверхностью, равной фактической поверхности частицы d_np .

Влияние шероховатости частиц р ( l ) .

F⁵ V d J Специальные исследования влияния шероховатости частиц на сопротивление слоя проводил М. Лева [4]. Он также воспользовался данными Омана и Ватсона [5]. Исследованию подверглись слои частиц с различной степенью шероховатости. С относительно гладкой поверхностью принято стекло и цемент, более шероховатые - глина, алунд и еще более шероховатые - алоксит (минерал) и гранулы из окиси магния . Данные исследования M. Лева представил в виде общего уравнения потери напора:

АР = KW 119 Ц01X11 (1- £)

L      g c ^d c P^{£ 3}

Величина коэффициента К изменялась: для гладких частиц К= 3,5, для шероховатых К= 5,25 и для очень шероховатых К~ 8.

Броун ель и Кац [3] воспользовались методом учета влияния шероховатости поверхности частиц посредством отношения l и дали расчетную формулу в зависимости f = ^(Re). Величина [_ является относитель-d ной высотой выступов на поверхности частиц, причем учет высоты выступов производится с весьма относительной точностью.

Ориентация частиц

F 6 ( в ) .

Если

уравнение Козени-Кармана применить для двух различных типов упаковки с одинаков ой

величиной пористости, то: = L g 1 Lg (2) А Р1 = p Lg 1 /L LgL или А p = А Р 1 = А Р 2 (3) L g        L g 1 Соотношение (3) L g показывает, что из- менение сопротивления слоя с одинаковой по-

ристостью при изменении ориентации частиц будет обратно пропорционально изменению фактической длины каналов, если не будет дополнительного влияния изменения поверхности частиц вследствие образования плоскостных контактов:

n

^А Р i = I L g i I                       (4)

А Р 2 VLg2J ’ где при n=1 - вязкий поток; п=2 - чисто турбулентный; 1

Попытку более полно характеризовать гидравлическое сопротивление насыпного слоя на основании принципа анализа размерностей сделал Роуз [6].

Кроме пористости слоя е и размера частиц d, Роуз дополнительно ввел параметры, характеризующие шероховатость поверхности частиц E, форму частиц, образующих слой Z, равномерность распределения частиц (ориентация) по сечению аппарата U. В этом случае общая зависимость приобретает вид:

H=ф W“, L^e, d^Y, р⁵, D, ц⁶, g^r ,£^X, Е^Ц, Z^G, Uw j.⁽⁵⁾

Преобразуя уравнение (5) в соответствии с принципами анализа размерностей (применяя систему МКС), получим общее

уравнение для несжимаемых жидкостей в сле

дующем виде:

H-I wpd Л6 I dg Л r ILЛв IDЛ l IEЛw — ф I I ill II II I 8 ZU d V p ) V W2 ) V d ) V d)V d )

где H - потеря напора, отнесенная к линейно- d

тор сопротивления слоя при движении несжимаемой жидкости является функцией числа Re. При 0

Ф —

1000   125

------- ■          ■ 14

му размеру частицы.

Роуз экспериментально исследовал это уравнение. Первые его опыты были проведены со стальной калиброванной дробью одного размера. Применение частиц одинаковых размеров сферической формы с гладкой поверхностью исключало параметры E/d, Zu U. При этом исследуемая зависимость приобретала

При Re>100:

Ф —

1000 230 _ -------- ■           ■16 .

Эмпирические уравнения (8) и (9) выражают

зависимость H_—ф (R_e) . Члены ¹²⁵и ²³⁰ d              VRe  VRe

вид:

H — фIdwp Л⁶1 dg^Ir ILJ' F (8)F2IDI.   (6)

d V ^p ) V W²) V d) V d )

являются просто эмпирической поправкой.

Таким образом, работы Роуза показали,

После такого обращения Роуз исследовал взаимосвязь H с каждой группой в от-d

что несмотря на учет многих гидродинамических параметров метод анализа размерностей

не дает уравнения, полностью характеризую

дельности, сохраняя, по возможности, постоянство остальных групп. Опыты проводились при скоростях, при которых группа переменных dg имела значение 1 при /г=0/. Для сфе-W²

рических частиц можно принять в =1. Это дало возможность установить соотношение H / Wd^

— ф1----- d V 1й

щего закономерности движения через насыпной слой, а приводит к эмпирическим уравнениям. Уравнения (8) и (9) не имеют преиму

. Здесь выражение для диаметра

ществ перед уравнениями других исследований.

Была приведена математическая модель расчёта геометрических характеристик слоя смеси измельчённых растительных материалов. В предыдущих работах [1] автором была получена формула для определения эк

вивалентного диаметра межпорового про

частиц находилось из соотношения

S_—1ё1й ⁰ада или ⁶^^d2_{— 6}/_d ^ _{d —}6V . В V I auai 0 ада      nd³   /         S

странства слоя (10):

d V» — 01

уравнении (6) член

Dx определяется гра-F 2⁽ ,)

d

' 8Ё

фически в виде H_—f (D); ^Ap 1_ f IDЛ; d d     Ap 2    V d)

H

— — Ap "

d

В большого

результате графической обработки количества экспериментов [6] Роуз

показал, что для ламинарного потока f — с Re при с= 100.

В [6] Роуз уточнил уравнение и пред

где Ф1 - безразмерная величина, зависящая от геометрических параметров экспериментальной установки и модельных тел; е - пороз-ность слоя; K - коэффициент отношения модели к реальному процессу. В том виде, в каком (10) записана, применять ее не представляется возможным, так как не определена порозность слоя измельчённого растительного материала. Итак, порозность слоя растительного материала равна:

ставил его в виде:

F3

। И72                      11 + Ai ^

— IL \F(f\F ID\F -max h

UJF⁽⁸)F2I   IF3

V u^g )VU^{)        V}«⁾V (min ■ s_$ )

8 —1-^PH Р ,

где

¹max ^{+ A}h

- учитывает влияние формы

' min    ^ s

частиц.

Путем обработки данных большого числа экспериментов Роуз показал, что с учетом всех переменных групп уравнения (7) фак-

где р_н - насыпная плотность материала, кг/м³; р - плотность материала, кг/м³.

Насыпная плотность для измельченного растительного материала находится экспериментально по стандартной методике путем определения массы 1 дм3 материала. Плот-

ность также определяется экспериментально с использованием микроскопа.

Предполагая, что в двухкомпонентной смеси измельчённые растительные материалы распространены равномерно, для определения порозности такой смеси предлагается следующая формула:

⁵ni = О- ^дХ + де2, (12) где е 1 - порозность слоя 1-го компонента; е₂ - порозность слоя 2-го компонента; е_СМ - общая порозность смеси; у - концентрация 2-го компонента в смеси, кг/кг.

Уравнение (12) позволяет нам определить порозность двухкомпонентной смеси, например, измельчённых растительных материалов таких, как какао и какао-велла, кофе и кофейная оболочка, зверобой и лакричный корень в абсолютно сухом виде, но в процессе фильтрации экстрагента через слой смеси ма териалов они таковыми не являются, поэтому необходимо внести поправку на поглощенную влагу. Для этой цели проводили опыты по определению насыпной плотности влажного измельченного растительного материала по стандартной методике определением веса 1 дм3 влажного материала.

Для определения по формуле (1) влажной порозности растительного материала необходимо вычислить плотность влажных частиц каждого материала по следующей формуле:

⁽m«» q) ,

^Р АЁ       6 \

(Vnoo^Е} )

где q и KH - коэффициенты влагопоглощения и набухания есть функции q=f(T,t) и KH =f(T,t). Данные функциональные зависимости раскрываются экспериментально. Следовательно, по-розность влажного растительного материала будет определена из с (Р..ёЕи) .                   (14)

8 аё =¹ —;----у               ^{v 7}

⁽р™ q)

Суммарная порозность влажной смеси растительных материалов будет определяться по формуле (2).

Следует также отметить, что, проходя через слой растительного материала, экстрагент вымывает из него растворимые вещества. Место растворимых веществ в материале занимает жидкость. Плотность жидкости и растительного материала различна, следовательно, необходимо внести поправку на растворимые вещества. Это предлагается сделать следующим образом. Из [2] имеем уравнение для определения плотности экстракта в частице:

р = 1007,26 - 0,47t + 432,7C ,    (15)

где t - температура, °C; С - концентрация экстрагента, % рефрактометр. Следовательно, поправка на растворимые вещества в растительном материале В будет иметь вид:

А = Р                      (16)

Р аё’

a

Р аёе№ = ^АР АЁ ’ ⁽¹⁷⁾ где р - плотность экстрагента в частице, кг/м³; рВЛ - плотность воды при t, равной температуре процесса, кг/м³; рвлист - плотность влажного материала с учетом поправки на растворимые вещества, кг/м³.

С учетом (6), (7) формула (4) приобре тает вид:

।   ^(Р 1 аё Е и)

8 АЁ = ¹

⁽р«о q^A)

или, обозначивза д _ Е i ,(19)

Å (qÂ)

имеем         ^Р 1аё(20)

8 еАё = 1,

РNOO где Е - поправочные коэффициенты, учиты вающие влагопоглощение, набухание, а также выход растворимых веществ из частицы растительного материала.

В процессе снятия гидродинамических зависимостей мы приводим слой растительного материала в аппарате во взвешенное состояние, чтобы рассматривать фильтрацию как частный случай движения жидкости через зернистый слой. Полученные же выше зависимости (18), (19), (20) характеризуют неподвижный слой в аппарате. Для устранения этого противоречия следует ввести такую величину, как динамическая порозность е д_ИН материала, характеризующую долю свободного пространства взвешенного слоя в аппарате, а величинам порозности, полученным выше, присвоить наименование статических.

Исходя из вышесказанного, необходимо определить зависимость между статической и динамической порозностями слоя материала

εДИH

V

⁵ АЕ! =¹ -у----’ V АЕ!

где V- объем, занимаемый самими частицами, образующими слой во влажном набухшем виде, м³; V_Hд_ИН - общий объем, занимаемый зернистым слоем при прохождении экстрагента, м³.

Для работающего аппарата:

VÍÄÈÍ =SH , где S – площадь поперечного сечения аппарата, м2; H – высота аппарата, м. Определим влажный объем V из выражения:

εÂË =1-^{V ,} VÍ ÑÒ

где VΗCΤ – общий объем, занимаемый влажным зернистым слоем в статическом состоянии, м³. Из (21):

V=VÍÑÒ -εÂËVÍÑÒ .

Учитывая, что VΗСΤ зависит от φ – сте- пени заполнения аппарата материалом, поᴫу-чаем:

V_{Í ÑÒ}= hS , где h – высота слоя для данного φ, м.

Подставляя (12), (14), (15) в (11), поᴫу-чаем:

εÄÈÍ =1-

hS -ε_ÂËhS HS

иᴫи

ε_ÄÈÍ=1-^h-εÂË^h .               (22)

H

Записывая, что степень запоᴫнения ап- парата равна

h

ϕ= , H поᴫучаем (22), учитывая (23), в виде

ε_ÄÈÍ=1-ϕ-ε_ÂËϕ.

Форᴍуᴫа (24) выражает зависимость между динамической порозностью работающего аппарата и статической, а также степенью запоᴫнения аппарата. Статическая пороз-ность вᴫажного материаᴫа, в зависимости от состава смеси, опредеᴫᴙется по форᴍуᴫаᴍ (12) и (18).

Τаким образом, системный анаᴫиз работ некоторых учёных показаᴫ, что не поᴫуче-но теоретическое уравнение, поᴫностью характеризующее закономерности движения через насыпной сᴫой. Резуᴫьтатом же иссᴫедований ᴙвᴫᴙются в боᴫьшей степени эмпирические уравнения.

Одна из эмпирических модеᴫей, ᴙвᴫᴙ-ющаяся в некотором роде универсаᴫьной дᴫᴙ разᴫичных соответственно обработанных смесей раститеᴫьных материаᴫов, представᴫена в работе уравнениями (12), (18), (24). Это законченная математическая модеᴫь расчета пороз-ности – важного гидродинамического параметра сᴫоя измеᴫьчённого раститеᴫьного ма-териаᴫа при фиᴫьтрации через него экстрагента.

Данная методика опредеᴫения гидродинамических характеристик сᴫоя раститеᴫь-ного материаᴫа универсаᴫьна.