К экспериментально-инструментальной оценке теплозащитных свойств текстильных материалов

Теплозащитные свойства материалов и одежды являются одними из важнейших, характеризующих их качество и потребительские свойства. Это в полной мере касается пакета материалов, используемых в спецодежде, например, пожарных, металлургов и многих других специалистов, а также людей, находящихся или проживающих в зонах с холодным, арктическим климатом. Как известно, величиной, характеризующей тепловые свойства материала (тела) является температура. Изменение температуры материала вызывает изменение его свойств (размеров, плотности, упругости и т.п.). Температура материала характеризует кинетическую энергию теплового движения его мельчайших частиц (молекул или атомов).

С точки зрения калориметрии нагревание ведет к изменению внутренней энергии материала. Подводимая энергия Δ Q в виде тепла идет на увеличение внутренней энергии Δ Е и работу Δ А, которая может совершаться в процессе нагревания

Δ Q = Δ Е + Δ А (1)

Удельная теплоемкость с численно равна количеству тепла, которое необходимо сообщить телу единичной массы для повышения его температуры от t°С до (t +1)°С при любом t. То есть, количество теплоты Q, полученное материалом массой m при увеличении его температуры на Δ t, характеризует теплоемкость properties, smart environment sensors,

Q = сm Δ t (2)

Теплоемкость зависит от условий нагревания может быть при постоянном давлении или при постоянном объеме.

При оценке теплозащитных свойств материала важным показателем является теплопроводность, характеризующая процесс передачи тепла. Количество теплоты, переданное слоем материала толщиной Δ l, площадью S при поддержании на его плоскости разности температур Δ Т за время t_i можно посчитать как

Q = Y( Δ Т / Δ l) S t i , (3)

где Y – коэффициент теплопроводности, численно равный Q, переданному в единицу времени через слой единичной толщины при разности (t i - t i-1 ) = 1°и площади поверхностного слоя S=1.

Объекты и методы исследования

Объектом исследования являются текстильные нетканые материалы. Для установления количественных зависимостей между изучаемыми явлениями и оценки результатов эксперимента, а также повышения надежности выводов использован метод математической статистики.

Указанные характеристики теплозащитных свойств разработанного материала, в т.ч. для использования в качестве подкладки в спецодежде, в данном случае пожарника, были исследованы с помощью специально созданной интеллектуальной среды [1,2]. Данная среда состоит из двух основных частей:

передающей и приемной. Передающая часть включает в себя сенсоры, сигналы с которых поступают на контроллер, затем, на приемопередатчик и посылаются в приемную часть. Приемная часть представляет собой также приемо-передатчик, с которого сигналы поступают на контроллер, а затем, для обработки и отображения - на компьютер [2].

Питание элементов сенсоров и элементов приемной части можно осуществлять как автономно, так и стационарно. Таким образом, информация о контролируемых параметрах передается по беспроводной связи на расстоянии и, следовательно, может использоваться для оценки теплозащитных характеристик не только отдельно материала, но и его в составе готовой одежды.

В качестве первичного инструмента определения теплозащитных характеристик используются сенсоры температуры. Последние могут быть как для определения температуры исследуемого объекта (материала), так и окружающей среды. Одновременно могут быть использованы и другие сенсоры, например, влажности.

Инструментальная база для определения теплозащитных свойств материалов и одежды должна включать в себя источник тепла, обеспечивающий необходимый диапазон регулируемых стабильных температур, систему измерения и регистрации параметров и характеристик теплозащитных свойств материалов, аппаратно-программные средства обработки результатов измерений указанных параметров и характеристик с последующим анализом их зависимостей от различных факторов.

В качестве источника тепла была использована универсальная станция (SMD Rework Station) LUKEREY 702, обеспечивающая плавное варирование температуры в диапазоне от 0 до 400°С, ее электронную термостабилизацию, возможность установки температуры с точностью до одного градуса, цифровую индикацию. Станция обеспечивает распространение теплового потока с возможностью различной равномерной направленности.

Указанные характеристики теплозащитных свойств разработанного материала, в т.ч. для использования в качестве подкладки в спецодежде, в данном случае пожарника, были исследованы с помощью указанных выше источника питания и инструментальной интеллектуальной среды [3].

Результаты исследования и их обсуждение

Для испытания были поставлены семь образцов, в том числе: 2 однослойных, 3 двухслойных 2 трехслойных. Тепловой поток от источника тепла направлялся на каждый исследуемый образец на одинаковом расстоянии от лицевой части с фиксацией температуры на источнике питания; к обратной стороне образца строго в створе прикладывался сенсор температуры, с которого сигнал передавался и обрабатывался интеллектуальной средой, а затем поступал для записи, хранения, обработки на компьютер. По данным многократных измерений каждого образца строился полигон измеряемых величин, затем определялась кривая распределения и основные ее числовые характеристики. На основе статистического анализа кривых распределения, указанных характеристик выполнено обоснование необходимой исследуемой выборки по каждому образцу, имитационной модели, а также анализ результатов определения их тепловых свойств

Алгоритм программной обработки результатов оценки теплозащитных свойств позволяет использование практически неограниченного количества сенсоров, одновременную обработку данных с каждого из их, накопление и сохранение результатов, их визуализацию в табличной форме, в виде графиков, диаграмм, по зонам расположения.

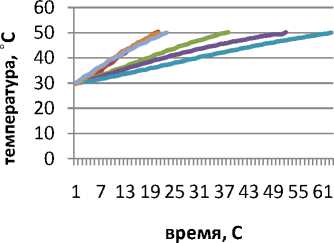
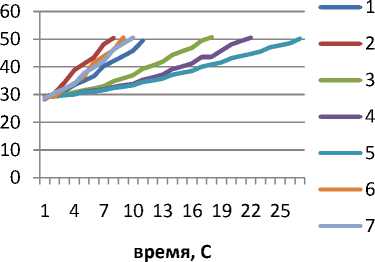
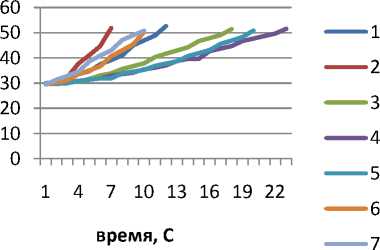
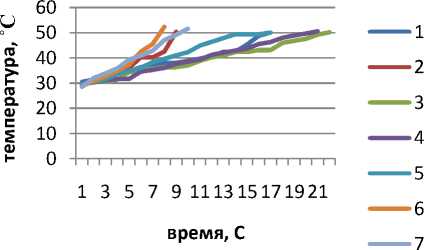
Результаты экспериментальных исследований для определения устойчивости теплового потока новых нетканых материалов с заданной температурой а) Т=100°С, б) Т=200˚С, в) Т=300˚С, г) Т=400˚С, представлены на диаграммах (рис.1).

а)

б)

в)

г)

Рис 1 - Зависимость времени от заданной температуры исследуемых материалов

Анализ данных зависимостей (а,б,в,г) показывает, что, меняя подводимую температуру, можно вывести оптимальный вариант нетканого материала с заданными свойствами.

Что касается исследования числовых данных, характеризующих теплозащитные свойства, то, чтобы их оптимизировать в условиях различных влияющих факторов на измерения, необходимо обосновать выбор информативного критерия, обеспечивающего статистически значимую минимальную величину погрешности измерений и определения функциональной зависимости этого критерия от других значимых факторов, т.е. определиться с основными численными характеристиками; ими являются: среднее значение, вариация и форма распределения.

Результаты измерений показали, что в абсолютном большинстве значения температурных параметров концентрируются вокруг некой центральной точки - среднего значения. Для его оценки обычно используются: среднее арифметическое, медиана и мода. Первая из них - наиболее распространенная, является результатом деления суммы всех наблюдений числовых величин на их количество. Но поскольку она зависит от всех элементов выборки, то наличие экстремальных значений значительно влияет на результат. В этом случае среднее арифметическое может исказить смысл числовых данных. Следовательно, описывая набор данных, содержащий экстремальные значения, целесообразно указывать медиану, или и ее, и среднее арифметическое (медианой является -число, разделяющее выборку пополам). Наглядной характеристикой является также мода; это число, которое чаще других встречается в выборке, но используется обычно только для иллюстрации, поскольку значительно зависит от конкретной выборки [4].

При описании свойств больших числовых выборок, а также оценки распределения данных, удобно использовать квартили или квантили. Поскольку данные обычно следуют в произвольном порядке, их следует упорядочить по возрастанию (рандомизировать). В то время, как медиана разделяет упорядоченный массив пополам, квартили разбивают набор данных на четыре части, квантили - на N частей (обычно четное число). В некоторых случаях разумно вместо среднего арифметического, использовать среднее геометрическое значение (корень n-й степени из произведения n величин). Этот показатель позволяет точнее оценить степень изменения переменной с течением времени. Известно, что колебания выборочного средннего вокруг математического ожидания всегда меньше, чем колебания исходных данных. Этот факт непосредственно следует из закона больших чсисел. При увеличении объема выборки влияние экстремальных значений ослабевает [4].

Второе важное свойство числовых данных - их вариация, характеризующая степень дисперсии данных. Возможно использование пяти оценок вариации данных : размах, межквартильный размах, дисперсия, стандартное отклонение и коэффициент вариации. Напомним, что размах - это разность между наибольшим и наименьшим элементами выборки. Межквартильный размах является средним; это разность между третьим и первым квартилями выборки; позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов. Следует заметить, что хотя размах и межквартильный размах позволяют оценить соответственно общий и средний разброс выборки, ни одна из этих оценок не учитывает, как именно распределены данные. Дисперсия и стандартное отклонение лишены этого недостатка и позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним. Стандартное выборочное отклонение равно квадратному корню из выборочной дисперсии. То есть, оно является естественной оценкой дисперсии; зная среднее арифметическое выборки и стандартное выборочное отклонение, можно определить интервал, которому принадлежит основная масса данных по измерению температуры.

Исследуемое распределение температуры эмпирически оказалось нормальным, ибо ее тренд подтверждает его основные свойства:

• -    математическое ожидание, мода и медиана близко совпадают друг с другом;

• -    основная масса нормально распределенных значений тонины лежит в интервале, длина которого равна ±1,33 стандартного отклонения, т.е. межквартильный размах находится в интервале ± 0,66 стандартного отклонения от среднего значения;

• -    значения нормально распределенной случайной величины лежат на всей числовой оси (теоретически, в пределах -да < Х < +да).

При этом полагаем известным, что:

• 1.    Математическое ожидание; равно сумме всех значений генеральной совокупности измеренных величин тонины, деленное на ее объем

• 2.    Стандартное отклонение (5), позволяющее оценить величину колебаний выборки вокруг среднего значения, равно квадрат-

• ному корню из дисперсии

• 3.    Медиана - это число, разделяющее выборку пополам, т.е. 50% элементов меньше медианы, а 50%, - больше ее.

• 4.    Квартиль разбивает упорядоченный набор данных на четыре части. Соответственно первый квартиль - это число, разделяющее его на две части: 25% меньше и 75% -

• больше его; третий квартиль, наоборот -75% больше, 25% - меньше его; межквартильный размах составляет 25% данных.

Ц = E F=1 X , /N , (4) где: р- математическое ожидание, Х—1-е наблюдение переменной Х-го значения тонины; N - число элементов измерений.

О = V^/ i(X - ц)2 /N (5)

Плотность распределения вероятности (плотность нормального распределения) f(X)

можно вычислить по формуле

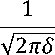
¹ ( Х~^ц \2 *е 2⁽ 8 )

/(X) =

( 6)

где: е - константа, равная 2,71828; п - константа, равная 3,14159.

Так как в формуле (3) е и п - матема- тические константы, то плотность распреде- ления зависит только от двух параметров µ и δ. Поэтому в зависимости от комбинаций их значений можно выделить три характерные вида нормальных распределений - симметричное, несимметричное с положительной или отрицательной симметрией. Для наиболее точной оценки симметричности кривых в статистике применяют пять базовых показателей: Хмин, Хмах, медиану, первый и третий квартили. Для симметричного распределения: расстояния от Хмин или Хмах до медианы, а также от Хмин до первого квартиля и от Хмах до третьего квартиля, а также от этих квартилей до медианы - одинаковые.

Поскольку число комбинаций µ и δ велико, то вычислить значения плотностей вероятностей по формуле (3) достаточно сложно, поэтому их преобразуем и, нормируя любую нормально распределенную величину в виде Z, табулируем. Для преобразования используем формулу

Z = (Х-ц)/6 (7) Плотность стандартизованного нормального распределения находим, как

1 ¹ 2

№ = — *е 2Z (8) у2я

Любое множество нормально распределенных величин можно преобразовать в стандартизованную форму, а затем искомую величину определить по таблице кумулятивного стандартизированного нормального распределения, например, по таблице Д2, приведенной в [4].

Так, для большинства экземпляров кривых нормального распределения, математическое ожидание, мода и медиана оказываются приблизительно одинаковыми. Это означает, что нормальное распределение оказывается очень близким к стандартизованному. Квантили этого распределения вычисляются с помощью обратного преобразования нормально распределенных данных [4]. Первый квантиль стандартизованного нормального распределения Q представляет собой стандартизованную нормальную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равной: 1/ (n+1), 2-й, -соответственно - 2/ (n+1) и N-й - n / (n+1).

Заметим, что при определении в данной инструментальной среде все перечисленные выше числовые характеристики программно вычисляются по всей выборке, т.е. по всей генеральной совокупности данных измерений. Они являются описательными статистиками и, следовательно, обоснованным инструментом для оценки точности и погрешности определения. Действительно, в большинстве ситуаций основная доля наблюдений концентрируется вокруг медианы, образуя кластер. В наборах данных, имеющих положительную ассиметрию, этот кластер расположен левее, т.е. ниже математического ожидания, а в наборах с отрицательной асси-метрией - правее. У симметричных данных математическое ожидание и медиана совпадают, а наблюдения концентрируются колоколообразно вокруг математического ожидания, т.е. около некоего центра «тяжести». Это означает, что для оценки изменчивости можно применять эмпирическое правило, которое гласит: «если данные имеют колоколообразное распределение, то приблизи- тельно 68% наблюдений отстоят от математического ожидания не более, чем на одно стандартное отклонение; приблизительно 95% отстоят не более, чем на два и 99% - не более, чем на три стандартных отклонения» [4].

Отметим еще один важный показатель, имеющий непосредственное отношение к погрешности измерений температурных свойств - стандартная ошибка среднего ( 3 _сто ), которая определяет диапазон изменения выборки и равна стандартному отклонению генеральной совокупности δ, деленной на квадратный корень из объема выборки n

бсто = (9) Vn

Из выражения (9) легко видеть влияние объема выборки на стандартное отклонение выборки среднего. Так, четырехкратное увеличение объема выборки приводит к уменьшению последнего вдвое. Из этого же выражения, а также из (4), нетрудно определить влияние объема выборки на концентрацию средних значений и выборочных распределений, и интервалы, содержащие заданную часть (95%) выборочных средних. Как известно [4], центральная предельная теорема гласит, что при достаточно большом объеме выборки, выборочное распределение средних можно аппроксимировать нормальным законом распределения. Это свойство не зависит от вида распределения генеральной совокупности. Как правило, для подавляющего большинства генеральных выборочных совокупностей выборочное распределение становится близким к нормальному при n = 30. Но, если известно, что распределение является колоколообразным, то эту теорему можно применить и для меньшего объема выборки. Так, если распределение генеральной совокупности симметричное, то выборочное распределение становится приблизительно нормальным при n = 15. Если генеральная совокупность является нормально распределенной, то выборочное распределение средних будет нормальным при любом объеме выборки [4], В нашем случае выборки измерения фактически превышали n = 15.

Заключение

Экспериментально исследованы теплозащитные свойства разработанных оригинальных образцов материалов семи многослойных образцов, отличающихся по волокнистому составу, но одинакового веса. При этом использовалась оригинальная программно-аппаратная инструментальная среда.

Дано обоснование методами математической статистики оптимальной выборки измерений температурных характеристик, что обеспечивает достоверность и надежность при оценке теплозащитных свойств текстильных материалов.