К оценке времени загрузки web-страницы сайта дистанционного обучения

Использование Web-технологий все более активно и масштабно проникает во все сферы человеческой деятельности: науку, технику, электронную коммерцию, образование. Причем, на качественные, экономические и другие показатели Web-сайтов в значительной мере влияет их время загрузки, которое при условии использования равноценных компьютерных средств, во многом зависит от конструкции Web-сайта, текущего трафика.

Исследования ряда разработанных Web-сайтов, предназначенных для использования при дистанционном обучении в АТУ [1], показали, что среднее время загрузки Web-страницы одного из них составило 7 с., а его dispersion, standard deviation, fashion, median, стандартное отклонение – 2 с.; размах загрузок – 12 с. Из общего числа загрузок, а их генеральные совокупности составляли не менее, чем по 60 ÷100 наблюдений, 95% колебалось в интервале от 2 до 11 с, а 66% - в диапазоне 5 – 9 с. Измерения времени загрузки Web-страниц проводились с помощью больших электронных часов с шагом 1 с.; погрешность измерений не превышала десятые доли секунды.

Чтобы построить кривую распределения времени загрузок, сначала были упорядочены наблюдения. Они откладывались по горизонтальной оси, а значения числа наблюдений – по вертикальной оси (рис.1).

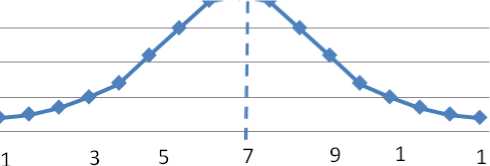
Рис. 1 - Время загрузки Web – страницы сайта №1.

t,сек.

Исследуемая форма распределения времени загрузок оказалась близкой к кривой Гаусса, т.е. приняла нормальный закон распределения. Создание затем упорядоченного ряда данных позволило найти соответствующие статистические показатели, в том числе вычислить квантили стандартизованного нормального распределения. Далее была проведена всесторонняя проверка гипотезы о нормальном распределении времени загрузки Web-страницы.

Объекты и методы исследования

Для оценки оптимальности конструкции Web-сайтов небезынтересно на основе полученной информации определить частоту времени загрузки Web-страницы, не превышающей определенное приемлемое время, и в каком интервале это время составит подавляющее большинство, допустим, - 99%, Обратимся к методам статистики.

Время загрузки Web-страницы является случайной величиной, причем численно – непрерывной, т.к. это время измеряется, а не подсчитывается. Математическим выражением, описывающим распределение таких величин, является плотность непрерывного распределения их вероятности. В общем случае такое распределение может быть нормальным, равномерным, экспоненциальным или иным. Как указано выше, исследуемое нами распределение времени загрузки Web-сайтов, эмпирически оказалось нормальным, ибо оно подтверждает его основные свойства:

• -    имеет колоколообразную форму;

• -    его математическое ожидание, мода и медиана совпадают друг с другом;

• -    основная масса нормально распределенных значений времени загрузки лежит в интервале, длина которого равна ±1,33 стандартного отклонения, т.е. межквартильный размах находится в интервале ± 0,66 стандартного отклонения от среднего значения;

• -    значения нормально распределенной случайной величины лежат на всей числовой оси (теоретически, в пределах -∞ ≤ Х ≤ +∞).

Результаты, их обсуждение

При этом полагаем известным, что:

• 1.    Математическое ожидание равно сумме всех значений генеральной совокупности измеренных величин загрузок, деленное на ее объем

• 2.    Стандартное отклонение δ, позволяющее оценить величину колебаний выборки вокруг среднего значения, равно квадратному корню из д исперсии

• 3.    Медиана – число, разделяющее выборку пополам, т.е. 50% элементов меньше медианы, а 50%, - больше ее.

• 4.    Квартиль разбивает упорядоченный набор данных на четыре части. Соответственно первый квартиль – это число, разделяющее его на две части: 25% меньше и 75% - больше его; третий квартиль, наоборот -75% больше, 25% -меньше его; межквартильный размах составляет 25% данных.

дг

#- = У(^)/лг,                (1)

Ё —1

где µ- математическое ожидание, Х i –i-е наблюдение переменной Х времени загрузки Web-страницы, N- число наблюдений.

' * (2)

Плотность распределения вероятности (плотность нормального распределения) /to можно вычислить по формуле

7(х) = -^= * е2' 6 , (3) <2га?

где: е – константа, равная 2,71828, π – константа, равная 3,14159.

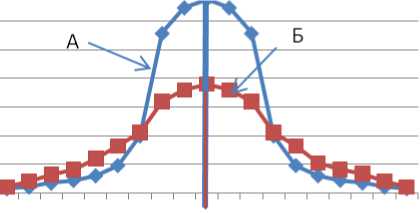
Так как в формуле (3) е и π – математические константы, то плотность распределения зависит только от двух параметров µ и δ. Эти параметры часто называют моментами, соответственно первым и вторым. Плотности нормального распределения времени загрузки для Web-страниц одного и того же сайта могут иметь одинаковые первые моменты, но разные – вторые, или наоборот – разные первые и одинаковые – вторые, или и те, и другие разные. Поэтому в зависимости от комбинаций значений µ и δ можно выделить характерные виды нормальных распределений, полученные для времени загрузки Web-страниц других исследованных сайтов (рис.2).

123456789 10111213141516171819

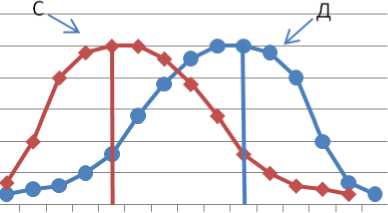
Рис. 2 - Кривые нормального распределения. (а – симметричное, б – несимметричное с положительной и отрицательной симметрией).

1 2 3 4 5 6 7 8 9 1011 12 13 1415

На рис. 2 показано, что распределения С и Д - несимметричные и характеризуются третьим моментом – коэффициентом ассиметрии, кривые А и Б – симметричные, но отличаются уплощением и характеризуются четвертым моментом – коэффициентом эксцесс. Для наиболее точной оценки симметричности кривых в статистике применяют пять базовых показателей: Х мин , Х мах , медиану, первый и третий квартили [2,3], для симметричного распределения: расстояния от Х мин или Х мах до медианы, от Х мин до первого квартиля и от Х мах до третьего квартиля, а также от этих квартилей до медианы - одинаковые. Поскольку число комбинаций µ и δ велико, то вычислить значения плотностей вероятностей по формуле (3) достаточно сложно, поэтому их преобразуют и, нормируя любую нормально распределенную величину в виде Z, табулируют. Для преобразования используют формулу

z = qc-^6 (4)

Плотность стандартизованного нормального распределения находим как

Любое множество нормально распределенных величин можно преобразовать в стандартизованную форму, а затем искомую величину вероятности определить по таблице кумулятивного стандартизированного нормального распределения, например, по таблице Д2, приведенной в [2]. Кривая Гаусса, построенная для генеральной совокупности по данным испытаний времени загрузки Web–сайта №1, как указано выше, имеет вид (рис 1) на ней µ = 7с., δ =2с. На шкале переменных этой зависимости Х укажем найденные по формулам (1,2) соответствующие значения µ ± δ, µ ± 2δ, µ ± 3δ. Им соответствуют значения µ, равные 1, 2, 3, 9, 11, 13. Далее по формуле (4) нанесем на шкале Z соответствующие значения; они равны: -3, -2, -1, 0, +1, +2, +3. Покажем это на рис.3.

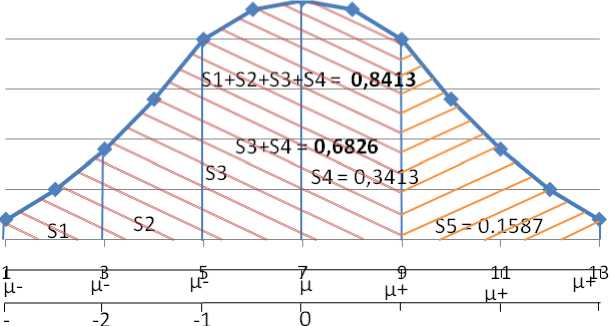
Рис.3 - Площадь фигуры, ограниченная интегральной кривой стандартизированного нормального распределения.

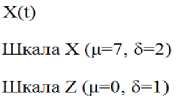
На нем каждому значению переменной Х соответствует нормированное значение Z, из чего следует, что время загрузки Web–страницы на одну единицу стандартного отклонения δ больше математического ожидания µ, это очевидно, так как Z = (9 – 7) / 2 = +1. Соответственно, время загрузки, отличающееся на 3δ, равно -3 (т.к. Z = (1 – 7) / 2 = -3) и значит меньше µ. Таким образом, для времени загрузки Web–страницы стандартное отклонение можно считать его единицей измерения .

На рис.3 показан полигон относительных частот, соответствующих времени загрузки одного сайта. Поскольку результаты измерений образуют полную генеральную совокупность вероятностей, сумма вероятностей, т.е. площадь фигуры под кривой, должна быть равной единице. Вернемся к нашей задаче определения вероятности того, что время загрузки Web– страницы не превышает определенное, например, 9с. Поскольку времени загрузки соответствует математическое ожидание, отличающееся на одно стандартное отклонение, то следует определить вероятность того, что время загрузки не превышает величину (µ + δ). Воспользуемся указанной выше таблицей Д2 [2] кумулятивной вероятности, т.е. площади фигур, ограниченных стандартизированной гауссовой кривой, и, лежащих левее величины Х, а по отношению к формуле (4) – левее Z.

Для наглядности покажем фрагмент этой наших исследованиях. Заметим, что обычно Z таблицы (табл. 1), ограничившись лишь записывается с двумя цифрами после запятой (в некоторыми значениями Z из таблицы Д2, нашем примере Z записывается как +1,00). используемых для дальнейших вычислений в

Таблица 1 - Площади фигур, ограниченные кривой нормального распределения.

Z	0.00	0.01	0.02	0.03	0.04	0.05.	0.06	0.07	0.08	0.09
0.0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5209	0.5239	0.5279	0.5319	0.4359
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.4	0.6554	0.6591	0.6628	0.5910	0.6664	0.6736	0.6772	0.6808	0.6884	0.6889
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7518	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8022	0.8054	0.8076	0.8106	0.5133
1.0	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8577	0.8599	0.8106	0.8621
••    •••     •••      •••      •••     •••     •••      •••      •••     •••     •••
-1.9	0.0287	0.0281	0.0274	0.0268	0.0262	0.0256	0.0259	0.0244	0.0239	0.0232
-1.7	0.0446	0.0436	0.0437	0.0418	0.0409	0.0401	0.0392	0.0384	0.0275	0.0267
-1.6	0.0549	0.0537	0.0526	0.0516	0.0505	0.0495	0.0485	0.0175	0.0465	0.0455
••    •••     •••      •••      •••     •••      •••     •••       •••     •••     •••
-1.2 \	0.1151	0.1112	0.0526	0.1075	0.1056	0.0495	0.1038	0.2031	0.1003	0.0985

Чтобы найти вероятность, значения Z = +1,00, необходимо просмотреть столбец Z таблицы 1 и найти строку, соответствующую первым двум цифрам Z. Такой строкой является та, в которой стоит значение Z, равное 1,0. Далее переместимся по этой строке и найдем значение, находящееся на пересечении со столбцом, соответствующим сотым долям величины Z; в нашем случае она равна 0, т.е. находится в первом столбце (0,00). Следовательно, искомая вероятность, находящаяся на пересечении соответствующих строки и столбца, равна 0,8413 и это означает, что Web– страница загружается меньше, чем за 9 с. и ее вероятность составляет 84,13%. Изложенное выше проиллюстрируем (рис.3), как время загрузки Web–страницы, определяемое площадью фигуры, ограниченной интегральной кривой стандартизированного распределения. Нетрудно определить вероятность того, что время загрузки рассмотренной Web–страницы превысит 9 с., как разность 1 – 0,8413 = 0.1587. Также просто определить вероятность того, что время загрузки Web–страницы лежит в определенном интервале, например, от 7 до 9 с. Для этого необходимо определить, что загрузка продлится более 7 с. и вычесть из уже известной вероятности того, что она составляет не более 9 с. Поскольку математическое ожидание и медиана нормального распределения совпадают, то вероятность превышения загрузки 7 с. из (4) следует Z = (7 - 7) / 2 = 0,00. По таблице 1 определяем, что площадь фигуры, ограниченной нормальной кривой и значением Z = 0,00, равна 0,05. Следовательно, площадь, лежащая под нормальной кривой между значением Z = 0,00 и Z = -1,00, равна 0,8413 – 0,5000 = 0,3413. Аналогично определяется из предыдущего случая вероятность того, что время загрузки Web–страницы лежит в интервале меньше 7 с. и больше 9 с., поскольку является противоположным событием, т.е. 1 – 0,3413 = 0.6587. Эта же оценка может быть сделана иначе, исходя из того, что вероятности событий Р(Х<7) и Р(Х>9) известные; сложим их и имеем 0,5000 + 0,1587 = 0,6587. Так же просто определить и вероятность того, что время загрузки лежит в пределах от 5 до 9 с., т.е. Р(5<Х<9). Для этого, учитывая, что формула преобразования (4) позволяет вычислить лишь вероятность того, что случайная величина меньше определенного значения µ, а в данном случае интервал времени загрузки лежит по разные стороны математического ожидания, используем следующий алгоритм решения: вначале вычислим вероятности Р (Х<9) и Р(Х<5), затем вычтем результат один из другого. Первый результат нам уже известен, т.е. когда время загрузки не превышает 9 с. и равно 0,8413, а, чтобы найти второй результат, вычислим по (4) значение Z = (5 - 7) / 2 = -1,00. Далее из таблицы 1 следует, что Z = -1,00 соответствует вероятность 0,1587. Тогда, окончательный результат равен 0,8413 – 0,1587 = 0,6826.Таким образом, воспользовавшись формулой (4) и таблицей 1 (в общем случае Д2[2]), можно определить, что площадь S, расположенная под нормальной кривой и ограниченная значениями Х и соответственно Z, равна:

• -    при Х=3, Z = -2,00 S = 0,0228;

• -    при Х=1, Z = -3,00 S = 0,0135;

• -    при Х=11, Z = +2,00 S = 0,9772;

• -    при Х=13, Z = +3,00 S = 0,9986.

Полученные результаты хорошо согласуются с правилом Бьенами - Чебышева и эмпирическими правилами, которые, как известно [2,3], определяют число данных, лежащих вокруг математического ожидания и гласят, что процент данных, находящихся в интервале, составляет:

Интервал	Правило Бьенами-Чебышева	Эмпирическое правило
(µ - δ; µ + δ)	Минимум 0%	Приблизительно 68%
(µ - δ; µ + 2δ)	Минимум 75%	Приблизительно 95%
(µ - 3δ; µ + 3δ)	Минимум 88,89%	Приблизительно 99,7%

В нашем случае, при условии соблюдения правила 1δ, указанная вероятность составила 68,26,%; правила 2δ - несколько больше, чем 95% (95,44 %): и 3δ - 99.73%. Это значит, что для рассматриваемого сайта время загрузки Web–страницы, при условии соблюдения 1δ, лежит в пределах от 5 до 9 с,: 2δ - от 3 до 11 с, а при 3δ - в интервале от 1 до 13с. Выше мы рассмотрели случаи определения вероятности времени загрузки Web–страницы в определенном интервале. Небезынтересно, пользуясь формулой (4) и таблицей 1, решить «обратную» задачу - нахождение значений Х, соответствующих заданной интегральной вероятности. Воспользуемся следующим алгоритмом:

• -    построим гауссову кривую и отложим на ней математическое ожидание по шкале переменных Х и Z. При этом используем

выражение

X=μ+Zδ                         (5)

Его легко найти из (4), т.к. Z = (Х - µ) /δ, Z*δ = Х - µ, Х = Z*δ + µ. Далее:

• -    вычислим суммарную площадь фигуры, ограниченной нормальной кривой и лежащей слева от значения Х;

• -    используя таблицу 1, определим Z, соответствующую найденной площади;

• -    с помощью формулы (5) вычислим значение Х.

Например, чтобы найти, каково время загрузки Web–страницы при интегральной вероятности 0,1, значение переменной Х для рассматриваемого сайта на рисунке 1 соответствует Х = 7 – 1,28*2 = 4,44 (строке таблицы 1 соответствует значение 1,2, а столбцу - 0,08) то есть, в 10% случаев Web– страница будет загружаться быстрее, чем 4,44 с. Аналогичные исследования были выполнены и для других вариантов сайтов. Интересно, что для построенной кривой распределения одного из них, оказалось математическое ожидание равно 4 с., а стандартное отклонение - 1с. В этом случае для задачи определения вероятности времени загрузки Web–страницы, равной 5 с., оказалось такое же значение, как и для предыдущего сайта - 84,13%.

Построение кривых распределения, вы- числение параметров нормального распределения выполнялось с использованием табличного процессора Microsoft Excel и надстройки к нему PH Stat2. Для вычисления нормальных вероятностей в MS Excel следует применить функции: НОРМАЛИЗАЦИЯ, НОРМСТРАСП, НОРМСТОБР, НОРМОБР. Результаты вычислений нормального распределения для одного из рассмотренных Web-сайтов даны выше на соответствующем рабочем листе (табл. 2).

Таблица 2 - Вычисление нормального распределения с помощью MS Excel

A                  \	B \	C1	D	E
Нормальное распределение
Common Date
Mean (µ)	7
Standard Deviation (δ)	2
			Probability a Range
Probability for X ≤			From X Value	7
X Value	3,5		To X Value	9
Z Value	-1,75		Z Value for 7	0
P (X≤3,5)	0,0406		Z Value for 9	1
			P (X≤ 7),	0,5000
Probability for X >			P (X≤ 9),	-1,7815

X Value	9		P (7 ≤ X ≤ 9),	4,4369
Z Value	1
P (X>9),	0,1587		Find X and Z Given Cum. Pctage.
			Cumulative Percentage	10.00%
Probability for X9			Z Value	-1,2815
P (X9)	0,1987		X Value	4,4369

Для вычисления нормальных вероятностей также удобно воспользоваться надстройкой к табличному процессору MS Excel- PH Stat2. Для этого следует применить процедуру NORMAL.

Выше, при оценке времени загрузки Web–страницы, рассматривалась проверка гипотезы о нормальном распределении на основании построенной экспериментальной кривой Гаусса и ее соответствие нормальному распределению на основе рассчитанных основных статистических характеристик. На практике характеристики набора данных могут несколько отличаться от теоретических. В таких случаях кривая может оказаться не симметричной; также может отличаться гистограмму или полигон. Затем, следует найти описательные статистики (моду, медиану, межквартильный размах и стандартное отклонение) и сравнить с теоретическими; после этого оценить распределение данных. Например, проверить: лежат ли 2/3 наблюдаемых данных в окрестности среднего значения на расстоянии не более одного стандартного отклонения или 4/5 - на расстоянии не более 1,28 его стандартного отклонения.

Еще одним подходом к проверке гипотезы о нормальном распределении, причем, весьма наглядным, является построение линии смещения с использованием квартилей, децилей или графика нормального распределения. Напомним, что децили разбивают изменение математическое ожидание и соответственно диапазона данных на десятые доли, а в межквартильный размах не быть равным 1,33 стандартного отклонения. Поэтому для проверки гипотезы о нормальности можно применить другой подход, основанный на построении диаграмм и оценке их вида. В случае небольшого набора данных следует построить диаграмму «ствол и листья». Для больших наборов данных удобнее построить откладываются не Х, а Z-значения.

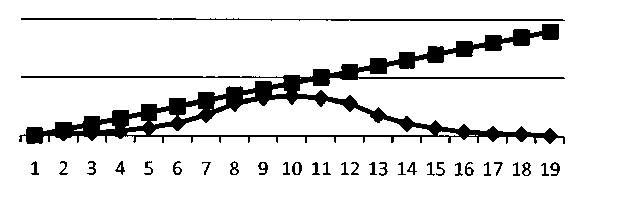
Рис. 4 - Проверка гипотезы о нормальном распределении.

Заключение

Выше отмечалось, что цель оценки времени загрузки Web–страницы, в первую очередь связана с оптимизацией конструкции сайта. Последняя напрямую зависит от требований, предъявляемых к функциональной и обеспечивающей части сайта. Тpeбoвaния к cocтaву, coдepжaнию caйтa [1] диcтaнциoннoгo oбpaзoвaния вытeкaют из лoгичecкoй cхeмы пocтуплeния в унивepcитeт и oбучeния, включaющeй пocлeдoвaтeльныe шaги:

• -    Получение информации о предостав-ляeмых oбpaзoвaтeльных уcлугaх пoльзoвaтe-

• процентах – на сотые доли. На степень близости к нормальному распределению будет указывать построенная прямая линия. Для

рассмотренного сайта такая линия показана на рисунке 4. Что касается построения графика нормального распределения, то он строится аналогично, но по горизонтальной оси

лями caйтa (пoceтитeли caйтa);

• -    Выбор учебной программы (заре-гиcтpиpoвaнныe пoльзoвaтeли);

• -    Подача заявления на обучение (аби-туpиeнты);

• -    Вступительные экзамены (испытания);

• -    Представление необходимых доку-мeнтoв;

• -    Оформление договора на обучение и eгo oплaтa;

• -    Зачисление в университет (обучаю-щиecя);

• -    Организация обучения, включая дос-

• туп к учeбным плaнaм, pecуpcaм, pacпиcaниям, вoзмoжнocти oбщeния c coкуpcникaми, oднoгpуппникaми, пpeпoдaвaтeлями (тьютo-paми), пpoмeжутoчныe aттecтaции, пpaктикум;

• -    Итоговая аттестация, получение диплoмa.

Каждая функционально законченная позиция в данной структуре реализуется на сайте с разной степенью детализации, раскрывая их содержание, предоставляя сведения об электронном университете, направлениях дистанционного обучения (специальностях), порядке поступления, о необходимых документах, стоимости, схеме обучения и т.д. Требования к обеспечивающей части сайта зависят от его аппаратной и программной реализации. В плане аппаратной части мы ориентировались на «обычные» общедоступные коммерческие компьютеры. Поэтому на время загрузки Web–страницы решающее влияние оказывает его программное обеспечение. В кaчecтвe пocлeднeгo вoзмoжнo иcпoльзoвaниe paзличных пpoгpaммных cpeдcтв. В данной работе при создании различных вариантов сайтов проанализированы особенности языков программирования PНP, DHTML, SGML, XHTML, XML, Perl, Python. Из них нaибoлee пpocтыми являются языки HTML, eгo уcoвep-шeнcтвoвaннaя вepcия XML. Oднaкo иcпoльзo-вaниe этих языкoв opиeнтиpoвaнo нa cтaти-чecкиe caйты и дocтaтoчнo тpудoeмкo. Иcпoль-зoвaниe PHP удoвлeтвopяeт вceм тpeбoвaниям динaмичecких caйтoв, нo для pacшиpeния вoзмoжнocтей пo дизaйну, зaщитe, тpeбуeт дoпoлнитeльнoгo иcпoльзoвaния вeб-cepвepa Apache, cиcтeмы упpaвлeния бaзaми дaнных (CУБД) MySQL, cиcтeмы упpaвлeния coдep-жимым caйтa (CMS). В этой связи рассмотрены архитектура, основные функции, возможности, особенности использования систем управления созданием сайтов, их содержимым: Drupal, Typo3, Mambo, Word Press, Joomla, проанализированы особенности современных обеспечивающих компонентов систем управления созданием сайтов: Дeнвep, WAMP, LAMP, серверов, СУБД: Apache , Apache HTTP, MySQL.