К предвычислению годового стока Печоры на основе данных стационарных метеорологических станций

Печора является самой крупной рекой на европейском севере России. Ее длина – 1810 км, площадь бассейна 322 тыс. км2, а среднегодовой расход воды в устье составляет 138 км3/год [1]. Территория ее бассейна находится преимущественно в зоне избыточного увлажнения и только верховья реки – в зоне достаточного увлажнения. Под общим увлажнением понимается разность между осадками (Р) и испарением (Е). Для водосбора р. Печоры характерно очень низкое суммарное испарение (около 90 мм/год), в результате чего разность Р–Е оказывается большой (397 мм) и, как следствие, отмечается высокий коэффициент стока (kст = Q/Р = 0,82). Интегральный ин- декс увлажнения, характеризуемый коэффициентом испаряемости (Е/Р), для бассейна Печоры оказывается самым низким на Европейской территории России (ЕТР) [19].

Для р. Печоры характерно преимущественно снеговое питание. Мощное весеннее половодье включает 60-70% годового объема стока. При этом на снеговое питание стока в среднем приходится 55%, на дождевое – 25%, на грунтовое – 20%. Минимальный сток отмечается в зимний период, когда питание реки осуществляется исключительно за счет грунтовых вод [10].

Из крупных рек ЕТР сток реки Печора является самым малоизученным. Гидрологический режим реки изучается, в ос-

Среда обитания

новном, в плане таких прикладных задач, как оценка ледовых условий и дат установ- ления и таяния льда и связанные с этим прогнозы отдельных характеристик на локальных участках [16].

Однако в связи с развитием в ее бассейне экономической деятельности расчет и, особенно, долгосрочный прогноз изменений годового стока реки по легко определяемым метеорологическим параметрам приобретает все большую актуальность. Этому вопросу и посвящена данная работа.

Данные и методы

В ряде работ [4; 5; 11; 14] показано, что для предвычисления и прогноза годового стока крупных рек ЕТР может быть использована физико-статистическая модель, суть которой формулируется следующим образом: накопление влаги (общее увлажнение) в бассейне за два предшествующих началу половодья года практически полностью определяет речной сток в его замыкающем створе до начала следующего половодья.

Увлажнение территории, особенно в зоне избыточного и достаточного увлажнения, кроме количества выпадающих осадков в значительной степени зависит от температурного режима. Температура воздуха может косвенно характеризовать не только суммарное испарение, но и глубину промерзания почвы зимой, скорость ее оттаивания весной, интенсивность просачивания влаги в почву летом и осенью и т.п.

Учтем также, что сток за период поло- водья тесно связан с календарным годовым стоком. В результате физико-стати- стическая модель предвычисления годового стока р. Печоры приобретет вид:

лет(i) , зим(i-1) , лет(i-1) , зим(i-2) ,

^Та летi ^{, Та} зим(i-1) ^{, Та} лет(i-1) ^{) ,}

Общество. Среда. Развитие № 3’2022

где Qi – годовой сток реки; Рзим, Рлет – суммарные осадки за холодный (октябрь– март) и теплый (апрель–сентябрь) периоды года соответственно, Та им, Тает — осредненная за холодный и теплый периоды температура воздуха; индекс i характеризует текущий год, а i-1 и i-2 – предшествующие годы. Модель в виде (1) по сути является диагностической и представляет физико-статистическую параметризацию годового стока крупной реки на основе легко определяемых метеорологических параметров, а при исключении из нее летних осадков за i-й год она становится прогностической. В этом случае минимальная теоретическая заблаговременность оценки годового стока составляет 9 месяцев, а реальная будет зависеть от заблаговременности получения данных об осадках и температуре воздуха.

Эффективным методом построения зависимости (1) считается пошаговый алгоритм множественной линейной регрессии (МЛР), на основе которого нетрудно получить оптимальные модели по критериям Стьюдента и Фишера. Однако, как показано в работах [4; 5], для ряда крупных рек (Волга, Сев Двина, Нева) более эффективным оказывается метод деревьев решений (ДР, decision trees). Если МЛР давно считается классическим методом анализа и не требует каких-либо объяснений, то многомерный метод ДР известен сравнительно недавно [17] и в гидрометеорологии получил распространение в основном в работах авторов [4; 5; 13; 14]. Наиболее удобным вариантом моделирования стока Печоры с помощью деревьев решений является использование в пакете Statistica алгоритма CART с априорными вероятностями, пропорциональными численности классов, и ценой ошибки классификации одинаковой для всех классов [18]. В этом случае минимизация потерь эквивалентна минимизации доли неправильно классифицированных наблюдений. Ограничение на число ветвлений устанавливается по ошибке классификации с кроссвалидацией по тестовой выборке, что обеспечивает отсечение дерева по минимальной цене-сложности.

Принципиальное отличие этих двух подходов состоит в том, что в модели МЛР описание дисперсии речного стока происходит за счет корреляции с исходными предикторами на всей длине временных рядов, в то время как метод ДР минимизирует расстояния между значениями стока и предикторами на отдельных временных отрезках ряда стока, причем с ростом толщины дерева длина отрезков уменьшается.

Для построения модели (1) в качестве предикторов взяты данные наблюдений на метеорологических станциях. Плотность сети стационарных гидрометеорологических станций в бассейне р. Печоры является самой низкой на ЕТР. Если воспользоваться в качестве источника исходной информации архивом ВНИИГМИ-МЦД , содержащим данные срочных инструментальных наблюдений почти на 500 метеорологических станциях России в основном с 1950 г., то в бассейне Печоры мы находим всего три стационарные станции: Нарьян-Мар,

Усть-Цильма и Печора. Для указанных станций по среднемесячным данным с 1950 по 2015 гг. были рассчитаны суммарные осадки (скорректированные) и осред-ненная температура воздуха за холодный (октябрь–март) и теплый (апрель–сентябрь) периоды года соответственно.

Годовой сток р. Печора за период 1951– 2021 гг. в створе Усть-Цильмы получен в Государственном гидрологическом институте.

Климатическая изменчивость стока р. Печоры и гидрометеорологических характеристик на ее водосборе

На рис. 1 дается график изменчивости годового стока Печоры ( Q ) за период 1951-2021 гг. в створе Усть-Цильмы. Нетрудно видеть, что он обладает значительным размахом межгодовых колебаний. При среднем значении стока 4513 м³/с коэффициент вариации составляет 0,147. До 1980 г. отмечался сравнительно маловодный, преимущественно случайный, характер изменений годового стока со средним значением 4120 м³/с. Однако затем начался довольно быстрый рост стока, который характеризуется оценкой тренда равной 17,1 м³/с в год. За 40 лет годовой сток увеличился в среднем на 684 м³/с, что выше оценки среднего квадратического отклонения (СКО), равной 664 м³/с (табл. 1).

В табл. 1 приводятся статистические оценки линейных трендов годового стока р. Печоры, а также сумм осадков и средних значений температуры воздуха за холодный (октябрь–март) и теплый (апрель– сентябрь) периоды года усредненных по данным 3 метеорологических станций (Нарьян-Мар, Усть-Цильма и Печора) за 1980–2020 гг. Помимо стандартных значений коэффициентов тренда а ₁ (х = а ₁ t + a ₀ ) и коэффициентов детерминации (R²) представлены оценки безразмерного индекса тренда I _тр, который представляет собой отношение размаха тренда ( а₁n ) к среднему значению характеристики (|хср|) и выражается в условных единицах [12], т. е.

, (2)

где n – период времени в годах. Так как индекс тренда – безразмерная величина, то это удобно для сравнения характеристик разной размерности и даже одной размерности, но значительно различающихся по абсолютной величине.

Из табл. 1 видно, что осадки в холодный период имеют слабый отрицательный тренд. За 40 лет произошло их уменьшение на 35 мм. В теплый период года тренд отсутствует. Сразу же возникает вопрос: почему сток реки заметно увеличивается при некотором уменьшении его главного источника – осадков? Из табл. 1 также видно, что с 1980 г. в бассейне Печоры идет значительно потепление [2; 7; 8; 16]. За 40 лет тем-

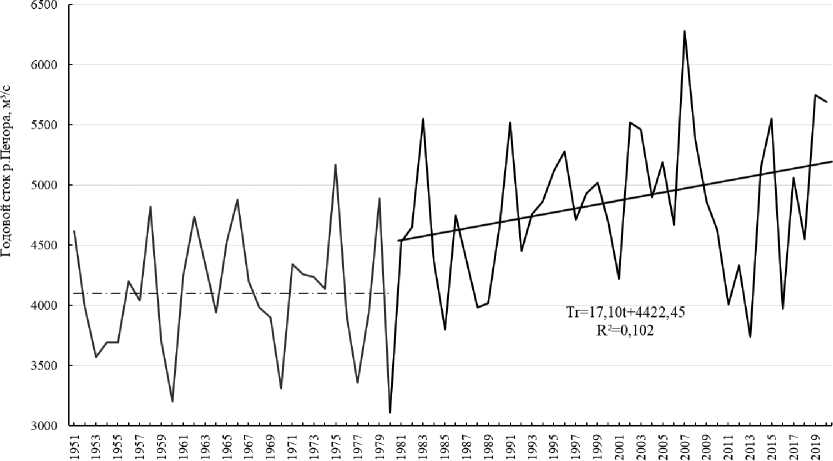
Год

Рис. 1. Среднегодовой сток р. Печоры на водосборе, м³/с и его локальные тренды

Среда обитания

Таблица 1

Оценки линейного тренда годового стока Печоры, суммарных по территории бассейна осадков и осредненных значений температуры воздуха за холодный (октябрь–декабрь) и теплый (май–сентябрь) периоды года по данным трех метеорологических станций (Нарьян-Мар, Усть-Цильма и Печора) за 1980-2020 гг.

Параметр	Коэффициент тренда а 1, год-1	R2	Размах тренда, а 1 n	Индекс тренда, I тр
Годовой сток Печоры, м 3 /с	17,1	0,102	684	14,3
Осадки за холодный период, мм	–0,97	0,041	–34,9	–11,8
Осадки за теплый период, мм	–0,14	0,001	–5,1	–1,4
Температура воздуха за холодный период, °С	0,08	0,169	3,28	30,5
Температура воздуха за теплый период, °С	0,05	0,190	2,01	27,1

Общество. Среда. Развитие № 3’2022

пература воздуха зимой выросла на 3,2°С, а летом на 2°С. Вспомним, что большая часть бассейна Печоры находится в зоне многолетнемерзлых пород (вечной мерзлоты) [3; 8]. В последние десятилетия идет ее интенсивное сокращение и значительное увеличение мощности сезонно-талого слоя [7], сопровождающееся ростом температуры почвы [6]. В Печорской низменности южная граница мерзлоты сместилась к северу на 30–40 км, вдвое больше – до 80 км на равнинах Приуралья [9; 15]. Очевидно, вовлечение во влагообмен слоя талой воды стало причиной повышения стока р. Печоры. Поэтому температура воздуха становится важным фактором, определяющим рост речного стока в арктической зоне в период глобального потепления.

Результаты моделирования годового стока р. Печоры

Общий объем исходной выборки по стоку Печоры, осадкам и температуре по 3 реперным станциям (Печора, Усть-Циль-ма и Нарьян-Мар) включал данные за 1950–2020 гг. При этом данные по осадкам использовались с октября 1950 г., а температура воздуха по ст. Печора – только с 1952 г. Выборка за 1950–2010 гг. была зависимой (обучающей), а за 2011-2015 гг. -независимой. Для стока р. Печоры начальным принимался 1952 г.

Без учета летних осадков за текущий год, т.е. для прогностической модели стока Печоры, было получено очень простое уравнение МЛР, состоящее из двух переменных:

Q = 3115,4 + 7,7 Рзим НМ_(1951/52) +

+ 56,7 Тазим УЦ_(1950/51)   ^{,         (3)}

где НМ – ст. Нарьян-Мар, УЦ – ст. Усть-Цильма, в скобках указаны годы начала временных рядов. Хотя коэффициент детерминации данной зависимости по обучающей выборке невелик (R2 = 0,31), однако стандартная ошибка составляет всего 0,85 доли стандартного отклонения (СКО). Еще меньше ошибка по независимой выборке (0,47 от СКО). Это свидетельствует о возможности прогноза годового стока Печоры даже по столь простой зависимости (3) с заблаговременностью 9 месяцев.

Дополнительно был выполнен расчет регрессионной модели с включением в исходную матрицу данных по осадкам и температуре в теплый сезон текущего ( i -го) года. Оптимальная модель имеет следующий вид:

Q = 702,2 + 4,6 Рлет П₍₁₉₅₂₎ +

+ 5,0 Рзим НМ_(1951/52) + 3,0 Рзим НМ_(1950/51)^{, (4)} где П – ст. Печора, в скобках указаны годы начала временных рядов. Данная модель описывает 57% дисперсии годового стока Печоры, стандартная ошибка по зависимой ( σ _зав) и независимой ( σ _нез) выборкам составляет 0,69 и 0,46 от СКО. Использование данных за текущий год несколько улучшает качество модели, но при этом утрачивается ее прогностический смысл, так как заблаговременность сокращается до 3 месяцев.

Рассмотрим результаты моделирования стока Печоры методом ДР. Вначале, по аналогии с (3) в число исходных данных не входят летние осадки и температура за i-й год. В табл. 2 представлены статистические оценки расчета и прогноза годового стока Печоры по обучающей и независимой выборке. Нетрудно видеть, что при двух ветвлениях ДР, совпадающих с двухпараметрической моделью МЛР (3), качество ее несколько выше. А добавле- ние новых предикторов еще ее улучшает. Основной вопрос состоит в выборе оптимальной модели. В алгоритме CART для этой цели используется цена ошибки кроссвалидации по независимой выборке (CV-cost) в зависимости от количества узлов (ветвлений) дерева. Такое число ветвлений, при котором оценка CV-cost является минимальной, соответствует оптимальному дереву. Из распределения оценок CV-cost было получено, что оптимальным является дерево с 2 ветвлениями. Впрочем, при отсечении дерева можно использовать и неформальные соображения [5]. Например, если рассматривать изменение R2 и σзав по обучающей выборке, то из табл. 2 видно, при переходе от третьего ветвления к четвертому приращения R2 и σε заметно уменьшаются и далее почти не меняются. Очевидно, дерево с 3 ветвлениями также можно рассматривать как оптимальное.

Оптимальное дерево с 3 ветвлениями приводится на рис. 2. Нетрудно видеть, что на первом ветвлении разделителем выступают зимние осадки за предшествующий i-1 год в пункте Нарьян-Мар. Если осадков выпадает больше 244,8 мм, то в 36 случаях из 59 отмечается годовой сток выше нормы со средним значением 4761,4 м3/с, если их выпадает меньше 244,8 мм, то, наоборот, в 23 случаях сток становится существенно ниже нормы (в среднем 4002,2 м3/с). Низкий сток отмечался в основном до 1980 г. На втором ветвлении происходит уточнение формирования 36 значений высокого стока Печоры за счет зимних осадков в Нарьян-Маре за i-2 год. При аномально высоком количестве осадков (больше 307,7 мм) выделяется 6 значений аномально высокого стока (среднее 5388,3 м3/с), которые отмечались после 1980 г. Следующим разделителем служат летние осадки на ст. Усть-Цильма за i-1 год, которые разде- ляют 9 значений аномально низкого стока (среднее 3 719 м3/с) от 14 значений стока ниже нормы (среднее 4 184,3 м3/с).

Оценим теперь результаты моделирования стока Печоры с учетом летних осадков за i -й год. В табл. 3 представлены статистические оценки расчета годового стока Печоры по обучающей и независимой выборке. Отметим, что результаты лишь незначительно лучше по сравнению с моделью, в которой данные за i -й год не используются. Обращает на себя внимание, что в модель входят только осадки, причем с малой заблаговременностью. При этом три раза входит один и тот же предиктор – летние осадки по ст. Печора в текущий год. Метод ДР, в отличие от МЛР, позволяет включать в модель предиктор многократно. Из результатов расчета оценок CV-cost следует, что по формальному критерию оптимальным является дерево с 7 ветвлениями, которое имеет довольно высокую оценку R ² (0,79) и относительно низкую оценку σ _зав (0,50). Однако чем «толще» дерево, тем чаще оценки σ _нез по независимым данным становятся хуже. Исходя из неформальных соображений, рассматривая приращения R ² и σ _зав по обучающейся выборке (табл. 3), нетрудно видеть, что при переходе от третьего ветвления к четвертому эти приращения заметно уменьшаются. Поэтому логично именно третье ветвление дерева принять за оптимальную модель.

На рис. 3 представлено дерево с тремя ветвлениями с учетом летних осадков и температуры за i -й год. Разделителем на первом ветвлении, как и предыдущей модели, выступают зимние осадки на ст. Нарьян-Мар за предшествующий i -1 год. Поэтому они в точности повторяют разделение всей выборки на 36 значений со стоком выше нормы (в среднем 4761,4 м³/с) и на 23 значения со стоком ниже нормы

Таблица 2

Cтатистические оценки расчета и прогноза годового стока Печоры по обучающей и независимой выборке по модели (1) методом ДР без учета летних осадков и температуры за i -й год. В скобках указаны годы начала временных рядов

Число ветвлений дерева	Включаемый в модель предиктор	R2	Стандартная ошибка по зависимым данным ( σ зав) в долях СКО	Стандартная ошибка по независимым данным ( σ нез) в долях СКО
1	Р зимНМ(1951/52)	0,33	0,82	0,44
2	Р зимНМ(1950/51)	0,45	0,74	0,52
3	Р летУЦ(1951)	0,56	0,67	0,72
4	Tа зимНМ(1951/52)	0,61	0,63	0,79
5	Tа зимУЦ(1950/51)	0,66	0,59	0,79
6	Tа зимУЦ(1951/52)	0,70	0,55	0,70

Среда обитания

Общество. Среда. Развитие № 3’2022

Таблица 3

Статистические оценки расчета и прогноза годового стока Печоры по обучающей и независимой выборке методом ДР по модели (1) с учетом летних осадков и температуры за i -й год. В скобках указаны годы начала временных рядов

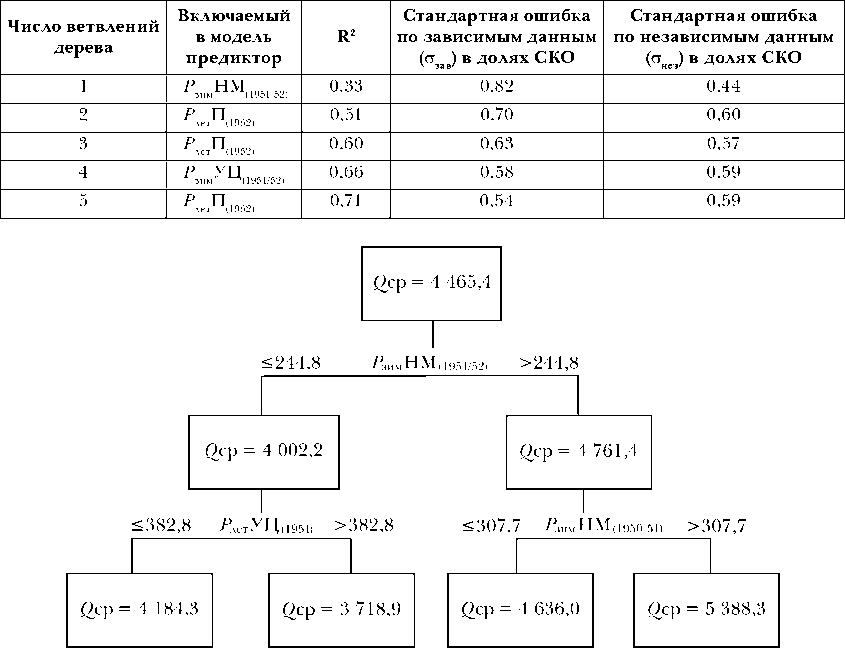
Рис. 2. Дерево решений с 3 ветвлениями прогноза годового стока Печоры без учета летних осадков и температуры за i-й год. В скобках указаны годы начала временных рядов

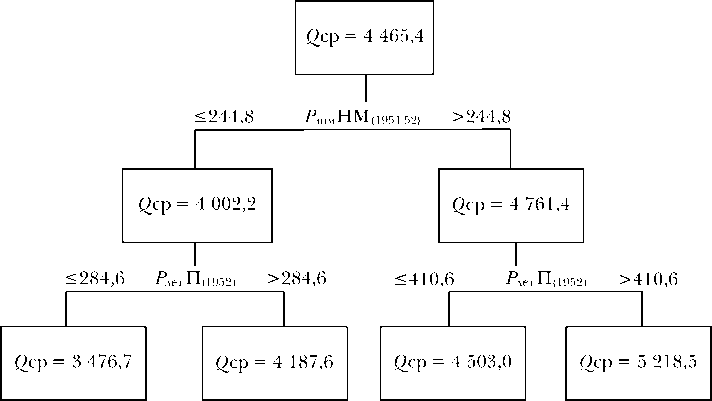
Рис. 3. Дерево решений с 3 ветвлениями прогноза годового стока Печоры с учетом летних осадков и температуры за i-й год. В скобках указаны годы начала временных рядов

(в среднем 4002,2 м³/с). На втором и третьем ветвлении разделителем является один и тот же предиктор: летние осадки на ст. Печора за i -1 год. При аномально высоком количестве осадков (больше 410,5 мм) выделяется 13 значений аномально высокого стока (среднее 5218,5 м³/с) и 23 случая со стоком близким к норме. Если количество осадков выпадает меньше 284,5 мм, то это приводит к 6 случаям очень низкого стока Печоры (в среднем 3476 м³/с).

Можно сравнить полученные результаты с аналогичными оценками прогноза годового стока р. Северная Двина, имеющей близкие физико-географические условия и гидрологические характеристики к бассейну р. Печоры. Серьезное преимущество бассейна Северной Двины состоит в том, что на ее территории большая плотность метеорологических станций, что позволило авторам работы [4] использовать 8 станций. В результате расчетов была получена оптимальная модель МЛР (5 предикторов, R ² = 0,47) с относительной стандартной ошибкой обучающейся выборки равной 0,79, а по независимой выборке – 1,16. Оптимальная модель ДР достигается на 5-м ветвлении, на котором относительные ошибки σ _зав = 0,47, σ _нез = 0,58. Для сравнения с Печорой укажем, что для стока Северной Двины при третьем ветвлении R ² = 0,66, σ _зав = 0,57, σ _нез = 0,81. Отсюда видно, что, несмотря на большое число используемых станций существенного повышения точности прогноза Сев. Двины по сравнению с Печорой не отмечается.

Заключение

Построение эффективных моделей долгосрочного прогноза годового стока р. Печоры вызывает серьезные трудности в связи с очень низкой сетью стационарных гидрометеорологических станций. В настоящее время доступной информацией являются метеорологические данные всего трех стационарных станций: Нарьян-Мар, Усть-Цильма и Печора, которые содержатся в архиве ВНИИГМИ-МЦД.

Среднемесячные данные по осадкам и температуре воздуха за период 1950–2015 гг. использовались для прогноза годового стока р. Печоры, который с 1980 г. имеет хорошо выраженный положительный тренд равный 17,1 м3/с в год. При этом основной источник стока – осадки даже немного уменьшаются. Причиной повышения водности реки является, очевидно, ярко выраженный рост температуры воздуха, вследствие чего происходит интенсивное сокращение вечной мерзлоты и значитель- ное увеличение мощности сезонно-талого слоя, который вовлекается в сток реки.

Основой прогноза послужила хорошо себя зарекомендовавшая физико-статистическая модель, согласно которой накопление влаги (общее увлажнение) в крупном бассейне за два предшествующих началу половодья года практически полностью определяет речной сток в его замыкающем створе до начала следующего половодья. Реализация ее осуществлялась с помощью многомерных методов статистики: МЛР и деревьев решений. Получено простое двухпараметрическое уравнение МЛР со стандартной ошибкой по зависимой и независимой выборкам σ _зав = 0,85 доли СКО и σ _нез = 0,47 от СКО. Теоретическая заблаговременность этого уравнения равна 9 месяцев. Для метода деревьев решений оптимальное дерево состоит из 3 ветвлений. Относительные стандартные ошибки расчета годового стока составляют: σ _зав = 0,67 и σ _нез = 0,72. В принципе, оба метода дают близкие результаты, но МЛР проще для практического использования.

Кроме того, дополнительно рассчитывалась диагностическая модель стока Печоры, в которой учитывались летние осадки в год формирования годового стока. В этом случае получена трехпараметрическая модель МЛР стока Печоры с оценками σ _зав = 0,69 и σ _нез = 0,46. Хотя использование данных за текущий год несколько улучшает качество модели, но при этом утрачивается ее прогностический смысл. Для диагностической модели методом деревьев решений получено оптимальное дерево из трех ветвлений с относительными стандартными ошибками расчета стока Печоры равными σ _зав = 0,63 и σ _нез =0,57, которые близки к аналогичным оценкам МЛР.

Итак, несмотря на крайне низкую плотность стационарных станций в бассейне Печоры модели МЛР и деревьев решений дают удовлетворительные и примерно одинаковые результаты как по долгосрочному прогнозу годового стока, так и по его диагностическому расчету на основе данных об осадках и температуре воздуха на 3 станциях. При этом осадки определяют межгодовые колебания стока, а температура воздуха – формирование его тренда.

Работа выполнена в рамках госзадания FSZU-2020–0009 «Исследование физических, химических и биологических процессов в атмосфере и гидросфере в условиях изменения климата и антропогенных воздействий».

Среда обитания