К расчету моментных функций решения системы линейных параметрических стохастических интегро-дифференциальных уравнений нейтрального типа
Автор: Полосков И.Е.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 2 (37), 2017 года.
Бесплатный доступ
Рассматривается проблема построения обыкновенных дифференциальных уравнений для первых и старших моментных функций решения системы линейных параметрических стохастических интегро-дифференциальных уравнений нейтрального типа. На основе схемы, сочетающей классический метод шагов и расширение пространства состояния, построена цепочка стохастических дифференциальных уравнений без запаздывания, а затем и уравнения для математического ожидания, дисперсии и моментных функций порядка выше второго. Приводится пример применения схемы.
Стохастический анализ, моделирование, линейная параметрическая система, решение, расширение пространства состояния, моментные функции
Короткий адрес: https://sciup.org/14730104
IDR: 14730104 | УДК: 519.21 | DOI: 10.17072/1993-0550-2017-2-35-48
Текст научной статьи К расчету моментных функций решения системы линейных параметрических стохастических интегро-дифференциальных уравнений нейтрального типа
Теория и применения функциональнодифференциальных уравнений (ФДУ) [1-5, 8], в которых эволюция во времени переменной или переменных состояния может зависеть от прошлого в произвольной форме, стали важной частью современной нелинейной динамики. За последние несколько десятилетий эти уравнения нашли широкое применение в различных областях науки и техники, являясь адекватным и незаменим инструментом математического моделирования реальных процессов в технике, обществе, живой и неживой природе, которые характеризуются наличием последействия в различных формах и наследственности ма-
териалов (механика материалов с памятью, теория (термо)вязкоупругости, гибридные модели). Применения ФДУ в прикладных областях разнообразны и многочисленны, например, в физике, химии, экономике, в теории управления техническими системами, химико-технологическими и другими производственными процессами (например, холодной прокатки стали), навигации, теории информации, общей и популяционной биологии, экологии, в эпидемиологии, физиологической, фармацевтической и химической кинетике, медицине, при генерации сигналов в радиосхемах и лазерах, описании процессов в теплообменниках, горения в жидкостно-реактивных двигателях, замедления нейтронов и др. Математическая теория ФДУ является областью теории диф- ференциальных уравнений, которая быстро развивалась и характеризуется значительными достижениями за последние 50 лет.
В настоящее время существует несколько основных областей исследования ФДУ, где ведутся интенсивные научные разработки. Среди них качественный анализ существования и устойчивости решений ФДУ, изучение чувствительности и явлений синхронизации; прямое количественное исследование линейных систем, в первую очередь, на основе применения классического метода шагов; использование процедур усреднения ДУ с учетом малости запаздывания; построение различных численных интеграторов, а также методик получения частных решений задач [4, б, 7] и т.д.
Но анализ систем, описываемых ФДУ, встречает значительные трудности. Как правило, обычные схемы исследования нелинейных систем (линейный анализ устойчивости, изучение бифуркаций, стандартные методы возмущений) непригодны для анализа ФДУ, решения которых обладают новыми свойствами (например, возможна автосинхронизация с временным запаздыванием; даже в системах первого порядка допустимы колебательные режимы за счет наличия периодических запаздываний). Присутствие последействия может приводить к неустойчивой и неудовлетворительной работе технических устройств, а также их плохой управляемости.
Моделирование физических систем с помощью обыкновенных дифференциальных уравнений (ОДУ) игнорирует стохастические эффекты. Путем добавления случайных процессов (СП) в дифференциальные уравнения получаем математические объекты, называемые стохастическими обыкновенным дифференциальными уравнениями (СДУ, СОДУ), а указанные СП - шумами или флуктуациями. Такие модели обеспечивают более точное описание явлений. Начальные условия, как правило, также являются также случайными. В результате этого решение одного или системы СОДУ - скалярный или векторный СП. При этом СО
ДУ играют важнейшую роль при моделировании процессов во многих прикладных областях.
В значительном числе отраслей науки и техники СОДУ с запаздыванием (СО-ДУсЗ), являющиеся естественными обобщениями СОДУ, используются для описания явлений, где как и в детерминированном случае, существенное влияние на поведение объектов оказывают задержки в различных формах [1, 4, 9-11]. При этом для построения стохастических моделей случайные возмущения нередко просто вводятся в соответствующие детерминированные дифференциальные уравнения, получая таким образом СОДУсЗ. Вопросы, связанные с определением СИДЕ, существованием и единственностью их решений рассмотрены в [12,13].
Различают СОДУ (дифференциальноразностные и нейтральные) с конечными одиночными или множественными дискретными запаздываниями (постоянными или переменными, детерминированными или случайными) и ограниченными или неограниченными распределенными запаздываниями. Такие формы СОДУсЗ описываются стохастическими обыкновенными интегро-дифференциальными уравнениями Воль-терры (СОЙДУ). Дальнейшее усложнение моделей приводит к использованию смешанных форм СОДУсЗ, включающих как дискретные, так и распределенные запаздывания1 . Но исследование таких систем вызывает значительные трудности.
Стохастические функционально-дифференциальные системы служат моделями во многих областях науки. Например, СОЙДУ, которые охватывают значительную область динамики систем, используются для описания обратной связи, транспортных потоков, работы лазеров, реакторов, теплообмена за счет теплопроводности и излучения, резки металла, гистерезиса, вязкоупругости, генного регулирования, передачи нервных импульсов и инфекционных заболеваний и т.д.
В течение последних нескольких десятилетий проводились многочисленные иссле-
ХВ данной работе мы ограничивается моделями в форме СОДУсЗ, по в рамках области стохастических ФДУ активно исследуются СДУсЗ в частных производпых(СДУвЧПсЗ), а также гибридные формы СОДУсЗ и СДУвЧПсЗ.
дования СОДУсЗ и СОИДУсЗ, которые были посвящены изучению вопросов существования и единственности решений, асимптотического их поведения, решению задач анализа бифуркаций, синхронизации, самоорганизации, устойчивости, управления, стохастического резонанса, идентификации, фильтрации и др. Кроме этих проблем, естественно интенсивно развиваются аналитические, численные и приближенно аналитические методы построения сильных (реализаций) и слабых (моментных характеристик) решений таких уравнений.
Среди стохастических ФДУ можно выделить класс линейных и нелинейных СОДУ с конечными сосредоточенными и распределенными запаздываниями. Детерминированные аналоги таких уравнений могут принимать форму как обыкновенных дифференциальных, так и дифференциальных уравнений в частных производных [14], а использоваться при моделировании роста населения, загрязнения окружающей среды, поведения финансовых рынков, различных процессов в электрических цепях и химических реакторах, для регулирования соотношения глюкоза-инсулин при диабете, анализа поведения нейронных сетей, человеческих чувств [15,16] и др.
Кроме того, к системам стохастических ОИДУ часто приходят в результате применения процедур типа метода конечных элементов или метода конечных разностей к стохастическим ИДУ в частных производных, которые описывают непрерывную вязкоупругую среду. Основными задачами анализа подобных детерминированных систем являются поиск критериев существования решения и оценка устойчивости как самих решений этих уравнений, так и схем их численного интегрирования. Отметим, что основными приближенными методами в этой области являются конечно-разностные процедуры, различные варианты методов Рунге-Кутты, трапеций, коллокаций [14,17] и др. Алгоритмы же численного или приближенно аналитического интегрирования стохастических систем рассматриваемой структуры развиты недостаточно. При этом было бы полезно адаптировать существующие методы анализа детерминированных ОИДУ для изучения стохастических, так как основная часть алгоритмов качественного и количественного исследования явлений, описываемых СОЙДУ, состоит из детерминированных схем.
Дело в том, что, как правило, прямое исследование систем СОЙДУ невозможно, а аналитическая теория, аналогичная созданной для марковских случайных процессов [18], отсутствует. С другой стороны, имеются работы, где с помощью увеличения размерности вектора состояния интегро-дифференциальные системы, у которых элементы вырожденных матричных ядер представляют собой простейшие функции типа ce—v(:-T ) (c, v - постоянные), приводят к формам, описываемым СДУ, что позволяет для их исследования применить известные точные и приближенные методы [18]. Более того, кроме точных, существует и ряд приближенных схем для упрощения интегральных ядер, таких как использование рядов Прони и аппроксимации полиномами Лагерра для представления функций релаксации [19], метод приближения переходных функций экспонентами [20], приближенный вывод уравнения Фоккера-Планка-Колмогорова для СОЙДУ [21], расширение пространства состояния в случае ограниченности носителя ядра [22] и т.д. Основная цель таких упрощений та же, что и вышеупомянутая.
Среди приближенных методов следует отметить технику перехода от немарковских систем с малыми запаздыванием т (в том числе переменным и случайным) или памятью с помощью метода усреднения к марковским системам без запаздывания. Конечно, нельзя забывать и о прямом численном интегрировании стохастических ФДУ [11]. При этом даже алгоритм основного метода - простейшей схемы Эйлера-Маруямы с постоянным шагом, приводящий к значительным объемам расчетов, существенно сложнее своего аналога, предназначенного для анализа стохастических дифференциальных уравнений без запаздывания [23].
Несмотря на трудности, был разработан ряд других процедур для получения численных аппроксимаций решений детерминированных и стохастических ОИДУ. При анали- зе стохастических задач приближенные алгоритмы, как правило, используются для прямого построения реализаций случайных процессов как решений СОЙДУ. Среди таких схем отметим:
- полностью численные методы (классические и модифицированные гибридные), такие как явные и неявные (обратные) схемы Эйлера, метод конечных разностей, метод конечных элементов, метод полудискретизации, тау-метод, одношаговые методы Рунге-Кутты и многошаговые схемы для ОИДУ, метод Рунге-Кутты для вычисления ковариационных функций, экстраполяционные схемы, методы Галёркина, метод итераций на последнем шаге, использование вейвлетов, глобально определенных базисных Smc-функций, приближенное преобразование СОЙДУ в СОДУ на основе усреднения ядра и разложений гамма-распределения, метод прямоугольников и более сложные схемы интегрирования [20,24-43];
- приближенно аналитические методы, включающие методы рядов Тейлора, метод последовательных приближений для вычисления функции Грина, асимптотические методы для ОИДУ, детерминированный и стохастический методы усреднения для СОЙДУ, метод многих масштабов, метод коллокаций, теория возмущений, принцип неподвижной точки на основе биортогональных систем для банаховых пространств, итерационный метод, непрерывные методы Рунге-Кутты, основанные на методе коллокаций, преобразование Лапласа для одномерной ограниченной пространственной области, методы Эйлера-Чебышёва [44-59] и др.
В ряде наших предыдущих работ была предложена схема, сочетающая классический метод шагов и расширение пространства состояния (МШРПС), в приложении к исследованию стохастических систем с различными формами запаздыванием, включая некоторые виды СОЙДУ [22,40,60-72]. Ниже рассматривается методика исследования линейных параметрических нейтральных стохастических систем с конечными сосредоточенными и распределенными запаздываниями, основанная на модификации указанной схемы.
1. Постановка задачи
Рассмотрим систему линейных параметрических стохастических обыкновенных интегро-дифференциальных уравнений Стратоновича нейтрального типа в следующей форме:
X (t) = A (t) X (t) + c (t)+
+ R(t) X (t — т ) + Q(t) X (t — т ) +
t
+ B (t) jx (0) de + [H (t): X (t) + t-τ
+ Q(t) : X(t — т) + H(t)] V(t), t > ti = to + т, (1.1)
где t - время, т > 0 - сосредоточенное запаздывание. X(t) = {Xi(t)} G Rn - векторный случайный процесс (ВСП), представляющий собой решение системы уравнений (1.1): V(t) = {Vj(t)} G Rm - векторный случайный процесс, компонентами которого являются независимые стационарные гауссовские процессы типа стандартных белых шумов: E[V(t)] = 0. E [V (t1 ) Vт(t2)] = I$(t2 — ti); E [ • ], т ^ символы математического ожидания и транспонирования матриц; I - единичная матрица.
Будем считать, что на интервале (to,ti] СП X(t) удовлетворяет системе линейных параметрических стохастических обыкновенных дифференциальных уравнений без запаздывания
X(t) = A o(t) X(t) + c o(t)+
+ [ Ho(t): X (t) + Ho(t)] V (t), (1.2) с начальным условием
X (to)= X 0, (1.3)
причем в уравнениях (1.1) и (1.2) A(t) = { aij(t) }. B(t) = { bi,-(t) }. H(t) = {hij (t) }. R(t) = { rij(t)}. Q(t) = { qij(t)}. A o(t) = { aoij(t) }. Ho(t) = { hoi,-(t)}: !H(t) = { hijk(t) }. Q(t) = { qijk(t) }. Ao (t) = { hoijk(t) } 11 c (t) = { ci(t) }. c o(t) = { coi(t) } - известные непрерывные матричные, трехмерные матричные и векторные функции переменной t;
И o(t) : X (t) ^ {]Т hoijk (t) Xk (t)} k=1
(i = 1,n. j = 1,m). Кролю того, предположим, что известны все необходимые числовые характеристики векторной случайной величины (ВСВ) X0 = {Xi0} G Rn. В частности, пуств в начальный момент времени to для ВСП X(t) заданы вектор математических ожиданий m0 = {moi} = E [X0] , матрица ковариаций
D0 = {Doj } = E [{ X 0 - m 0}{ X 0 - m 0}T ]
и все необходимые начальные моменты ВСВ X 0 до по рядка K.
Задачей исследования является построение системы ОДУ для вычисления математического ожидания mx(t) = {mxi(t)} = E[X(t)], матрицы ковариаций
Dx (t) = {Dxij (t)} =
= E [{ X (t) - m x (t)}{ X (t) - m x (t)}T]
и начальных моментов ВСП X(t) до порядка. K при любом t > tQ.
2. Метод исследования
Для того чтобы получить СОДУ без запаздывания, как и в ряде предыдущих наших работ, применим сочетание метода расширения пространства состояний и метода шагов.
Рассмотрим равномерную временную сетку tq = t0 + q • т. q = 0. 1. 2..... N. ...
и введем новую временную переменную s, изменяющуюся на промежутке [0,т], а также следующие обозначения:
Рассмотрим последовательность полуинтервалов (сегментов) Aq.
На сегменте A0 систему СОДУ для вектора U [0](s) = U 0(s) = col ( Y 0(s), X0(s). Z 0 (s)) представим в виде
Y 0(s) = 0 , Y 0( 0 ) = X 0,
X0(s) = A0(s0) X0(s) + c0(s0) +
+ [®0(s0) : X0(s) + H0(s0)] V 0(s), (2.1)
X 0 (0) = X 0,
Z 0(s) = X 0(s), Z 0(0) = 0 .
Определенный на полуинтервалах A0 и Ai век тор U [1](s) = col ( U [0](s), U i(s)). где U i(s) = col (Yi(s), Xi(s), Z i(s)). будет удовлетворять системе СОДУ (2.1), к которой добавлены уравнения следующего вида:
Y i(s) = 0 , Y 1( 0 ) = Z о(т),
Xi(t) = A(si) Xi(t) + c(si) +
+R(s1) X0(s) + Q(s1) X0(s) +
+ B(si) [Y1(s) + Z i(s) — Z 0(s)] + (2-2)
+ [л(si) : Xi(s) + СД^) : X 0(s) +
+ H(si)] V i(s), X 1 (0)= X 0(т),
Z i(s)= X i(s), Z 1(0)= 0 .
Здесь учтено, что для t G (ti,t2]
t
X(e) de t-τ
t 1
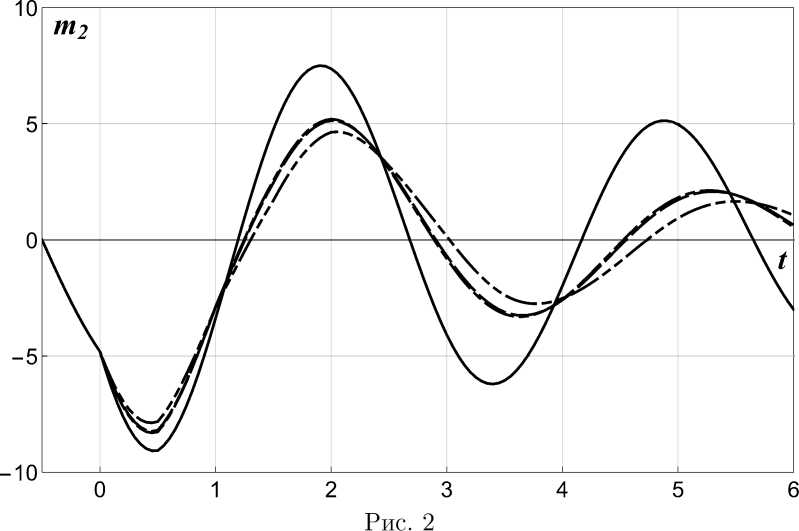
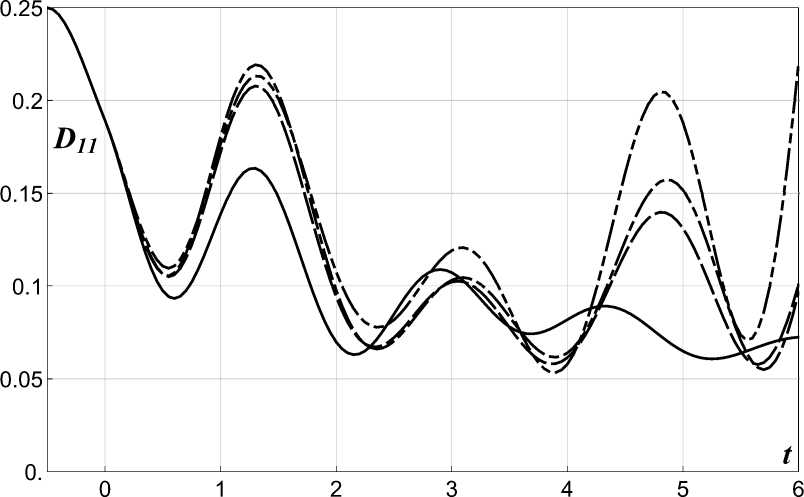
=/X t-τ de + t X(e) t1 dθ sq — s + tq, Aq — (tq, tq+i], X q (s)= X (Sq ), X q (0)= X q-i(T ), V q (S') = V (Sq ), V q (0) = V q-1(T), Zq (s') = s IX q (0) de, 0 Yq (s) ^ Yq = Zq (т), q > 1, col (di, d2,..., dL) = {dll, di2,..., d^, d21 , d22, ..., d2m2, ...,dL1 ,dL2, •••, dLmL }T• t1 X(e) t0 t de + у x (e) de t1 - t-τ X(e) de = t0 ss = z0(т) + у xi(e) de - у x0(e) de = = Yi(s) + Zi(s) - Z0(s). Если обозначить через Un(s) вектор col ( YN (s), X N (s), ZN (s) ), то продолжая подобным образом и далее, находим, что вектор U[N](s) = col ( U[N-i](s), UN(s) ), представляющий поведение ВСП X(t) на сегментах Aq, Ai, ..., An, будет решением системы СОДУ, полученной добавлением к уравнениям для вектора U[N-1l(s) уравнений следующего вида: У N (s) = О, Y N (0) = Z N-1 (т), XN(t)= A(sN) XN(t) + c(sN) + +R(SN) XN-1(s) + Q(sn) XN-1 (s) + + B(sN) [YN(s) + ZN(s) — ZN-1(s)] + + [u(sn) : XN(s) + Q(sn) : Xn-1(s) + + H(sn )] V N (s), X N (0) = X N-1(т), ZN (s)= X N (s), ZN (0)= 0. (2-3) К полученной цепочке систем линейных СОДУ для расширенных векторов состояния U[о]. U[1] U[N]. ... увеличивающейся размерности и подобной структуры без запаздывания при дальнейшем исследовании можно применить стандартные для данного класса уравнений методы [18]. 3. Уравнения для моментных функций Теперь построенную выше на основе разработанной схемы цепочку параметрических линейных СОДУ без запаздывания можно использовать для получения новой последовательности уравнений - последовательности ОДУ для первых и старших моментов векторов Uq. U1 Un- ■■■ я U[0]- U[1U[N ] причем m[k](s) = E [U[k](s)] , D[kl(s) = E [U[kl(s){U [kl(s)}T] = DUoUo(s)DUoU1(s)- DUoUk(s) _ DU1U0 (s)DUiUi(s) ••• DUiUk(s) =, ... ... ... ... .DUkUo(s)DUkUi(s)... DUkUk(s). U[kl(s) = U[kl(s) - m[kl(s), k = 0,1, 2,...,N,... В связи с тем. что при t = s + tk искомые вектор mx (t) = mxk (s) = E [X k (s)] и матрица Dx(t) = DXkXk (s) = = E [{Xk(s)-mXk (s)}{Xk(s)-mXk (s)}T] являются блоками вектора m[k](s) и матриЦЫ D[kl(s) соответственно, необходимо вычислить последние, а затем выбрать из них необходимые элементы. Несложно увидеть, что на каждом этапе k (k = 0, 1, ..., N, ...) после исключения Xk-1 с использованием предыдущих уравнений структура расширенных систем СОДУ принимает следующую форму: U[kl(s) = f [kl( U[kl(s),s) + + G[kl( U[kl(s),s) S[kl(s), (3.1) где U[kl(s) = {Ui[kl(s), i = 14} = = col (Uo(s), U 1(s),..., Uk(s)), f[kl = {fP(U[kl(s),s), i = 14}, i⋆ fF = fff(s) + E fH] (s) Ulkl(s), 1=1 G[kl = {gj, i = ci*,j = 1,j*}, i⋆ gj = gj(s)+E gj(s) Uik(s), 1=1 s [kl (s) = {j (s), j =i,j *} = = col (Vo(s), V 1(s),..., Vk(s)), i* = 3n (k + 1), j* = m (k + 1). Используя компоненты векторов f[kl и матриц G[kl, по формулам Стратоновича [18] мы можем вычислить коэффициенты сноса и диффузии д[kl _ pl , 1 E E dg\k [kl ai = fi ■ 2Ы 2^m[klgji, j=11=1 dUj j⋆ Вik = E g^j ij = 1, 2,...,i*, (3.2) 1=1 уравнения Фоккера-Планка-Колмогорова (ФПК-уравнения) для плотности вероятности вектора U[kl. В свою очередь, на основе этого уравнения может быть построена замкнутая система ОДУ для элементов векторов m[k](s) ii матрип D[k](s) в следующем виде: i⋆ m ak](s) = Е ai E [агk( U [k])a-ei (s)] + i=1 m[k](s) = E [ аг[k]], (3.3) Dg](s) = E[(Ui[k]- mjk]) • ajk] + + (Uj[k]- mjk]) • a'k] + 6^]. (3.4) i⋆ + 2 Е ai (ai - 1) E [6ik (U[k] )a-2ei(s)] + i=1 i⋆ + £ ai aj E [6[k]( U[k^)a-eij (s)] , (3.5 ) i,j=1 К этим уравнениям необходимо добавить начальные условия, форма которых будет такова: m[0](0) = col (m0, m0, 0), где a > 0. ei = {Sij}г*=3. eij = ei + ej. Sj -символ Кронекера. Заметим, что вследствие формы линейных параметрических СОДУ (2.1)-(2.3) для любого |a| > 0 система ОДУ (3.5) будет замкнутой. D[0](0) = 'D0D00' D0D00 0 00 m[k](0) =col (m[k-1](0), mZk-1 (t)> mXk-1 (t)>0), 4. Пример Исследуем характеристики переходного режима, возникающего в системе, которая при t > 0 описывается уравнением X(t) +2 ai X(t) + w2 X(t) + v X(t - т)+ t D[k] (0) = ГD[k-1](0) D^ D^ D^, ■ + 2 a2 X (t — T)+ W2 X (t -T)+e/ t-τ X(0) d0+ D [k] 12 = DUoUk-1 (t ) DUoUk-1 (t ) DUiUk—i (t) + [yi X(t) + Y2 X(t — т) + д] V(t), (4.1) а на полуинтервале (—т, 0] поведение этой системы управляется уравнением .DUk-2Uk-1 (t ). D^ = [DUk-iUo (t) DUk—iUo (t) DUk-iUi (t) ••• DUk-iUk-2 (t)], D2k2]= Duk-iUk-1 (t ). Уравнения для старших моментов СП X(t) можно также получить из соответствующего ФПК-уравнения. Для этого, предва-[k] рительно заменив в коэффициентах aii и 6j К<ШП<)11('11Ты вектора U[k]iia. u[k]. необходимо умножить обе части этого уравнения на (u[k] )а ^ (u1k] )ai (u[k])a2 ... (ui*])ai* (a - мультшшдекс. a = {ai, a2,..., ai*}. |a| = ai + a2 + ... + ai*) и проинтегрировать по пространству Ri*. В результате формально получится следующая бесконечная система ОДУ относительно смешанных начальных моментов: X(t) +2 a0 X(t) + Д X(t)+ +[y0 x(t) + Де] V(t) (4-2) с начальным условием col (X(—т),X(—т)) ~ ~N( col(m0,m0), diag(a0,a0)), (4.3) где ai > 0. wi > 0. v. a2 > 0. w > 0. в- Yi-Y2. Д. a0 > 0. w0 > 0. Y0- Д0 ~ постоянные величины, N(•, •) - нормальное распределение. Если обозначить X(t) через Xi(t), X(t) - через X2(t) П = 2). а V (t) - нс срез V.(t) (m = 1), то, приводя уравнения (4.1), (4.2) к виду (1.1), (1-2), получим, что: A = 0 2 9 , B = 01 01, H = 0 , -w2 -2 ai -в 0 Д R ■ 10 -4» ■ [-"-2 МД ■ И, A = (-Wj -2100] ’ c = c0 = [о] ’ И _ Г [0 11 о _ Г [0 0] [0 0]1 = [[71 0]] ’ ®~ [[72 0]] ’ 0 = [[70 0]] • С использованием разработанной схемы был проведен ряд численно-аналитических расчетов, причем необходимые уравнения сначала генерировались в символьной форме, а затем численно интегрировались стандартными средствами пакета Mathematica. Неизменяемыми данными для этих расчетов были: «1 = 0,1, ^1 = 2,0, «2 = 0,125, ^2 = 1,0, Yi = 0,1, Y2 = 0,05, д = 0,125, «о = 0,125, ^о = 1,5, То = 0,125, до = 0,2, т = 0,5, m0 - [0] ■ D0 - [Т i] • При этом варьируемыми параметрами были v и в, которые принимали следующие значения: 1. v = 0,2, в = 0,125. 2. v = 0,5, в = 0,5. 3. v = 0,5, в = 0,6. 4. v = 0,6, в = 0,5. Результаты расчетов представлены на следующих рисунках: на рис. 1 и 2 - поведение математических ожиданий m1 (t) и m2; на рис. 3, 4 и 5 - изменение компонент Dn (t), D12 (t) и D22(t) матрицы дисперсий. На всех этих рисунках кривые, соответствующие варьируемым параметрам группы 1, изображены непрерывной линией, группы 2 - штриховой (—), группы 3 - штрихпунк-тирной (---) и, наконец, группы 4 - штрих- пунктирной с двумя точками (- • • -). На представленных графиках несложно усмотреть существенную зависимость вычислявшихся моментов от v и в- Заключение В работе представлена схема исследования линейных нейтральных параметрических стохастических интегро-дифференциальных систем с постоянными сосредоточенными запаздываниями. В отличие от известных методов изложенная схема не предполагает предварительного изменения уравнений исследуемого объекта с целью исключения сосредоточенных и распределенных запаздываний или разработки специальных интеграторов. Точность расчетов полностью определяется погрешностью применяемых стандартных процедур численного решения систем ОДУ, причем ошибка метода отсутствует. Заметим, что существует несколько путей повышения эффективности реализации метода в процессе автоматического генерирования уравнений, включая распараллеливание. Рис.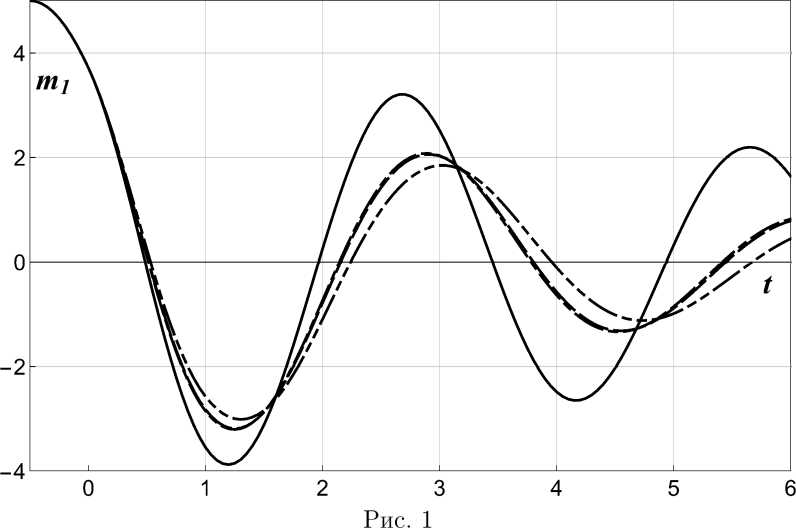
Список литературы К расчету моментных функций решения системы линейных параметрических стохастических интегро-дифференциальных уравнений нейтрального типа
- Азбелев Н.В., Максимов В.П., Рах-матуллина Л.Ф. Элементы современной теории функционально-дифференциальных уравнений. Методы и приложения. М.: Институт компьютерных исследований, 2002. 384 с.
- Беллман Р., Кук К. Дифференциально-разностные уравнения. М.: Мир, 1967. 548 с.
- Хейл Дж. Теория функционально-дифференциальных уравнений. М.: Мир, 1984. 421 с.
- Рубаник В.П. Колебания квазилинейных систем с запаздыванием. М.: Наука, 1969. 288 с.
- Эльсгольц Л.Э., Норкин СБ. Введение в теорию дифференциальных уравнений с отклоняющим аргументом. М.: Наука, 1971. 296 с.
- Bellen A., Zennaro М. Numerical methods for delay differential equations. Oxford: University Press, 2003. 416 p.
- Shampine L.F., Gladwell L, Thompson S. Solving ODEs with Matlab. Cambridge: University Press, 2003. 272 p.
- Erneux T. Applied delay differential equations. New York: Springer-Verlag, 2009. 204 p.
- Рубаник В. П. Колебания сложных квазилинейных систем с запаздыванием. Минск: Изд-во "Университетское", 1985. 143 с.
- Царьков Е.Ф. Случайные возмущения дифференциально -функциональных уравнений. Рига: Зинатне, 1989. 421 с.
- Kushner H.J. Numerical methods for controlled stochastic delay systems. Boston: Birkhauser, 2008. XIX, 281 p.
- Мао X. Stochastic differential equations and applications. Cambridge (UK): Wood-head Publishing, 2011. XVIII, 422 p.
- Mohammed S.-E.A. Stochastic functional differential equations. London: Pitman Publishing, 1984. IX, 245 p.
- Huang C, Vandewalle S. An analysis of delay-dependent stability for ordinary and partial differential equations with fixed and distributed delays//SIAM Journal of Scientific Computations. 2004. Vol. 25, № 5. P. 1608-1632.
- Xu Y., Zhao J. J., Sui Z.N. Stability analysis of ^-methods for neutral multidelay integrodifferential system//Discrete Dynamics in Nature and Society. 2007. Vol. 2007. Article ID 42540. 8 p.
- Makroglou A., Li J., Kuang Y. Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview//Applied Numerical Mathematics. 2006. Vol.56. P. 559-573.
- Huang C, Vandewalle S. Stability of Run-ge-Kutta-Pouzet methods for Volterra integrodifferential equations with delays//Frontiers of Mathematics in China. 2009. Vol.4, № 1. P.03 ST.
- Полосков И.Е. Стохастический анализ динамических систем : монография. Пермь: Изд-во Перм. ун-та, 2016. 722 с.
- Palmeri A., Muscolino G. A numerical method for the time-domain dynamic analysis of buildings equipped with viscoelastic dampers//Structural Control and Health Monitoring. 2011. Vol.18. P. 519 539.
- Белоцерковский СМ., Кочетков Ю.А., Красовский А.А. и др. Введение в аэро-автоупругость. М.: Наука, 1980. 383 с.
- Кхием И. Т. О функции плотности вероятностей процессов, определяемых ин-тегро-дифференциальными уравнениями//Украинский математический журнал. 1983. № 2. С.22Т-234.
- Полосков И.Е. Применение схемы МШ-РФП для анализа линейных стохастических систем с конечными сосредоточенными и распределенными запаздываниями//Вестник Пермского университета. Математика. Механика. Информатика. 2011. Вып. 4 (8). С.53-58.
- Baker СТ., Buchwar Е. Exponential stability in p-th mean of solutions, and of convergent Euler-type solutions, of stochastic delay differential equations//Journal of Computational and Applied Mathematics. 2005. Vol. 184, № 2. P. 404-427.
- Chen C, Tsimin S. Finite element methods for integrodifferential equations. Singapore: World Scientific, 1998. XVII, 272 p.
- Golla D.F., Hughes P. С Dynamics of viscoelastic structures -a time domain, finite element formulation//Journal of Applied Mechanicks. 1985. Vol.52. P.89T-906.
- KhaniA., Moghadam M.M., ShahmoradS. Approximate solution of the system of nonlinear Volterra integro-differential equations//Computational Methods in Applied Mathematics. 2008. Vol.8, № 1. P.TT-85.
- Tari A., Rahimi M. Y., Shahmorad S. et a!. Development of the Tau method for the numerical solution of two-dimensional linear Volterra integro-differential equations//Computational Methods in Applied Mathematics. 2009. Vol.9, № 4. P. 121 135.
- Day J. T. Note on the numerical solution of integro-differential equations//The Computer Journal. 1967. Vol.9, № 4. P.391 395.
- Mehdiyeva G., Imanova M., Ibrahimov V. Application of the hybrid methods to solving Volterra integro-differential equations//World Academy of Science. Engineering and Technology. 2011. Vol.77. P.1083-1087.
- Nguyen H.K., Hergman Т.Е., Cliff EM. Approximations for a class of Volterra integro-differential equations//Mathematical and Computer Modelling. 2005. Vol. 42, № 5 6. P. 659 672.
- Wolkenfelt P.H.M. Modified multilag methods for Volterra functional equations//Mathematics of Computation. 1983. Vol. 40, № 161. P. 301-316.
- Паутов А. С. Численное интегрирование стохастических функционально-дифференциальных уравнений методом Эйлера//Известия Уральского государственного ун-та. 2005. № 38. С. 104 -121.
- Potapov V.D. Nonlinear vibrations and stability of elastic and viscoelastic systems under random stationary loads//Mechanics of Solids. 2011. Vol. 46, № 3. P. 444454.
- Чайковский M.B., Янович Л.А. О численном нахождении корреляционных функций решения систем линейных ин-тегро-дифференциальных уравнений со случайно возмущенной правой частью//Дифференциальные уравнения. 1987. № 2. С. 328-338.
- Chang S.H. On certain extrapolation methods for the numerical solution of integro-differential equations//Mathematics of Computation. 1982. Vol. 39, № 159. P. 165171.
- Lin Т., Lin Y., Rao M., Zhang Sh. Petrov-Galerkin methods for linear Volterra integ-ro-differential equations//SIAM Journal on Numerical Analysis. 2001. Vol.38, № 3. P. 937-963.
- Danfu H., Xufeng Sh. Numerical solution of integro-differential equations by using CAS wavelet operational matrix of integration//Applied Mathematics and Computation. 2007. Vol. 194, № 2. P. 460-466.
- Jalaei K., Zarebnia M., Chalaki M.M. Development of the Sine method for nonlinear integro-differential equations//Australian Journal of Basic and Applied Sciences. 2010. Vol.4, № 11. P.5508-5515.
- Полосков И.Е. Об анализе некоторых классов стохастических интегро-дифференциальных уравнений//Проблемы механики и управления. Нелинейные динамические системы: межвуз. сб. науч. тр./Перм. гос. ун-т. Пермь, 2003. Вып. 35. С. 99-106.
- Полосков И.Е. О расчете первых моментов линейных интегро-дифференциальных систем с параметрическими возмущениями//Проблемы механики и управления. Нелинейные динамические системы: межвуз. сб. науч. тр./Перм. гос. ун-т. Пермь, 2006. Вып. 38. С. 133142.
- Soize С, Poloskov I. Time-domain formulation in computational dynamics for linear viscoelastic media with model uncertainties and stochastic excitation//Computers k, Mathematics with Applications. 2012. Vol.64, № 11. P.3594-3612.
- Karmeshu, Gupta V., Kadambari К. V. Neuronal model with distributed delay: analysis and simulation study for gamma distribution memory kernel//Biological Cybernetics. 2011. Vol. 104, № 6. P. 369-383.
- Hutt A. The study of neural oscillations by traversing scales in the brain: Habilitation 'a diriger des recherches. Universite Nice -Sophia Antipolis, 2011. 102 p.
- Goldfine A. Taylor series methods for the solution of Volterra integral and integro-differential equations//Mathematics of Computation. 1977. Vol. 31, № 139. P. 691707.
- Hu Sh., Lakshmikantham V. Monotone iterative technique for integro-differential equations//Асимптотические методы математической физики: сб. науч. тр./АН УССР. I In-г математики. Киев: 11а-укова думка, 1988. С. 263-270.
- Нгуен В.Д. Асимптотический метод исследования многочастотных колебаний в квазилинейных системах интегро-дифференциальных уравнений второго порядка//Украинский математический журнал. 1977. Т. 29, № 3. С. 404-410.
- Плотников В.А., Рудык О.Г. Об одной схеме усреднения в интегро-дифференциальных уравнениях//Украинский математический журнал. 1989. Т. 41, № 7. С.995-997.
- Филатов А.И. Методы усреднения в дифференциальных и интегро-дифференциальных уравнениях. Ташкент: ФАН, 1971. 282 с.
- Нгуен Т.К. Нелинейные колебания вяз-коупругих пластин под действием стационарных случайных сжимающих сил//Прикладная механика. 1986. Т. 22, № 12. С. 115-118.
- Ariaratnam S.T. Stochastic bifurcation in hereditary systems//8th ASCE Specialty Conf. on Probabilistic Mech. and Structural Reliability. 2000. PMC2000-163. 6 p.
- Xu W., Rong П., Fang T. Duffing oscillator with viscoelastic term under narrowband random excitation//Acta Mechani-ca Sinica. 2002. Vol. 34, № 5. P. 764-771 (in Chinese).
- Brunner H. Collocation methods for Volterra integral and related functional differential equations. Cambridge: University Press, 2004. 597 p.
- Brunner H. High-order methods for the numerical solution of Volterra integro-differential equations//Journal of Computational and Applied Mathematics. 1986. Vol.15. P. 301-309.
- Grossman S.I., Miller R.K. Perturbation theory for Volterra integrodifferential systems//Journal of Differential Equations. 1970. Vol.8. P.457-474.
- Berenguer M.I., Garralda-Guillem A.I., Galan M.R. Biorthogonal systems approximating the solution of the nonlinear Volterra integro-differential equation//Fixed Point Theory and Applications. 2010. Article ID 470149. 9 p.
- Bonilla L.L., bind, A. Relaxation oscillations, pulses, and travelling waves in the diffusive Volterra delay-differential equation//SIAM Journal of Applied Math. 1984. Vol.44, № 2. P.369-391.
- Zhang W. Numerical analysis of delay differential and integro-differential equations: A thesis. St. John's (NL, Canada): Memorial University of Newfoundland, 1998. VIII, 138 p.
- Jokinen O. On non-monotone solutions of an integrodifferential equation in linear vi-scoelasticity//SIAM Journal of Numerical Analysis. 1996. Vol.33, № 4. P. 1410-1424.
- Houwen P.J. van der, Sommeijer B.P. Eu-ler-Chebyshev methods for integro-differential equations//Applied Numerical Mathematics. 1997. Vol.24, № 2-3. P. 203218.
- Полосков И.Е. Расширение фазового пространства в задачах анализа дифференциально-разностных систем со случайным входом//Автоматика и телемеханика. 2002. № 9. С. 58-73.
- Полосков И.Е. Движение транспортного средства по дороге со случайным профилем с учетом запаздывания//Математическое моделирование. 2005. Т. 17, № 3. С. 3-14.
- Полосков И.Е. Компьютерное моделирование динамики загрязнения бассейна реки с учетом запаздывания и случайных факторов//Вычислительные технологии. 2005. Т. 10, № 1. С. 103-115.
- Полосков И.Е. Схема метода расширения фазового пространства для анализа линейных параметрических стохастических систем с кратными запаздываниями//Вестник Пермского университета. Математика. Механика. Информатика. 2007. Вып. 7 (12). С. 26-30.
- Poloskov I.E. Symbolic-numeric algorithms for analysis of stochastic systems with different forms of aftereffect//Proc. in Applied Mathematics and Mechanics (PAMM). 2007. Vol.7, № 1. P.20800112080012.
- Полосков И.Е. Анализ линейных стохастических систем с запаздывающим аргументом нейтрального типа//Вестник Пермского университета. Математика. Механика. Информатика. 2010. Вып. 2 (2). С. 61-66.
- Malanin V. V., Poloskov I.E. About some schemes of study for systems with different forms of time aftereffect//Proc. of the IUTAM Symp. on Nonlinear Stochastic Dynamics and Control/W.Q.Zhu, Y.K. Lin, G.C.Cai (eds.). IUTAM Bookseries, Vol.29. Dordrecht: Springer, 2011. P. 5564.
- Malanin V. V., Poloskov I.E. On some methods for study of stochastic hereditary systems//Procedia IUTAM. 2013. Vol.6. P. 60-68.
- Полосков И.Е. Схема расширения вектора состояния для решения интегро-дифференциальных уравнений в частных производных//Вестник Пермского университета. Математика. Механика. Информатика. 2013. Вып. 2 (21). С. 59-65.
- Полосков И.Е. Применение схемы МШ-РПС для анализа линейных стохастических систем с распределенными и конечными сосредоточенными запаздываниями//Вестник Пермского ун верситета. Математика. Механика. Информатика. 2014. Вып. 4 (27). С. 68-77.
- Полосков И.Е. Об одной численно-аналитической схеме расчета первых моментных функций вектора состояния линейной стохастической интегро-дифференциальной системы//Вестник Пермского университета. Математика. Механика. Информатика. 2015. Вып. 2 (29). С. 52-62.
- Полосков И.Е. Анализ линейных стохастических интегро-дифференциальных систем с сосредоточенными запаздываниями//Вестник Пермского университета. Математика. Механика. Информатика. 2016. Вып. 2 (33). С. 98-105.
- Poloskov I., Malanin V. A scheme for study of linear stochastic time-delay dynamical systems under continuous and impulsive fluctuations//International Journal of Dynamics and Control. 2016. Vol.4, № 2. P. 195-203.
- Mangano S. Mathematica cookbook. Se-bastopol: O'Reilly, 2010. XXIV, 800 p.
- Smith H. An introduction to delay differential equations with applications to the life sciences. New York: Springer, 2011.


