К вопросу о совпадении гильбертовых пространств, интегрируемых с квадратом по мере функций

1.    Введение. Постановка задачи

Многие задачи комплексного анализа, такие как интерполяция аналитических функций, вопросы уравнений свёртки, вопросы базисности, полноты определенных систем функций сводятся к изучению свойств конкретных гильбертовых пространств с воспроизводящим ядром. Данная работа, посвящена, изучению вопроса: какие условия гарантируют

совпадение гильбертовых пространств с воспроизводящим ядром? Пусть Н - некоторое гильбертово пространство с воспроизводящим ядром, состоящее из функций, заданных на множестве П С С^п, п >  1, т.е. функционал 5^, ставящий в соответствие любой функции f € Н значение функции f в точке £ € П, является линейным и непрерывным функционалом над Н для произвольной точки £ € П. Предположим, что {e1(> £)}GQ1, {e2 (•, £) }^_Gm -некоторые полные системы функций в Н, Пі С C^m, m ^ 1. Обозначим

f(z) =' (ei(;z),f )н Vz € П1, Н = {f,f € Н },

(f1,f2)H = (f2,f1)H, Шн = Ш\Н Vf1, f2 € Н, jV) d= (e2(;z),f)h Vz € П1, Н = {f,f €Н},

(fl^H = (f2,f1)H, IMh = Шн Vfif €Н .              (1)

Необходимо наити условие, при выполнении которого пространства Н и Н совпадают, т.е. Рт Рт

Н и Н состоят из одних и тех же функции, и

If \н = If ІН Vf €Н = Н.

Также изучается вопрос: при каких условиях пространства Н и Н эквивалентны, т.е. Н л Н состоят из одних я тех же функций. и нормы \| • \\н II • ІІН эквивалентны. Ранее в работе [1] было введено определение согласованности двух систем функций с некоторым оператором Т : Н ^ Н.

Определение 1. Системы функций {ej ( • ,z ) } _zG q ₁ , j = 1, 2, принадлежащие гильбертову пространству Н, навиваются согласованными с оператором Т : Н ^ Н, если выполнено соотношение:

(ei(^, zi), 62(3 Z 2 )) h = (ei(•, Z2), Т 62(3 zi))_H Vzi, Z2 € Пі. (2)

В [1] доказано, что если пространства Н, Н совпадают (эквивалентны), то системы функций {ej ( • ,£ ) } § _G q ₁ , j = 1, 2, являются согласованными с некоторым линейным непрерывным взаимно однозначным унитарным (неунитарным) оператором Т : Н ^ Н. Также если системы функций {ej ( • ,£ ) } § _G q ₁ ,j = 1, 2, являются ортоподобными системами разложения (определение см. [2]) в пространстве Н с одной и той же мерой ц, заданной на Пі, и выполнено условие согласованности с некоторым линейным непрерывным обратимым оператором Т: Н ^ Н, то пространства Н, Н совпадают или эквивалентны. Также построены примеры, в которых условие согласованности выполнено, однако пространства не совпадают (не эквивалентны). В этой работе мы доказываем, что если системы функций {ej ( • ,£ ) } § _G q ₁ , j = 1, 2, являются ортоподобными системами разложения в пространстве Н с разными в определенном смысле мерами ц1. ц₂. то и пространства Н. Н не равны. Таким образом, в этом случае из условия согласования ортоподобных систем не следует совпадение (или эквивалентность) пространств Н и Н.

Также в этой работе доказано утверждение о том, что из условия согласования двух полных в Н систем <1 іуіікпнн {ej(•, z)}_zGQ1 , j = 1, 2. вытекает, нто оператор В. опреле.теппый из условия

В: ei(^,^)^ e2(;^) V^ € Пі, с областью определения span{e1(^,^)}^GQ1, допускает расширение до замкнутого оператора.

Далее в статье рассмотрен вопрос о совпадении пространств сужений функций из гильбертовых пространств с воспроизводящим ядром. Полученные результаты проиллюстрированы на примере конечномерного пространства C2.

2.    Основные результаты

Заметим, что задачу о совпадении гильбертовых пространств с воспроизводящим ядром можно было бы сформулировать следующим образом. Рассмотрим два гильбертовых пространства с воспроизводящим ядром Hi и Н2. состоящие из функций, заданных на некотором множестве точек Qi С C^m, m ^ 1. При каких условиях эти пространства совпадают (эквивалентны), т.е. состоят из одних и тех же функций и нормы этих пространств равны (эквивалентны) ||f||ні = ||f||н Vf € Hi = Н₂. (|f||ні ~ ||f||н V f € Hi = Н2)?

Приведенная в введении формулировка задачи по сути эквивалентна последней формулировке, поскольку, например, в случае сепарабельности пространств Hi, Н2 в качестве пространства Н можно взять пространство «коэффициентов» разложения фуикщш из Hi 11 Н2 по ортоиормироваппым базисам в Hi 11 Н2 соответствешю. Пространство Н в этом случае есть пространство І2 и состоит из последовательностей комплексных чисел, сумма квадратов модулей которых конечна. Последовательности функций от переменной 2 € Qi {ej(k, г)}^, 2 € Qi, j = 1, 2, являются ортонормированными базисами в пространстве Hj , j = 1, 2, соответственно. Таким образом, справедливы представления функций из пространств Hi 11 Н2:

∞

/ (2) = ^U,ei(k, ^щ. ei (k^) V2 € Qi Vf € Hi, k=0

∞

9(2) = ^(g,e2(k, ^нe2(k,z) Vz € Qi Vg € H2.

k=0

Семейства последовательностей {ej ( • ,2 ) } _zG q ₁ ,j = 1,2, принадлежат пространству 12. Положим Н = 12. Для этого случая рассмотрим пространства Н и Н (см. (1)). Из теоремы 1 работы [3] вытекает, что Н = Н1, Н = Н₂.

Для формулировки основного результата необходимо дать следующее

Определение 2. Пусть Н - гильбертово пространство с воспроизводящим ядром, состоящее из функций, заданных на Q. Q - пространство с мерами ц1 и ц2. Меры ц1 и ц2 назовем Н - равными, если для любых функций f € Н выполнено соотношение j |f (2 j 2 А//_ мз) = j|f (z)|2 dp2(z) < то.(4)

В связи с данным определением приведем следующий пример. Рассмотрим пространство Пэли - Винера, состоящее из целых функций F (2), 2 € C типа не выше а >  0 таких, что для сужения на вещественную ось этих функций выполняется оценка

\F\pWa = /    |F (x)|2dx = [ |F (х + Д)|2^х 0 5(y)dy < то,(5)

-∞C

( [4], с. 25-26). Пространство PW_a - гильбертово пространство с воспроизводящим ядром

^KPW_a^(2,С) =

sin а(2 — |) ^С^{2 —} Д

2,^ € C

(см, например, [4], с. 3-7).

Система воспроизводящих ядер {Kpw_a(2, ^)}+=—_го будет ортонормированным базисом в пространстве PW_a. По сути этот факт составляет содержание известной теоремы Котельникова. Согласно равенству Парсеваля

\F \Pw_a

ТС

а

+∞

∑︁ k= '^

F (-)  .

а

Равенства (5),(6) означают, что меры dx®5(y)dy и ^+=— ^ ^ -5 _Тк являются PW_a - равными.

Нам понадобится следующая

Лемма 1. Пусть пространство Н состоит из функций, заданных на множестве Q1. Пусть на Q1 заданы дес счстно-консчныс меры ц1. ц₂. Система функций {e1(-,^)}^_GQ1 является ортоподобной системой разложения с мерой ц1 в пространстве Н. Тогда следующие условия равносильны:

• 1)    Меры ц1. ц₂ являются Н-равными мерами:

• 2)    Система функций {ет(-, ^)}^_е^_т является ортоподобной системой разложения с мерой ц₂ в пространстве: Н.

Доказательство. Докажем необходимость. Так как меры ц1, ц₂ являются Н-равными, то для любой / Е Н справедливо равенство

II/ \\H = I/I h =     \/(z)\2d_№(z)= / \/(z)\² dp2(_Z) <  TO.

J Qi                      Qi

Отсюда, учитывая, что /(z) = (e1(-,z),/ )_Н Vz Е Q1 V/ Е Н. следует равенство

11^/\Н = 1 \^(/,ei⁽-^,z))H \2^d№^{(z) V/ Е Н}.

Ω1

Применяя результат из работы [2, теорема 11], мы получим, что система функций {ei (•, ^) } ^ g Q i является ортоподобной системой разложения с мерой Ц2 ^в пространстве Н. Необходимость доказана.

Докажем достаточность. Предположим, что система функций {ei(•, ^)}^_eQ_T является ортоподобной системой разложения с мерой ц₂^в пространстве Н. По условию леммы эта же система функций {ei(-,£)}§_GQ1 является ортоподобной системой разложения с мерой ці в пространстве Н. Тогда, согласно аналогу равенства Парсеваля для ортоподобных систем разложения [2, теорема 1], выполняется равенство

II/\Н = 1 \(/,ei(-,z))H \² dm(z) = / \(/,ei(-,z))H \² d^(z) V/ Е Н.         (7)

Ω1                               Ω1

Отсюда, учитывая, что для любой һ Е Н найдется Д Е Н такая, что h(z) = (ei(•, z), /ң)н Vz Е Qi, из равенства (7) следует, что для любой функции һ Е Н справедливо равенство

J \h(z)\² d^1(z) = j \h(z)\² d^₂(z) < то.

Таким образом, меры ц1 и ц2 являются Н-равными. Лемма 2 доказана.

Сформулируем и докажем необходимое условие совпадения пространств Н и Н.

Теорема 1. Пустъ {e1(-, z)}_zGQ1, {e₂(-,z)}_zGQ1 — две ортоподобные системы разложения в гильбертовом пространстве Н с мерами ц1, ц₂ соответственно. Пространства Н и Н совпадают тогда и то.нъко тогда, когда, .меры ц1. ц₂ будут Н-равны или Н-равны, и найдется линейный непрерывный обратимый оператор Т, осуществляющий изометрию пространства Н такой, что системы функций {ej(-,z)}_zGQ1, j = 1, 2, согласованы с оператором Т, т.е. выполняется соотношение (1).

Доказательство. Докажем необходимость. По утверждению 1 статьи [1] из совпадения пространств Н, Н следует условие согласования, т.е найдется линейный непрерывный взаимно однозначный унитарный оператор Т : Н ^ Н такой, что

(ei(-,zi),e2(-,z2))H = (ei(-,z2), Т e2(-,zi))_H Vzi,z2 Е Qi.

Из равенства (8) вытекает равенство mm

(У^ ckei(-,zk),е2(-,£))н = У" ckТe2(^,zk),ei(л-А^н VE € Qi•(9)

k=1k=1

Здесь {z_k }k=i ^— произвольный набор точек из Qi, a {ck}m=i ^— произвольный набор комплексных чисел. Пусть p(t) ^d= ^m=i Ckei(t, Zk ), t E Q, - произвольная функция из линейной оболочки системы функций {e^, z)}_zGQ1, и q(t) ^d= ^m==₁ CkТ e₂(t,Zk), t E Q, - функция из линейной оболочки системы функций {Т e2^, z)}_zGQ1. В этих обозначениях равенство (9) записывается следующим образом:

⁽p⁽•^{), e}2⁽a ^Е))н = (q^Hi^E^н V£ ^{E Q}i.

Заметим, что система функций {Т e2(•, E)}^_G^1 также ортоподобная система разложения с мерой Ц2 в пространстве Н, поскольку оператор Т : И ^ И унитарный и система функций {e₂(•, Е)}$eQ1 ~ ортоподобная система разложения с мерой ц₂ в пространстве Н.

Так как пространства Н, Н совпадают то, согласно [5], существует линейный непрерывный взаимно однозначный унитарный оператор А : Н ^ Н, обладающий свойством

А: e1(•,z)^Тe2(>z) Vz E Qi и А: p ^ q. Но тогда в с илу того, что {ej (•,z)}zGq1 ,j = 1, 2, - ортоподобные системы разложения в пространстве Н, учитывая равенство (9), а также то, что меры №,№ будут Н-равны, получим соотношение

I \(p,e2(;E))H\²dp2(E) = \\p\\H = WAp\\H = \\q\\H =

Ω1

= / \⁽q^,ei(-^,E )) h \2dm^(E)=l \⁽p^,e2⁽^^,E))H \2dm^(E). Ω1                                Ω1

(Ю)

Заметим, что пространство H можно определить как пополнение семейства функций

S = {p'(z) = (e2(^,z),p)H z E Qi, p E spon{ei(^,z)}zGQi}, относительно нормы

HpIIh =

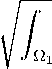
\p(z)\2 dMz).

Также мы можем определить пространство Н і как пополнение семейства функции

{p(z) d= (e2(^,z),p)H, z E Qi, p E span{ei(^,z)}ZGQi}, относительно нормы

\p\h₁ = \ /   \p(z)\2dpi(z).

1         Ω1

В силу равенства (10) пространство Н₁ определяется корректно. Более того, можно сказать, что пространства Н и Н₁ совпадают, т.е. состоят из одних и тех же функций и нормы в пространствах Н и Н₁ совпадают. В самом деле, докажем, что если последовательность (руикщш {т_п }п^о С S сходится по порэю пространства. || • \н ^{к пекото}Р°й <1>упкщш / E Н. то / E Н₁ и {г_п}_п^о сходится к / по норме \ • Ннр Действительно, согласно (10), справедливо равенство

I \r_n^(z)\^{2 d}pi^(z) = \rn\23 .

Ω1

Поскольку пространство Й - гильбертово пространство с воспроизводящим ядром, последовательность функций p_n(z) сходится при любом фиксированном z Е Qi к некоторому значению /(z); поэтому последовательность y_n(z) = |r_ra(z)|² сходится при любом z Е Qi к |/(z)|². Отсюда вытекает, что для любого е > 0 найдется N_e такое, что

/ y_n^(z)dpi^(z) ^ II/Н²^ + Е, п ^ ^N_e.

Ω1

Согласно теореме Фату (см., например, [6], с. 305), функция |/(z)|, z Е Qi интегрируема по Лебегу, и в силу того, что е произвольно, получаем оценку

I |/(z)|²dm(z) ^ Н/ Нй V/ еН .

Q1                        "

Докажем, что

/ |/ (z)2 dpi(z) = Н/ Нй V/ ЕЙ .

Ω1

Обозначим u(/) ^ Н/\\H, / Е Й и v(/)=f I|/(z)|2d№(z),   / ЕЙ.

В силу неравенства треугольника

v(/ ) <  v(/ — д) + v(д) V/,д ЕЙ,

^u(/) < ^{u(/ -} д⁾⁺ и⁽д) ^,д ^ЕЙ. (11)

Отсюда

W )- <д)1 д) ^/,д ей,

^|u(/) -Цд) ^^u(/ - д) ^,д ^ЕЙ. (12 )

Поэтому отображения u, v : Й ^ R непрерывны. Равенство (10) означает, что непрерывные отображения u и v совпадают на всюду плотном в Й-множестве. Следовательно, u(/ ) = v(/ ) V/ Е Й. Таким ооразом.

^Н/НН = \ / ^{|/ (z})^{l d}^2^(z) = \ / ^{l/ (z)|}2 dpi^{(z) V/ ЕЙ}. Ω1                         Ω1

Значит, меры ц1 н ц₂ будут НТ-равны пли. что то же самое. Н-равны.

Для доказательства достаточности условий теоремы воспользуемся леммой 1. Согласно этой леммы, если меры ц1 и ц₂. например. Н-равны. то снетема (рупкщш {е1(^, /)}^_GQ1 является ортоподобной системой разложения не только с мерой ці, но и с мерой й2. По условию теоремы система функций {в2 (•,/)}§eQ₁ является ортоподобной системой разложения с мерой Ц2 в пространстве Й. Учитывая это замечание, далее доказательство достаточности условий теоремы 1 повторяет доказательство утверждений 3, 4 работы [1]; в пространстве Й системы функций{еу(•,/)}§eQ₁ , 3 = 1, 2, - ортоподобные системы разложения с одной и той же мерой Ц2. Теорема 1 доказана.

Пусть {еу(•,/)}§eQ1, 3 = 1,2, - две полные системы функций в гильбертовом пространстве Й. Если системы функций {еу(•,/)}§eQ1, 3 = 1,2, согласованы с некоторым линейным непрерывным взаимно однозначным оператором Т, то оператор В, который переводит систему функций {еі(^,/)}^GQ1 на {б2(^,/)}^GQ1, не обязан продолжаться до линейного непрерывного взаимно однозначного оператора. Однако условие согласования гарантирует, что оператор В, определенный на линеале зратДеіф ,£)}gGQ1, будет иметь замкнутое расширение. В связи с этим докажем следующее:

Утверждение 1. Пусть { ej ( • ,£ ) } § _g q ₁ ,j = 1,2, - две полные системы функций в гильбертовом пространстве Н. Если системы функций { ej ( • ,£ ) } § _g q ₁ , j = 1, 2, согласованы с некоторым линейным непрерывным обратимым оператором Т, то линейный оператор

В: еіДД^ e2(;O,  £ е Иі, определенный на линейной оболочке системы функций {e1(> Д}£ею1, допускает расширение до замкнутого оператора.

Доказательство. Пусть ж",п е N - последовательность из 8рап{е1ф, £) } $eQ1 ж" ^ ж, ж е Н и В ж" ^ у’, у’ е Н, и ж", п е N - последовательность из span { e1( ^ ,£) } g_GQ1 ж" ^ ж, ж е Н 11 В ж" ^ у”. у” е Н.

Из условия согласования, пользуясь непрерывностью скалярного произведения, получаем

(у’^ДД^н = ( lim ^ДщфД^н = "^^

= Нт (Б^еД-ДДн = lim (ж",Т^СД^Н = "^^"^^

= ( lim ж", Те2^ Д^н = ( lim ж", Т*e2G,£))Н = "^^"^^

= lim (ж", Т*в2(-,£))н = lim (Вж", еі(-,£))н = п^^"^^

= ( lim В ж" ,еі(;£))_н = (у",еі(^,£))_н W е И_ь п^^

Тогда

⁽у’ ^- у”, ^еДД))н = 0 V ^{£ е И}і.

Из полноты системы функций {еіД ДДею1 в пространстве Н следует, что у’ = у’’, значит, оператор ж н- Вж определяется однозначно, т.е. оператор В допускает замкнутое расширение. Утверждение 1 доказано.

Рассмотрим построенные в статье [1] примеры, когда выполнено условие согласования ортополобных систем {ej ( • ,z ) } _zG q ₁ , j = 1, 2. но пространства Н. Н нс совпадают. Мы (фактически доказали, что в этих случаях линейный оператор В:

В: ex(^,^) н- e2(>z) Vz е Иі, который определен на линейной оболочке системы функций {еД-, z)}zGQ1, не может быть продолжен как линейный непрерывный взаимно однозначный унитарный оператор, действующий из Н на Н. Действительно, еели бы оператор В продолжался до линейного непрерывного взаимно однозначного оператора, осуществляющего автоморфизм пространства Н, то пространства Н и Н совпадали бы. Но в построенных в [1] примерах - это не так. Значит, в этих случаях, оператор В не может быть продолжен как линейный непрерывный взаимно однозначный унитарный оператор, действующий из Н на Н и, так как условие согласования выполнено, то по Утверждению 1 оператор В продолжается до замкнутого оператора с некоторой плотной в Н областью определения, оператор В-1 также имеет замкнутое расширение, оператор В* определяется корректно. Поэтому

(еі( ^ ,2і),е2( ^ ,22))н = ( В -^Дщ), В еі( ^ ,^2))н =

= ( В * оВ ^-іе2( ^ ,2і),еі( ^ ,22))н = (еі( ^ ,^2), В* о В —^Д £і))_н V^,^ е Иі.       (13)

С другой стороны, выполнено условие согласованности:

(е іД гД^Д^Дн = (ві( ^ , Z2), Т е2Дщ))_н  V^,^ е Иі.

Из соотношений (13), (14) вытекает, что оператор В* о В ¹ в данном случае будет продолжаться до линейного непрерывного взаимно однозначного оператора Т, действующего из Н на. Н .

Далее мы рассмотрим вопрос о совпадении гильбертовых пространств сужений. Пусть Q0 С Qi- Мы также предполагавм, что системы функций {ej ( • ,z ) } _zG q ₀ ,j = 1, 2, полные системы в пространстве Н. Пространство Н ⁰ состоит из всех сужений функций из про-страпства. Н на подміюжество Q0 ооласти опрелелепия Qi. прострапіство Н ⁰ состоит из всех сужений функций из пространства Н на подмножество По области определения Q_i. При этом

1/«й0 “= II/Лй V/е Н , Ыйо"^ Н а Н й ^v9 ей .

Следующее утверждение по сути есть частный случай утверждений 1, 2 статьи [1].

Утверждение 2. Если пространства Н ⁰ и Н ⁰ совпадают (эквивалентны), то найдется линейный непрерывный взаимно однозначный унитарный (неунитарный) оператор Т : Н ^ Н такой, что выполнено соотношение

(еі(^,гі),е2(^,22))й = (ei(-,z2), Т е2фщ))_й Vzi е Q0Vz2 е Q0.             (15)

Доказательство. Повторяется доказательство утверждения 1 и утверждения 2 работы [1]. Справедливо также следующее утверждение

Утверждение 3. Пусти меры ортоподобных систем ej (•, z), z е Qi будут Н-равны или Н-равны. Если найдется линейный непрерывный взаимно однозначный унитарный (неунитарный) оператор Т : Н ^ Н такой, что выполнено соотношение

(еі(^,гі),е2(^,22))й = (еі(^, 22), Тe2(•,Z1))_Й Vzi е Q0Vz2 е Qi,

то пространства Н ⁰ и Н ⁰ совпадают (эквивалентны).

Доказательство. Доказательство проводится по схеме из [1]. Равенство (16) влечет соотношение тт

(^ Ckei(^, zk),в2(-Д))й = (^ СкТe2(-,zk), ei(•,О)й V^ е Qi.(17)

k=ik=i

Здесь {zk }m=i ^— произвольный набор точек из Q0, а {ск }m=i ^— произвольный набор комплексных чисел. Пусть p(t) "= ^k=i Скei(t, Zk ), t е Q - произвольная функция из линейной оболочки системы функций {ei(-, z ) } _zG q₀, и q(t) "= ^k=i CkТe₂(t,z_k ), t е Q - функция из линейной оболочки системы функций {Т е2ф z ) } _zG q₀. Пусть, согласно условию, меры pi и р₂ являются либо Н-равными, либо lf-равными. Предположим, для определенности, что меры p_i 11 p₂ будут Н-равны. Тогда, согласно лемме 1. система функций {e_i(-, z)}_zGQ1 является ортоподобной системой разложения с мерой р2- Функции p, q принадлежат пространству Н, системы функций {ej(•, z)}_zGQ1 , j = 1, 2, - ортоподобные системы разложения с мерой р2 в пространстве Н. поэтому

P^(t) = I ⁽Р^,е2⁽^^,С⁾⁾Й^e2^(t,^) dp2⁽<) ^{Vt е Q},

Ω1

q(t) = / (q,e1(•,^))й ei(t,0 dp2«) Vt е Q.

Ω1

В силу аналога равенства Парсеваля [2, теорема 1] и соотношения (17) справедливо равенство

«Р«Й = /’ l(p,e2U))l²dp2«) =

Ω1

= / l(q,eiU))l²dp2«) = 1q1Й

Ω1

или ||р||п = ||q||n- Определим оператор А по следующему правилу: А: р н- q. По теореме Банаха [7, с. 240, теорема 2] А продолжается до линейного непрерывного взаимно однозначного унитарного оператора, действующего из Н в Н. Тогда оператор А1 = Т ^-1 о А — изометрия пространства Н и А1: еД> Д Н- е₂(-,£) V£ € По- Применяя [5, теорема 1], мы получаем, что Н ⁰ = Н 0. Утверждение 3 доказано.

3.    Пример

Приведем пример, иллюстрирующий утверждения 2, 3. В качестве пространства Н возьмем пространство C². Рассмотрим следующий набор векторов в пространстве C²:

е1 = (1, 0),  е2 = (0,1), е3 = (^, ^),  е4 = (^, -^).

Далее определим наборы векторов {е1Дк)}4=1 и {е₂ ДкуД^, в пространстве C²:

е1(ч 1) := -1 • е1, е1(ч 2) := -1 • е2, еі(^, 3) := -г • е3, еі(^, 4) := -г • е4;

е2(-, 1) := г • е1, е2(-, 2) := г • е2, е2(Ч 3) := е3, е2(3 4) := е4.

Зная наборы векторов {е1Д к)}4=1 и {е₂Д к)}4=1, мы определим пространства Н, Н. В данном случае Н = C², и пространства Н и Н будут состоять из 4-мерных векторов {/(к)}.=1 и {/(к)}4=1 соответственно. Здесь

Дк) =' (еД - .к),/ (Д)п,   / ЕН, к = 1, 2, 3,4;

7(к) = (е2( ^ ,к),/ (Д)п,   / ЕН, к = 1, 2, 3,4.

При этом, согласно определению векторов {еД-, к)}|=1 и {е2(-, к)}.=1, учитывая равенство Парсеваля, можно вычислить

,  ~       Л       ~       л                <---^-^

({У^1(к)}4=1, {У^2(к)}4=1)п = 2 Е /1(к) • ./^2(к),(18)

4 4=1

({.Д(к)}4=1, {.^(к)}4=1)п = 2Е-Ык) •■/2(к).(19)

4=1

Следует отметить, что нормы векторов {/(к)}4=1 и {₁/^(к)}4=₁ совпадают. Однако эти векторы разные, поэтому пространства Н, Н не обязаны совпадать. Рассмотрим теперь пространства Н ⁰ и Н 0, которые состоят из 2-мерных векторов {/(к)}4=1 и {/(к))4=1 соответственно. Здесь

У^(к)⁽=^/ (е1( ^ ,к),/ ( ^ ))п,   / ЕН, к = 1, 2;

Дк)^ (е2( ^ ,к),/ ( ^ ))п,   / ЕН, к = 1, 2.

При этом, согласно определению векторов {е1(^, к)}4=1 и {е2(^, к)}4=1, учитывая равенство

Парсеваля, можно вычислить

(^{/1^(к)}4=1, ^{/2^(к) } 4=1)т70 = Е^1^(к) ^ ^2^(к), 4=1

({Л (к) } 1 ₌₁ , ШкДк^п 0 = Е-^ (к) •№) 4=1

Ниже приведены выражения для скалярных произведений векторов {еД-, k)}£=1 и

{e2(^,k)}Lr	Знак id обозначает тождественный оператор.
	(е1Д 1), e2(M 1))H = (е1Д 1), —г^[е2(-, 1)])h , (е1Д 1), e2(G 2))H = (e1(O 2), —г^[е2(-, 1)])h , (e1G, 2), e2(G !)) h = (e1(O 1), —г^[е2(-, 2)])H, (e1G, 2), e2(G 2))H = (e1(O 2), —г^[е2(-, 2)])H.	(20)
И далее	(e1G 1), e2(-, 3))H = (e1(H 3), 2d[e2(>1)])H, Ha 1),e2(, 4)) h = (еД*, 4),гф2Д 1)]Д , (e1G 2),e2(3 3))H = (e1(H 3),г^[е2(> 2)])h , Ha 2),e2(^, 4)) h = Ha 4),гф2Д 2)]Д.	(21)
Однако	(e Д •, 3), e2(G 3))H = (e1G, 3), —г^[е2(^, 3)])h , (e1(., 3),e2(^, 4)) h = (еДн 4), —zd[e2(^, 3)]) h , (e1(^, 4), e2(H 3))H = (e1(H 3), —г^[е2(^, 4)])H, (e1(., 4),e2(., 4)) h = (еДн 4), —id[e2(-, 4)]) h .	(22)

В сотношениях (20) - (22) присутствует как оператор умножения на —1, так и тождественный оператор. Но не существует линейного непрерывного взаимно однозначного унитарного оператора Т, действующего из Н в Н такого, что системы векторов {ej(•, k)})(=1, j = 1, 2, были бы согласованы с оператором Т, т.е. было бы справедливо соотношение (2)

(ei(;k^,e2(;V)b = (ei(;l), Тe2(;k)) _H Vk, l G {1, 2, 3,4}.

Легко видеть, что пространства Н⁰ и Н⁰ совпадают. Это можно увидеть также из соотношений (20), которые означают, что системы векторов ei(^,k) и e2(^,k) к = 1, 2, согласованы с оператором умножения на число —1. Однако пространства Н и Н не совпадают. Действительно, согласно результату из [5], если бы пространства Н и Н совпадали, то нашелся бы линейный непрерывный взаимно однозначный унитарный оператор Л : Н ^ Н, такой что

Л: e₁(^,k) ^ e₂(-,k), к = 1, 2, 3,4.

Однако такого оператора не существует. Действительно, заметим, что наборы векторов {e1(^,k)}2=1 и {e2(^,k)}2=1 и {ei(-,k)}^=3 и {e2(-,k)}^=3 являются ортонормированными базисами в пространстве C2. Оператор Л (если он существует) полностью определяется своим действием на базисе. Из условия

Л: e1(-,k) ^ e2(-,k), k = 1, 2

следует, что оператор Л есть оператор умножения векторов из C² на число —г. Условие

Л: еД^Д) ^ e₂(>k), k = 3, 4

влечет, что оператор Л есть оператор умножения векторов из C² на число г. Но не может существовать линейного непрерывного взаимно однозначного унитарного оператора Л: Н ^ Н. который одновременно был бы и сшератором умножения векторов п:з C² на число —г и оператором умножения векторов из C² на число г. Получаем противоречие.

Значит, не существует линейного непрерывного взаимно однозначного унитарного оператора, Л: Н ^ Н такого, что

Л: еД-Д) ^ e2(-,k), k = 1, 2, 3,4.

Поэтому пространства Н и Н в данном примере не совпадают.