К вопросу о способах активизации учебно-познавательной деятельности студентов вузов
Автор: Гуменникова Ю.В., Черницына Р.Н., Узденова М.Б.
Рубрика: Педагогические науки
Статья в выпуске: 5 (104) т.27, 2025 года.
Бесплатный доступ
Необходимость подготовки специалистов с высоким уровнем профессионализма требует разработки методов и средств обучения, обеспечивающих формирование компетентности будущих инженеров, в том числе активизации учебно-познавательной деятельности студента, показывает актуальность разработки форм и способов такой активизации. В данной работе авторы рассматривают один из возможных методов активизации учебнопознавательной деятельности студентов вуза, для чего она разделяется по уровням: отражение, осмысление, алгоритмирование и контролирование; описывают психологические процессы, реализуемые на каждом из них. На всех уровнях познавательной деятельности происходит последовательное перемещение по этапам: узнавание, воспроизведение, применение и творчество. Таким образом, процесс усвоения учебного материала можно представить матрицей размерностью 4 4 . В работе показывается организация учебно-познавательной деятельности обучающегося на первом (элементарном) уровне, где на этапе узнавания происходит перемещение от отражения к контролированию. Приведен пример математической задачи раздела «Аналитическая геометрия» первого уровня сложности, решение которой состоит из четырех учебных компонентов. Предложенный подход дает возможность объединить учебный материал в общую систему, распределив его по четырем уровням соответственно степени сложности заданий.
Учебно-познавательная деятельность, познавательная активность, познавательно- деятельностная матрица, уровень сложности, математическая задача, учебный материал
Короткий адрес: https://sciup.org/148332368
IDR: 148332368 | УДК: 378.147 | DOI: 10.37313/2413-9645-2025-27-104-3-8
Текст научной статьи К вопросу о способах активизации учебно-познавательной деятельности студентов вузов
EDN: KTZHAS
Введение. В настоящее время государство и общество нуждаются в специалистах с высоким уровнем профессиональной подготовки, вследствие чего от преподавателей вузов требуется разработка и применение методов обучения, обеспечивающих формирование профессиональной компетентности будущих инженеров. Увеличение количества часов, отведенных на самостоятельную работу, приводит к необходимости тщательного планирования такой работы и требует активизации учебнопознавательной деятельности студента, что доказывает актуальность разработки методов, форм и способов такой активизации.
История вопроса. Вопросы познавательной активности и организации учебно-познавательной деятельности студентов освещены во множестве работ российских педагогов, методистов и психологов. Так, например, в своей работе Г.А. Петрова и Е.В. Гульбинская [Петрова Г. А., с. 97] предлагают использование информационных технологий для формирования ключевых компетенций. В сфере инноваций ими внедряется деятельностный подход в виде модульного обучения, содержащий эле- менты управления учебно-познавательной деятельностью студента. Г.А. Каменева и Т.А. Бондаренко [Каменева Г.А., с. 172] анализируют понятия познавательной активности (ПА) и учебнопознавательной деятельности студентов (УПДС); показываются условия активизации такой деятельности; выделяют уровни развития ПА, вводят критерии их оценивания, подчеркивают необходимость включения информационных технологий в образовательный процесс. Л.В. Климбей, Н.В. Ядрова и Р.М. Нуржанова в своей работе [Климбей Л.В., с. 206] показывают, что деятельностный характер обучения реализуется на принципах активного обучения, рассматривают ПА в контексте коммуникативного, исследовательского подхода, что способствует переходу на новый уровень взаимодействия с обучающимися. Проблемы активизации учебно-познавательной деятельности студентов при изучении ими математики рассматриваются, в частности, в работах Т.Л. Анисовой, Р.Н. Афониной, Г.С. Жуковой [Анисова Т.Л., с. 2; Афонина, Р. Н., с. 94; Жукова, Г. С., с. 252]. Так, Т.Л. Анисова разрабатывает многоуровневую систему математических задач, выступающую не только средством обучения, но и инструментом оценки математической компетентности. Г.С. Жукова описывает методику и средства развития творческого мышления, способствующего формированию современного специалиста, описывая одно из креативных занятий на тему «Дифференциальные уравнения», активизирующее познавательную активность студентов при изучении математики. В.П. Кузнецов и Е.Н. Рябино-ва [Кузнецов В.П., с. 14] разрабатывают персонифицированную технологию обучения математике, формирующую системное, последовательное и критическое мышление. Она основана на матричной модели УПДС и обладает свойством инвариантности к изучаемой проблеме или дисциплине. Авторы настоящей работы также неоднократно обращались к теме организации самообразовательной деятельности студентов технических специальностей при изучении различных разделов математики [Черницына Р.Н., с. 1092], [Гуменникова Ю.В., Черницына Р.Н., Камальдинова З.Ф., Ахмадуллин Ф. Р.].
Методы исследования. Теоретические методы исследования выбраны в соответствии с целями исследования – это анализ и систематизация научной литературы по вопросам активизации учебнопознавательной деятельности студентов, анализ методической литературы по проблемам подготовки будущих инженеров, анализ содержания дисциплины «Математика» и синтез, обобщающий результаты этого анализа. Эмпирические методы включали педагогические наблюдения и измерения, а также анализ результатов деятельности студентов.
Результаты исследования. В данной работе рассматривается один из возможных методов активизации учебно-познавательной деятельности студентов вуза, для чего УПДС предлагается разделять по уровням. При этом первым (простейшим) уровнем познания является отражение, вторым – осмысление. Третьим уровнем будем считать алгоритмирование, четвертым (наивысшим) – контролирование. На каждом из перечисленных уровней познания реализуются определенные психологические процессы. Отражение показывает, как обучающийся воспринимает изучаемый материал. Здесь используются память, ощущение, воображение, восприятие. На уровне осмысления производится обработка полученной информации и поиск способов решения с активизацией мыслительного процесса, также активно задействуется память. На уровне алгоритмирования формируется последовательность действий для решения задачи, здесь активно используется воображение, память, мышление, сознание, речь. Наконец, последний уровень – контролирования – требует исследования верности результата и его корректности. Он формирует у обучающихся навык подвергать результаты своей деятельности анализу, контролировать их. Как и на предыдущих уровнях, здесь активно задействуются разнообразные психологические процессы, в числе которых память, речь, внимание, а также активное мышление.
Из сказанного выше следует, что каждый уровень познания является сложной синергетической категории. На всех этапах познавательной деятельности (ПД) [Черницына Р.Н., Гуменникова Ю.В., Кузнецов В.П., Ахмадуллин Ф.] существует определенная иерархическая совокупность данных уровней. Процесс усвоения учебного материала обучающимися можно представить в виде матрицы [Tymoschuk N.A., с. 481]. На каждом уровне ПД происходит последовательное перемещение по этапам ПД: узнавание → воспроизведение → применение → творчество. Символом Y будем обозначать ij определенный объем усвоенного материала в каждой ячейке познавательно-деятельностной матрицы [Рябинова Е.Н., с. 192].
Остановимся более подробно на примере реализации первого, элементарного вида ПД, при решении которого на этапе узнавания происходит перемещение от отражения к контролированию, представленное в таблице 1.
Таб. 1. Структура первого этапа познавательной деятельности (The structure of the first stage of cognitive activity)
|
Уровни ПД Этап ПД |
Узнавание |
|
Отражение |
Y 1 1 |
|
Осмысление |
Y |
|
Алгоритмирование |
Y li |
|
Контролирование |
Y |
Рассмотрим математическое задание раздела «Аналитическая геометрия» первого уровня сложности, схема решения которого состоит из четырех шагов.
Задача. Записать уравнение кривой второго порядка, изображенной на рисунке 1.
Рис. 1 . Кривая второго порядка (Second-order curve)
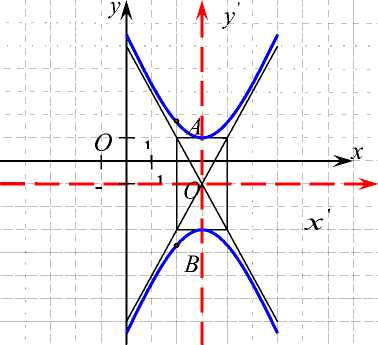
В таблице 2 представлено решение задачи в соответствии с предложенной схемой организации УПДС.
Таб. 2. Поэтапное решение задачи
(Step-by-step solution of the problem)
|
Учебные элементы |
Действия |
|
Y – отражение (этап узнавания) |
Понимание смысла задачи, определения вида кривой (гипербола), запись ее канонического уравнения: 2 2 xy +--h -— = 1, — 2 j 2 , a b определение ее действительной и мнимой полуосей. |
|
Y – осмысление (этап узнавания) |
Нахождение действительной полуоси b = 2 ; мнимой полуоси а= 1; координат центра гиперболы O (3; - 1) . |
|
Y – алгоритмиро- |
Если центр гиперболы находится в точке O ( х 0; у 0) , а - ее мнимая |
|
вание (этап узнавания) |
полуось а b - действительная, то уравнение этой кривой имеет вид: ( x - x o) 2 .( y - y o ) 2 , m 2 + ,2 — 1 . (1) a b В нашем случае x 0 — 3 , y 0 —— 1 , a — 1 - мнимая и b — 2 - действительная полуоси. Подставив найденные параметры в (1) получаем искомое уравнение: — ( x —£ + ( y ^— 1 . (2) 1 4 |
|
Y - контролирование (этап узнавания) |
Для проверки правильности полученного уравнения придадим х какое-либо произвольное значение, к примеру x — 2 , тогда (2 — 3) 2 ( y + 1) 2 + — 1 , 1 4 Откуда ( y + 1) 2 — 8 ; у + 1 — ± 2,83 ; у — 1,83 ; у 2 — — 3,83 . Получаем координаты точек A (2;1,83) и B (2; — 3,83) отмеченных на кривой, что позволяет убедиться в правильности составленного уравнения (2). |
Ответ: уравнение кривой, изображенной на рисунке, имеет вид:
( x - 3) 2 ( y + 1) 2
---1--— 1 .
-
1 4
Выводы. Рассмотренный в работе подход дает возможность объединить все учебные задания дисциплины в общую систему. Весь учебный материал распределяется по четырем уровням, соответственно степени сложности заданий. Предложенная система позволяет активизировать учебнопознавательную деятельность студентов вуза. УПДС рассматривается как четырехэтапная, (узнавание, воспроизведение, применение и творчество). На каждом этапе реализуются уровни познания: отражение, осмысление, алгоритмирование и контролирование. Учебный материал, применяющийся для изучения математики, может быть рассмотрен как относящийся к одному из таких уровней. Применение предложенной методики способствует формированию и развитию познавательной активности и активизации учебно-познавательной деятельности обучающихся.


