К вопросу об изгибе многослойной композитной пластины

Композитная пластина представляет собой совокупность однонаправленных слоев с различными углами ориентации волокон. Рассмотрим некоторый слой, отнесенный к координатам 1, 2, 3, связанным с направлением армирования. В однонаправленном материале ось 1 совместима с направлением волокон. Ось 3 ортогональна плоскости армирования. Предположим, что элемент находится в условиях плоского напряженного состояния. Поскольку оси координат 1, 2 являются осями ортотропии, закон Гука для слоя может быть записан в виде

σσ e1 =  1 - µ12

E1

σ 2 e =

σ µ 21    ¹ ,

E 1

e 12 =

τ 12

G 12

где - E\ , Е₂ и G_n - модули упругости в направлениях 1, 2 и модуль сдвига в плоскости слоя; ^ ₂, № i - коэффициенты Пуассона.

Равенства (1) могут быть разрешены относительно напряжений:

О = ^E 1⁽ e l + № 12 e 2 );

а 2 = E2( e 2 + №21 ei);       (2)

^Т 12 = G 12 e 12

где E₂ = E ₂/(1 - №₂№ i ). Здесь имеет место условие симметрии упругих постоянных E 1 № 12 = ^E 2 № 21 .

Введем ортогональные координаты а , в , Y и предположим, что ось 1 армированного слоя составляет с осью α угол ϕ . Статические соотношения, связывающие напряжения в системах координат а , в и 1, 2, следующие:

аа = а Cos2^ + а2Sin2^ - тSin12^;

Ор = а Sin2^+а Cos2^+т Sinn 2^;   (3)

т_ар = ( а — а ₂) Sin ^ Cos ^ + т ₂Cos 2 ^ , а геометрические соотношения, позволяющие выразить деформации в системе координат 1, 2 через деформации в осях а , в , можно записать следующим образом:

e = e Cos ² ϕ + e Sin ² ϕ + e Sin ϕ Cos ϕ ;

e = e Sin ² ϕ + e Cos ² ϕ - e Sin ϕ Cos ϕ ; (4) e ₁₂ = ( e _β - e _α ) Sin 2 ϕ + e _αβ Cos 2 ϕ .

Получим соотношения, связывающие напряжения а _а ,О р т _ар  с деформациями

e _a , е в , e _ae . С этой целью подставим деформации е₁, е ₂, е ₁₂ (4) в закон Гука (2), а полученные в результате этой подстановки напряжения ^ , ^ ₂ , Т₂ — в соотношения (3). После некоторых преобразований запишем физические соотношения для слоя, армированного под углом ϕ к оси α :

σα = A11eα + A12eβ + A13eαβ;

e ₁₃ = e _αγ Cos ϕ + e _βγ Sin ϕ , e ₂₃ = e _βγ Cos ϕ - e _αγ Sin ϕ .

С помощью равенств (7)–(11) можно

получить соотношения типа (5):

τ αγ = A 44 e αγ + A 45 e βγ ,

τ βγ = A 54 e αγ + A 55 e βγ ,

где

σ_β = A ₂₁ e _α + A ₂₂ e _β + A ₂₃ e _αβ ;

τ αβ = A 31 e α + A 32 e β + A 33 e αβ , где

A = E Cos ⁴ ϕ + E Sin ⁴ ϕ +

+ 2( E µ + 2 G ) Sin ² ϕ Cos ² ϕ ;

A =A =Eµ +(E +E -

A = G Cos ² ϕ + G Sin ² ϕ ;

A = G Sin ² ϕ + G Cos ² ϕ ;

A = A = Sin ϕ Cos ϕ ( G - G ).

В соответствии с гипотезами, приведенными в работе [1], закон распределения перемещений по толщине пластины можно

-

2( E µ + 2 G )) Sin ² ϕ Cos ² ϕ ;

A = ESin ⁴ ϕ + E Cos ⁴ ϕ +

+ 2( E µ + 2 G ) Sin ² ϕ Cos ² ϕ ;

A = A = Sin ϕ Cos ϕ ( E Cos ² ϕ -

- E Sin ² ϕ - ( E µ + 2 G ) Cos 2 ϕ );

A = A = Sin ϕ Cos ϕ ( E Sin ² ϕ -- E Cos ² ϕ + ( E µ + 2 G ) Cos 2 ϕ );

A = ( E + E - 2 E µ ) Sin ² ϕ Cos ² ϕ + + G Cos ² ϕ .

представить в виде

uα = u(α,β) +γθα(α,β), uβ = v(α,β) +γθβ(α,β),

где u и v – перемещения точек срединной по-

верхности пластины в направлениях α и β

соответственно, а θ α и θ β – углы поворота нормали к срединной поверхности пластины:

θα =ψα

∂ω-   , θα =ψβ

∂α

∂ω ∂β.

Закон Гука для касательных напряже-

ний τ ₁₃ , τ ₂₃ и деформаций сдвига e ₁₃ , e ₂₃

имеет вид:

τ 13 = G 13 e 13 ,

τ 23

= G 23 e 23 ,

где G и G – модули сдвига слоя.

Запишем соотношения, связывающие касательные напряжения и деформации сдвига в координатах а , в , Y и 1, 2, 3:

Здесь ω – перемещение по нормали к срединной поверхности пластины, ψ _α и ψ β – усредненные по толщине пластины деформации поперечного сдвига [1].

В соответствии с соотношениями (13), распределение деформаций по толщине пластины имеет вид:

eα = (εα +γκα), eβ = (εβ +γκβ), (15) eαβ =ζαβ + γχβa,

ταγ = τ13Cosϕ-τ23Sinϕ, τ = τ Cosϕ+τ Sinϕ;

где

∂ u        ∂ v         ∂ u   ∂ v

εα = ∂ α , εβ = ∂ β , ζαβ = ∂ β + ∂ α ;

(16) ∂ θ     ∂ θ      ∂ θ  ∂ θ

κ =   α κ =   β χ =   α +   β α  ∂ α , β  ∂ β , αβ  ∂ β  ∂ α

τ13 = ταγCosϕ+τβγSinϕ, τ23 = τβγCosϕ-ταγSinϕ;

e _αγ = e ₁₃ Cos ϕ - e ₂₃ Sin ϕ , e = e Cos ϕ + e Sin ϕ ;

Соотношения (16) представляют собой геометрические уравнения, связывающие деформации срединной поверхности с перемещениями и углами поворота нормали.

Усилия и моменты, приходящиеся на единицу длины, определяются следующим образом:

h /2	h /2
N a = f ° a d Y , N p =	f ° p d Y ,
- h /2 h /2	- h /2	(17)
N ap = f Tap d Y ;
- h /2
h /2	h /2
M a = f V a Y d Y , M p	= f V p Y d Y ,
- h /2 h /2	- h /2	(18)
M ap = f Tap Y d Y' ;
- h /2
h /2	h /2
Q a = f Ta 7 d Y , Q p =	f Tp 7 d Y ,	(19)
- h /2	- h /2

Здесь

1	_ Cos 2 m Sin 2 m
G a,/	G 13       G 23   ,         (27)
1	Sin m Cos m
—	1                                 ■
Gpr	G 13       G 23

где h - толщина многослойной пластины; N _a , N p , N ap — мембранные усилия; M _a , M p , M _a p -моменты; Q _a , Q p - поперечные усилия.

Подставив в уравнения (17)–(18) напряжения (5) и учитывая соотношения (15), получим:

^N a = B 11 ^£a + B 12 ^£p + ^C 11 ^Ka + ^C 12 ^Kp ,

Np = B21Sa + B22Sp + C21Ka + C22Kp ,

N ap = B 33 ^ ap + ^C 33 ^X ap ;

^M a = ^C 11 ^£a + ^C 12 ^£p + ^D 11 ^Ka + D 12 ^K p ,

Mв = C21£a + C22£P + D21K + DК ,

^M ap = ^C 33 ^Zap + D 33 X ap ■

Здесь h/2

mn      I mn 1 ;V /

• -    h /2

h /2

Cmn = f A„„ldr,(23)

• -    h /2

h /2

Dmn = f AmnY2dY ■(24)

• -    h /2

Эти выражения определяют мембранные B mn , смешанные C _mn и изгибные D _mn жесткости многослойной пластины.

Для поперечных усилий, в соответствии с гипотезами [1], получим:

^Q a = ^K a W a , ^Q p = ^K p W p ,     ⁽²⁵⁾

Соотношения (20), (21) и (25) – физические уравнения для многослойной пластины, связывающие усилия и моменты с деформациями. Отметим, что формулы (20), (21) и (25) получены в предположении, что пластина армирована парными спиральными слоями (под углами ±q>).

Уравнения равновесия многослойных пластин для случая действия нормального давления q имеют вид

N    .    '    — 0,    '•    +	dNaB —ap = 0;
da   dp     dp Q + ^ — q 5a   dp M    M  - Q. — 0, da    da dмв  dмав —- + —— - QB = 0. dp   da	da	(28)

Подставив в уравнения (28) выражения для усилий и моментов (20), (21) и (25) с учетом геометрических соотношений (16), получим разрешающую систему уравнений для многослойной композитной пластины:

^B 11

d 2 u da 2

⁺ B 33

d 2 u dp2

+

+ (B 33 + B12)

+ Cii(

^{d 2} V a da ^г

d² v dadp

—

d ³ ю da³

+

)+

где
K a	= h 2	h /2 f dL J G Gh /2 ^a7 J	-
K p	= h 2	h /2 f dr. <- h /2 ^pr J	-

d 2W n    d3 о

+ c12(     --d#-) + dadp  dp2da

+ C33(

^d ^ a dp ²

^d 2 ^ p dadp

2    J = 0

dadp ²

B22

d 2 v

др2

+ B33

d2 v

да2

+

(B 33 + B12)

d2 u

∂α∂β

+

+ C 22 (

d 2Vp

d 3p

др2

-

др3

)+

+ C 21(-

д V

d 3p

-

дадв  да2 др

)+

+ C 33 (

^д 2 V p

да2

+

^{д 2} У а

-

-

д Р

дрда2

K α

∂ψα

∂α

∂α∂β

) = 0,

+K y

∂ψβ

∂β

= q,

C 11

д 2 u

да2

+ с

⁺ ^33

д 2 u

др2

+

( C33 + C12)

д 2 v

∂α∂β

+

+ D ii (

^{д 2} У а

д 3р

да2

-

да 3

■) +

+ D 12 ⁽

^д 2 V p

д 3р

-

дадр  др2 да

■) +

+ D 33 ⁽

^{д 2} У р

да2

+

д V

-

-

д 3р

дрда2

∂α∂β

) = 0,

С

д 2 v

др2

+ с

⁺ ^33

д 2 v

да2

+

+ (C33 + C12)

д 2 и

∂α∂β

+

+ D 22 ⁽

^^ в

д 3р

др2

-

др3

■) +

+ D12(

д V

д Р

-

дадв  да2 др

■) +

+ D 33 (

д V

др2

+

^{д 2} V p

-

-

д Р

дадр2

∂α∂β

) = 0.

Система (29)–(33) соответствует общей расчетной модели многослойной пластины и учитывает как возможную несимметричность в расположении слоев, так и деформации поперечного сдвига.

Построение аналитического решения системы (29)–(33) возможно только в некоторых частных случаях. Приведем решение за-(30) дачи для шарнирно опертой прямоугольной пластинки шириной а и высотой b , находящейся под действием нормального давления q . Граничные условия будут удовлетворены, искомые функции представить в виде двойных тригонометрических рядов:

∞∞ р = V V wm„SinAmаSin-A„P, mn      m         n~ , m=1 n =1

∞∞ u = EE UmnC0SЛmаSinЛnP, m =1 n=1

∞∞ v = EE VmnSinЛmаC0SЛnP,   (34)

m = 1 n = 1

∞∞

ψα=∑∑^mnCosAmаSinAnP, m =1 n=1

∞∞

Vp =EEVmnSinЛmаC0sЛnP, m =1 n =1

(32) где        A _m = пт / a , A n = nn / b .

Для определения неизвестных коэффициентов разложим функцию нагрузки q ( а , в ) в аналогичный двойной ряд Фурье:

∞∞ q (а, P) = EE fm^SinAmOSininP,  (35)

m = 1 n = 1

где

f mn

ab

— f f f ( а , P ) Sin A_mа Sin A_nP d а d p . ^ab 00

Подставив выражения (34) в систему разрешающих уравнений (29)–(33), из сравнения коэффициентов при одинаковых тригонометрических функциях в левых и правых частях уравнений системы получим:

B^A2 и ^B^u +

11 m mn     33 nn mn

(B^+B.PAAv +

33     12 n m mn

+    C11(AmVmn - AmPmn ) ++    C12(AnAmVmn - ^Pm^mn ) + +    C33(An^mn + AnAmVmn -

² n m mn      ,

^B 22 ^{λ 2} n^vmn ^{+ B} 33 ^{λ 2} m^vmn ⁺

+ ( B 33 + B 12 ) λ n λ m u mn +

+ C ₂₂( λ ² _n ϕ _mn - λ ³ _n ω _mn ) +

+ C ₁₂ ( λ _n λ _m ϕ _mn - λ ² _m λ _n ω _mn ) +

+ C33(λ2mψmn + λnλmϕmn -

- 2 λ ² m λ n ω mn ) = 0,

K α λ m ϕ mn + K β λ n ψ mn = f mn ,

C 11 λ m u mn + C 33 λ n u mn +

+(C +C )λλv +

33     12 n m mn

+ D ₁₁ ( λ ² _m ϕ _mn - λ ³ _m ω _mn ) +

+ D ₁₂ ( λ _n λ _m ψ _mn - λ ² _n λ _m ω _mn ) +

+ D33(λ2nϕmn + λnλmψmn - - 2λ2nλmωmn) + Kαϕmn = 0,

C 22 λ n v mn + C 33 λ m v mn + + ( C 33 + C 12 ) λ n λ m u mn + + D ₂₂( λ ² _n ϕ _mn - λ ³ _n ω _mn ) + + D ₁₂ ( λ _n λ _m ϕ _mn - λ ² _m λ _n ω _mn ) + + D ₃₃ ( λ ² _m ψ _mn + λ _n λ _m ϕ _mn -- 2 λ ² _m λ _n ω _mn ) + K _βψ _mn = 0.

Решение полученной системы линейных алгебраических уравнений можно построить, например, при помощи прикладного пакета Mathematica. Исследуем, как влияет учет деформаций поперечного сдвига на значение прогиба в зависимости от толщины пластинки (компоновка 45/-45/-45/45). Геометрические характеристики пластины: a = b = 1м . Упругие характеристики материала пластины: E = 140 ГПа ; E = 7 ГПа ; µ = 0,24 ; G = 27,5 ГПа .

В табл. 1 приведены значения прогибов в центре углепластиковой пластины, находящейся под действием равномерно распределенной нагрузки.

Таблица 1. Зависимость величины прогиба, рассчитанной по общей теории и по теории, не учитывающей деформации поперечного сдвига, от толщины пластины

Толщина пластинки, м	Общая теория, м	Без учета сдвиговых деформаций, м
0,001	6,59⋅10-4	6,59⋅10-4
0,004	6,59⋅10-5	6,59⋅10-5
0,016	1,62⋅10-7	1,60⋅10-7
0,064	2,93⋅10-9	2,51⋅10-9

Как видно из табл. 1, учет сдвиговых деформаций необходим только для относительно толстых пластин ( h/a ≥ 0.064 ); в случае тонких пластин ( h/a ≤ 0.016 ) влиянием деформаций поперечного сдвига можно пренебречь.

Построение аналитических решений для многослойных пластин возможно только для некоторых частных случаев. В общем случае для расчетов целесообразно использование различных специализированных программных комплексов. Одним из наиболее популярных комплексов является пакет ANSYS. Теоретической основой его служит метод конечных элементов.

В конечно-элементной форме основное разрешающее уравнение может быть записано следующим образом:

[K] {u} = {F}, где [K] – матрица жесткости системы; {u} – вектор узловых перемещений;{F} – вектор узловых нагрузок. В табл. 2 приведены результаты вычисления прогибов в центре шарнирно закрепленной пластины, полученные аналитически и при помощи пакета ANSYS.

Таблица 2. Сравнение результатов точного решения и решения с помощью пакета ANSYS

Компоновка	ANSYS, м	Аналитическое решение, м
0/90/90/0	0,86⋅10-3	0,86⋅10-3
45/-45/-45/45	0,66⋅10-3	0,66⋅10-3

Полученные результаты показывают, что пакет ANSYS обеспечивает высокую точность вычислений.

Примечательной особенностью пакета ANSYS является возможность проведения общего динамического анализа. Основное разрешающее уравнение динамики в конечноэлементной форме (без учета эффектов демпфирования) можно представить следующим образом:

[M] { u } + [K] {u} = {F(t)}, где [М] - матрица масс системы; { U } - вектор ускорений. Для нахождения неизвестных используется схема прямого интегрирования по времени, базирующаяся на методе Ньюмарка.

В качестве примера исследуем поведение пластинки, находящейся под действием распределенной поперечной нагрузки. Закон изменения нагрузки с течением времени представлен на рис. 1.

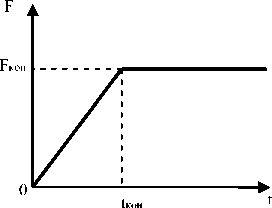
Рис. 1. Закон приложения нагрузки

Результаты расчетов представлены на рис. 2.

Значение

₀ п _, р ₀ ог ₀ иб ₂ а ₀ (м ₀ )

0,00150

0,00100

0,00050

0,00000

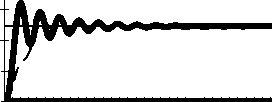
°л\ ^А'ь'. й\ Й Й Й Й Й Й Й Й ъ' 0'0- о- о- \- \- \- \- \- v w v v

Время (с)

^^^^^^М tкон = 0.2 с                     tко стационарное решение

Рис. 2. Значение максимального прогиба пластины в зависимости от скорости нагружения

Как видно из графика, поведение конструкции на начальной стадии нагружения (до выхода на стационарный режим) существенно зависит от скорости приложения нагрузки.