К вопросу структурной надежности в мобильных сетях в условиях разрушающих информационных воздействий

Хорошо известно, что структурная надежность сетей связи связана прежде всего с заданными критериями живучести и соответствующими структурными и временными показателями этих сетей [1]. Во-вторых, те и другие (критерии и показатели) существенно зависят от типа сетей связи и их назначения. Отсюда следует, что само понятие живучесть и ее составляющая часть, структурная надежность для каждого типа сети связи, должно определяться согласно виду и назначению данной сети. Кроме того, классификация атак на сеть [2], также накладывает свой отпечаток на задачи анализа структурной надежности сетей связи. В данной статье рассматриваются две задачи анализа структурной надежности мобильных сетей передачи данных в которых анализируется состояние двух мобильных корреспондирующих пар x и y при условии вывода из строя базовых станций сети радиосвязи.

1.    Постановка задачи

Предположим, что базовая сеть мобильной связи представляет собой граф G(X,R), в котором вершинам соответствуют базовые станции сети, а ребрам линии связи. Пусть, также существует пара абонентов, которые потенциально могут быть связанными с любой базовой станцией по соответствующему радио-каналу. Другими словами сеть мобильной связи можно представить в виде нестационарной гиперсети [3] в которой первичная сеть состоит из графа базовой сети и гиперребер добавляемых ко всем вершинам графа. Вершине z инцидентно n(z) различных гиперребер, если и только если, соответствующая базовая станция может работать на n(z) радио-каналах. Таким образом, первичная сеть гиперсети задается гиперграфом. Здесь мы будем предполагать, что станции работающие с нашими абонентами не «мешают» друг другу. Очевидно, что вершины x и y будут инцидентны всем добавляемым гиперребрам. Таким образом, абонент потенциально может работать с любой станцией и по любому каналу. Если, это не так, то в модели легко предусмотреть любую конфигурацию. Очевидно, что вторичная сеть гиперсети задается мультиграфом в котором из каждой вершин x и y выходит n(z) ребер в вершину z проходящих по соответствующим гиперребрам гиперсети. На рис. 1 приведен пример такой гиперсети.

Здесь нестационарность определяется уже тем, что абоненты вторичной сети передвигаясь по местности переходят в зону действия очередных базовых станций. Поэтому, зная маршрут абонента можно легко составить расписание работы линий связи вторичной сети. Кроме того, задержки в каналах и станциях первичной сети показывают временную зависимость прохождения информации по мобильной сети.

Проблема усложняется еще тем, что базовые станции могут быть выведены из строя различными способами. Например: физическое уничтожение, включение широкополосной помехи, вывод некоторых каналов из строя узкополосной радио-помехой. Кроме того, современные сети мобильной связи могут быть атакованы разрушающими информационными воздействиями (РИВ). С точки зрения физического уничтожения можно предположить, что противнику известна структура сети и поэтому он будет пытаться нанести удар по узкому месту, т.е. нанести мобильной сети связи максимальный урон при минимальных затратах. Следовательно, мы можем рассмотреть возможные варианты воздействия на сеть и при этом вычислять такие важные показатели, как пропускная способность, так и время задержки пакетов или сообщений в сети. Рассмотрим математическую модель такой сети и соответствующие задачи вычисления существенных параметров сети.

2.    Основные определения

Определение: Нестационарная гиперсеть S(t)=(X, V, R) включает следующие объекты [3]:

X = (x 1 ,...,x n ) - множество вершин;

• V = (v 1 ,.,v g ) - множество ветвей;

• R = (r 1 ,.,r_m1) - множество ребер;

Vxi eX сопоставлена в> емкость вершины (буфер) и

• 1,    если вершина i работает в момент t

  Y i⁽ t ) = *

  
  

• 0, иначе

Vv j eV сопоставлена a j (t)>0 функция пропускной способности ветви;

Vrk eR сопоставлена Sk(t)>0 функция пропускной способности реб ра.

Определение: [3] Поток по ребру rk(из xi в xj) есть функция fk : [0, T] ^ R+

со следующими ограничениями:

V t >  ⁰, V r k G ^R f_k ⁽ t ) <  ^{5 (} t )   и ^V V j G V £   f k ⁽ t ) <  ^a j ⁽ t )

r k ^G F ^{- l}( v j )                       (1)

Пусть поток идет из вершины x1 в xn, тогда на поток налагается ус- ловие:

V t >  0 V x i g X \{ Х | , x , }   X f k ( ‘ ) - Z f, ( t ) <  в

V r k = (..., i )                V r , = ( i ,...)

3. Задача поиска максимального (s-t) потока в нестационарной гиперсети

В данном разделе будут показаны две модели сведения нестационарной гиперсети к гиперсети, позволяющие решать различные задачи теории нестационарных гиперсетей.

В частности, такой задачей является поиск максимального потока, который в свою очередь является интегральным показателем структурной надежности мобильных сетей электросвязи.

Постановка задачи: Найти максимальный поток из вершины x i в xn

Ф = ^max X f ⁽ r k )

^V r k = (..., ^x n )

в нестационарной гиперсети S(t) за интервал времени [0,T] .

Упрощение: Разобьем интервал времени на m частей. В каждый отрезок времени [t_p, t_p+1] будем считать, что гиперсеть S(t) в каждом таком интервале является стационарной с параметрами:

V v j g V a j : = J a j (t ) dt ;   V r k g R 5 _k : = J 5 _k ( t ) dt .

t p t p

Модель 4.1:

В каждый момент времени поток есть сумма трех потоков:

1)Максимальный поток из вершины x 1 в x n ,

2)Максимальный поток из всех вершин (кроме x ) в xn (открытие буферов);

3)Максимальный поток из x 1 во все вершины (кроме xn) (заполнение буферов).

Очевидно, описанный выше поток меньше или равен максимального (x -x n )потока в гиперсети S(t) .

Модель 4.2:

Определим гиперсеть G=(Y,U, P) с множеством вершин YXxT, (x i , t k )eY (рис.1)

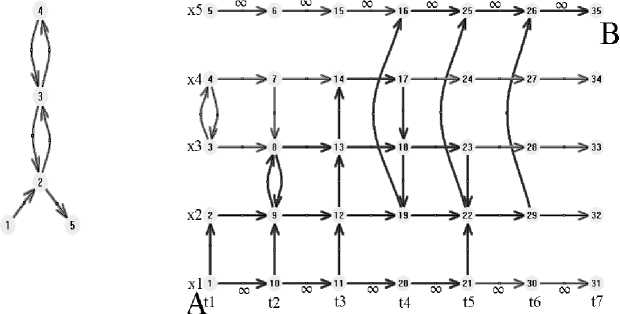
Рис 1. на рисунке показаны только вершины и ребра гиперсетей S ( t ) и G соответственно

Из вершины (x i , t_k) в (x j t l ) идет ветвь u_ceU тогда и только тогда, когда:

• а)    i=j и l=k+1;

• b)    i ^ j и k=l.

Для дуг типа a) определим вес tk + tk+1 2

d _c

• t k + t k + 1 ^

• ²    ^ , если i=1

или i=n,то d c x.

Для остальных ветвей веса задаются выражением:

d c = ⁽ t k + 1

—

t k X

f t k + t k + 1 Y

( 2 )Y

f t k ⁺ t k + i y

( 2 )Y

^f t k ⁺ t k + 1

I 2

Множество ребер P задается аналогично ветвям, только вместо функции a = (t) участвует 5 = (t).

Утверждение:

Если функции a(t), P(t), 3(t) кусочно-постоянные, то поток (x 1 -x n ) в гиперсети S за интервал времени T=(t 1 ,...,t m ) равен потоку в гиперсети G из вершины (x 1 , t 1 ) в (x n , t m ) [3].

4.    Задача поиска кратчайших по задержке простых v-цепей в нестационарной гиперсети

Определим функции задержки:

Vr k eR сопоставлена T_k(t)>0 задержка в ребра (зависит от задержки в каждой внутренней вершине ребра, плюс задержка в каждой ветви через которое проходит ребро).

Определение: Маршрут (x₀,r 1 ,x 1 , ^,r_k,x k ) в гиперсети S называется v-цепью , если каждая ветвь используется не более одного раза [3].

Постановка задачи: Для заданной пары вершин x и у, найти кратчайшую по задержке v-цепь в нестационарной гиперсети G .

Модель 5.1:

В случае, если задержки целочисленные, построим гиперсеть G (Y, U, P) со множеством вершин YXxT, (x i , t k ) eY . Множество ребер P строится по схеме из [4]. Множество ветвей U состоит из множества V , через каждую ветвь которого проходят не только соответствующие ребра из R , но и их копии во все моменты времени. Для ребер, соответствующих ожиданию в вершине, сопоставлены идентичные им ветви из U . Данное сведение объектов позволяет решать практически все задачи на гиперсетях связанных с потоковыми и метрическими характеристиками, которые в свою очередь зависят от времени.

Утверждение: Кратчайшая по задержке v-цепь из х 1 в x n в нестационарной гиперсети S(t) совпадает с кратчайшей v-цепью в гиперсети G из (x 1 ,t₀) в слой x n .

Модель 5.2:

Пусть задержки в гиперсети нецелочисленные. Для простоты будем считать, что в задаче поиска v-цепей накладывается еще одно условие: запрет на прохождение цепи одной вершины более одного раза, т.е. требуется найти простую цепь [3], кратчайшую по задержке.

Построим гиперсеть G=(Y,U,P) .

Множества ребер P и вершин Y представляют собой дерево: вершина у 1 соответствует х 1 ; количество потомков у корня у 1 равно количеству исходящих дуг х 1 в момент времени t=0, веса дуг исходящих из у 1 равны т_к(0) для соответствующих к . Пусть в S(0) вершина х 1 соединена с вершиной х₂ ребром r 1 с задержкой т 1 (0) , а момент времени т 1 (0) вершина х₂ с х₃ ребром r₂ .Тогда из вершины дерева у₂ исходит дуга весом т₂(т 1 (0)) , и т.д. Дерево строится с учетом, чтобы по любой цепочке из корня в соответствующем S не было повторяющихся вершин. На рисунке 2 показан пример построения дерева G. Безусловно, такое построение трудоемко и для ограничений дерева можно применить метод ветвей и границ, который не будет образовывать потомков, если суммарная задержка уже превосходит некоторую величину.

Что касается построения множества ветвей U, то оно аналогично построению в предыдущей модели.

Утверждение: Кратчайшая простая цепь (по величине задержки) в гиперсети G больше или равна задержке кратчайшей простой цепи в S(t).

Аналогичную модель можно построить и для v-цепей.

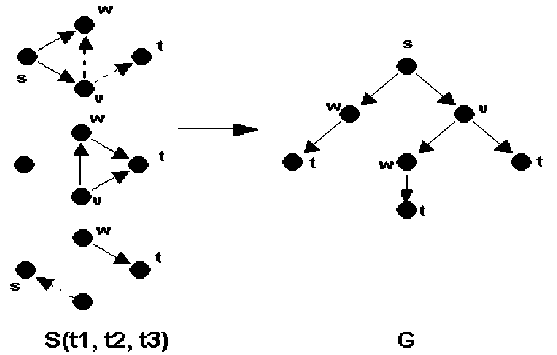
Рис. 2. Построение дерева G

Заключение

Для ряда задач на нестационарных гиперсетях применимы методы сведения их к стационарным, что позволяет получить решения. Причем эти решения отражают временную динамику изменения пропускных способностей, задержек (т.е. свойства, присущие реальным информационным сетям).

Таким образом, очевидно, что с помощью нестационарных гиперсетей можно исследовать различные структурные характеристики мобильных сетей передачи данных. Очевидно, что с помощью предло- женных моделей можно не только анализировать показатели сети, но всевозможные варианты атак на сеть мобильной связи. В самом деле, функции параметров элементов гиперсети могут быть любыми (с одним лишь условием, эти функции должны быть кусочнопостоянными). Но тогда, модели разрушений могут вполне моделироваться этими функциями.