К выводу эмпирических зависимостей в сейсмологии с помощью механической модели

Для количественной оценки масштаба землетрясений используется параметр, называемый магнитудой [1]. Существующие в сейсмологии эмпирические законы, позволяют через этот промежуточный параметр выразить размер очаговой зоны, освободившуюся при землетрясении энергию, время землетрясения и т.д. [1-3].

Например, одно из соотношений, устанавливающее связь между энергией Е землетрясения и магнитудой М имеет вид lgE=11,8 + 1,5М.                              (1)

Если в формуле (1) М увеличивается на 1,0, то Е умножается на коэффициент 101,5. Другими словами, сейсмическая энергия землетрясения с магнитудой М=6 примерно в 32 раза больше, чем у землетрясения с М=5 и в 1000 раз больше, чем у землетрясения с М=4 [1].

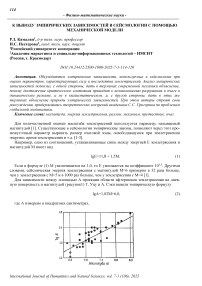
Для зависимости между площадью А проекции области афтершоков землетрясения на дневную поверхность и магнитудой (рисунок1) Т. Уцу и А. Сэки вывели эмпирическую формулу lgA=1,02M+6,0,                             (2)

где А измерено в квадратных сантиметрах.

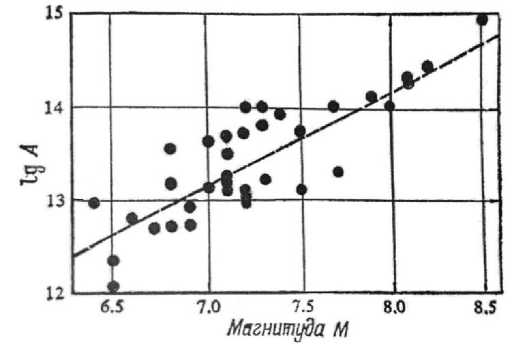
Рис. 1. Зависимость логарифма площади области афтершоков А (см2) от магнитуды М главного толчка [1]

Механизм возникновения афтершоков детально не выяснен, но, несомненно, что он связан с основным разрушением в источнике.

Аналогичную зависимость площади A' области остаточных изменений в рельефе дневной поверхности от M предложил Цубои [1]

lg A' =1,02M+5,9.

Из (2) и (3) следует, что A≈ A'

Оцука, используя данные работы Инда (рис. 2) [1], вывел формулу для верхнего предела Lm длины разлома lgLm=3,2+0,5M,

где L m измерено в сантиметрах.

Рис. 2. Зависимость магнитуды от длины разлома в модели Оцука [1]

Воспользовавшись соотношением (1), получим

Е≈L³ m

Из (5) следует правильность гипотезы объемного источника, то есть, что сейсмическая энергия пропорциональна кубу линейного размера источника.

Для характерного периода Т сейсмических волн К. Касахара установил соотношение (M>5)

lgT=0,51M – 2,59.

Для M <3 Т. Терасима предложил зависимость [1]

lgT=0,47M–1,79.

Так как имеет место (5), то между сейсмической энергией и объемом очага землетрясения соблюдается соотношение [1]

Е= в * V.                                        (8)

Формула (8) известна теперь как формула Садовского–Цубои [1-4].

В (8) параметр в * не зависит от интенсивности (магнитуды) землетрясения и даже от региона и оценивается величиной порядка 10³ эрг/ см³ [1].

Для времени T *подготовки землетрясения данной интенсивности в данном регионе (время между двумя последовательными землетрясениями данной интенсивности) М.А. Садовским с коллегами установлена эмпирическая формула [4]

lg T *=1/3lgE-3,5.                               (9)

В (9) T * измеряется в годах, Е в Джоулях.

Анализ эмпирических данных из [3] позволил им же получить соотношение lg∆T=1/3lgE–4,5,                           (10)

где ∆T – продолжительность времени проявления предвестников.

Из (9) и (10) следует дт=о,1Т*.

Аналогичные эмпирические зависимости вида

Lg дт= а *т+ Ь *, а * и Ь * - const,                  (11)

предложенные разными авторами, приведены в [1].

При сильных землетрясениях на дневной поверхности возникают значительные необратимые деформации, в частности, относительное смещение берегов разлома.

Характерная и максимальная величины U и U m смещения связаны с М соотношениями вида

Lg U=cM+d, lgU m =c m M+d m ,                   (12)

• c, d, c m , d m = const,

0,55≤ c≤0,96,     –6,69≤d≤–3,7

0,57≤ c m ≤0,67,     –4,33≤d m ≤–3,19.

Для суммарной сейсмической энергии S К. Цубои установил эмпирическое соотношение [1]

S=(2,24t+1,91) 1023.                          (13)

В (13) t измеряется в годах, S в эргах.

Одной из важнейших эмпирических сейсмологических закономерностей является закон повторяемости Гутенберга-Рихтера [5]. Они предложили связать магнитуду и среднегодовое число ударов соотношением lgN=a+b(8–M), a≈–0,48, b≈0,9,                  (14)

где N – число событий для указанного фиксированного периода времени и в заданном географическом районе, относящихся к интервалу магнитуд

(M-AM; M+AM).

Все соотношения (1) - (14) являются чисто эмпирическими и, согласно [6], не получили должного рационального истолкования, которое базировалось бы на ясных представлениях о механизме подготовки и возникновения отдельного землетрясения и о возможном взаимодействии таких отдельных процессов подготовки и возникновения землетрясений разной энергии друг с другом в данном сейсмоактивном регионе. Исключение составляют представление о постоянстве параметра 6* в (8), фиксирующее постоянство средней по объему очага плотности энергии, переходящей при землетрясении в сейсмические волны, и интерпретация соотношения (9), по ко- торому время

T *

определяется из условия,

что приток энергии извне через поверхность объема V очага будущего землетрясения при постоянстве скорости этого притока в единицу времени через единицу площади поверхности обеспечил за время T*, достижение в объ еме V предельной энергии E=6* V, приводящей к землетрясению [1-4].

С другой стороны, в механике землетрясений [1,2] с достаточной определенностью установлено, что землетрясение связано с достижением критического напряженно-деформированного состояния породы в очаге и последующего возникновения и распространения по некоторой «поверхности» (по разлому) процесса быстрого взаимного перемещения контактирующих по этой поверхности массивов породы, следствием чего является частичное снятие напряжений и генерирование сейсмических волн.

Естественно, возникает задача, с одной стороны, дать в терминах современной механики объяснение, почему достижение критического состояния приводит к возникновению разрушения в очаге в динамическом режиме, а не в квазистатическом и, с другой стороны, дать в этих же терминах объяснение природы, приведенных выше эмпирических зависимостей.

Важность такого подхода продиктована тем, что землетрясение имеет непосредственное отношение к человеческим нуждам [7, 8]. Дело в том, что для построения реального прогноза, как отмечено в [6], необходима надежная расчетная модель. До настоящего времени сейсмология представляет собой относительно простую полуэмпирическую науку [9]. Основной ее метод - накопление данных наблюдений и измерений, относящихся к сейсмическим событиям, их обработка и превращение в рассмотренные выше эмпирические формулы (например, рисунок 1,2 и соответствующие им формулы (2) и (4)). Однако при этом не прекращаются попытки построения математической теории с дальнейшим ее развитием с целью расчета процессов распространения упругих волн в земной коре при заданной схеме источника и механических свойств горных пород на трассе распространения сейсмических волн [10-11]. В дополнение к этому инструментальная сейсмология пытается реконструировать геосферы, строение Земли по глубине и изучать глубинные процессы.

Из анализа современного состояния уровня развития наук о Земле следует, что землетрясение - чисто механический процесс. Принимая самую простую модель взаимодействия литосферных плит [6, 12], можно предположить, что очагом землетрясения является место зацепления двух плит, побуждаемых к активному движению мантийными течениями. Такое зацепление временно затормаживает движение вокруг себя, но вдали движение продолжается. Поэтому в окрестности зоны зацепления накапливаются механические напряжения и, когда их значения достигают предела прочности на разрушение материала стыка плит, происходит разрушение плит по линии зацепления. Разрушение при этом происходит в динамическом режиме и энергия статических напряжений, накопленная в горном массиве вокруг зоны зацепления, освобождается и переходит в энергию генерируемых этой зоной упругих волн - возникает землетрясение [6, 12].

Такова простейшая механическая модель процесса подготовки и возникновения землетрясения, которая основана, в частности, на использовании представлений современной механики разрушения [13]. Согласно этим представлениям, разрушение может происхо- дить как в медленном режиме квазистатиче-ским образом, так и путем возникновения и быстрого распространения фронта разрушения в зависимости от того, с каким из двух основных типов задач этой теории имеем дело. Первый тип соответствует случаю, когда для увеличения размера трещины в упругой конструкции с повреждением (трещиной) приложенную внешнюю нагрузку нужно увеличивать, то есть, когда связь между разрушающей нагрузкой и размером трещины монотонно растущая. Второй тип задачи, когда этой связи соответствует «падающая диаграмма», то есть, когда большей длине разрушенной зоны соответствует меньшая внешняя нагрузка. Существуют также и «смешанные» случаи, когда при небольших размерах повреждения этот размер растет с ростом нагрузки, а затем, когда достигается некоторый максимум нагрузки, дальнейшему увеличению длины трещины соответствует меньшая нагрузка.

Описанные два основных типа задач и диаграмм разрушения различаются способом приложения нагрузки к конструкции с повреждением. Если нагрузка приложена к поверхности зоны повреждения, то трещина будет равновесной, устойчивой, разрушение будет происходить медленно, квазистатически, что, вообще-то, сравнимо с механизмом гидроразрыва пласта [14]. Если же к конструкции приложена распределенная «на бесконечности» нагрузка, то есть, если размеры зоны приложения нагрузки намного больше размера повреждения и приложена она вдали от повреждения, то статическое состояние трещин оказывается неустойчивым (возникает падающая диаграмма) [13]. Это означает, что, если такую конструкцию медленно нагружать, наращивая приложенную вдали распределенную нагрузку, то в некоторый момент, когда нагрузка достигнет величины, соответствующей точке на падающей диаграмме, наступит критический момент. Дальнейшее малейшее увеличение нагрузки или какое-либо иное возмущение приведет к несоответствию между размером трещины и величиной нагрузки.

Трещина будет распространяться в динамическом режиме со скоростями, близкими к скоростям распространения упругих волн, и первоначально накопленная вокруг трещины энергия будет превращаться в энергию упругих волн, излучаемых из этой области.

Характер нагружения в зоне зацепления литосферных плит относится ко второму случаю. Внешняя нагрузка здесь распределена «на бесконечности», то есть плиты движутся независимо от того, есть зацепление или его нет. Поэтому в момент, когда в зоне зацепления будет достигнуто предельное по нагрузкам состояние, начнется динамический тип разрушения зацепления с переходом накопленной вокруг него энергии статического поля напряжений в энергию излучаемых упругих волн, то есть возникнет землетрясение [6].

Рассмотренные выше эмпирические зависимости могут быть получены на основе изложенной здесь простейшей механической теории. Рассмотрим некоторые из них. Согласно [6], если характерный размер области вдоль «плоскости» разлома, где возникает концентрация тектонических напряжений, есть L, то к моменту начала разрушения область разлома, где сдвиговые напряжения достигли разрушающей величины Т * для материала зоны разлома, будет иметь площадь порядка L². Вокруг этой области в трехмерном объеме более прочной породы будет создана концентрация сдвиговых напряжений, спадающих от Т * при удалении от этой области по некоторому закону. При интегрировании по объему плотности упругой энергии статического поля этих напряжений получится величина порядка

Т2 L3 /2ц, где µ– модуль сдвига породы вне разлома.

В результате динамического разрушения слабого материала в зоне разлома сдвиговые напряжения на разломе упадут до Т **, так что величина энергии статического поля напряжений, перешедшей в энергию сейсмических волн, будет порядка

Т

E=

*

-Т **

2Ц

■ L 3 = е * v.

Соотношение (15) есть не что иное как формула Садовского-Цубои (8).

Согласно [6] механическое содержание соотношений в формулах Касахары (6) и Терасимы (7) состоит в том, что при возникновении и распространении упругих волн из некоторой начальной напряженной области с характерным размером L, характерный масштаб времени T в излучаемых волнах будет порядка T~L/C, где C–скорость упругих волн, что при постоянном С и приводит к формулам (6) и (7).

Аналогично могут быть выявлены механические содержания соотношений (11), 12, (13) и (14).

Таким образом, из теоретического анализа эмпирических соотношений можно получить достаточно точное их представление через механические параметры и раскрытие физического содержания этих коэффициентов. Отсюда следует, что теория развития термомеханических процессов в мантии Земли, тектонических взаимодействий литосферных плит [15] и механики разрушений в местах таких взаимодействий достаточно адекватна и на ней можно базировать, в частности, организацию систем мониторинга предвестниковых эффектов для предсказания землетрясений. Эта возможность базируется на том, что процесс созревания очага, подготовки к разрушению зоны зацепления литосферных плит происходит постепенно во времени и с какого-то момента начинает проявляться.