К задаче об управляемых вращениях динамически симметричного твердого тела
Автор: Стрелкова Н.А., Агибалова О.С.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (42), 2018 года.
Бесплатный доступ
Исследуется задача гашения экваториальной составляющей угловой скорости динамически симметричного твердого тела. Предполагается, что осевая составляющая угловой скорости является заданной функцией времени. Критерием оптимальности является минимизация энергетических затрат. С использованием принципа максимума Л.С. Понтрягина и метода усреднения в аналитическом виде построено приближенное решение. Определены оптимальные управления в форме синтеза, угловые скорости, минимальные энергетические затраты. Указано условие, когда решение рассматриваемой задачи не существует.
Оптимальное управление, вращение твердого тела, минимум энергетических затрат, принцип максимума понтрягина, метод усреднения
Короткий адрес: https://sciup.org/147245400
IDR: 147245400 | УДК: 62-50 | DOI: 10.17072/1993-0550-2018-3-89-94
Текст научной статьи К задаче об управляемых вращениях динамически симметричного твердого тела
-
1. Постановка задачи
Уравнения управляемого вращения динамически симметричного твердого тела относительно центра масс имеют вид [1 , 2 ]
Jp + ( J 3 - J ) qr — M 1 , p ( o ) = p 0,
-
- Jq - ( J з - J ) pr — m 2 , q ( o ) = q 0,
_ J 3 r — M 3 , r ( 0 ) — r 0.
Здесь J, J3 (J ^ J3) - главные центральные моменты инерции твердого тела, p, q, r - проекции вектора угловой скорости на главные центральные оси инерции, Mi (i — 1,2,3) – управляющие моменты: Mi| < M0. Предпо- лагается, что управляющий момент мал, т. е.
M MM M M << - J ( p 02+ q 02)+- Jr 02.
После перехода к безразмерным переменным и параметрам по формулам [1, 2]
pqr
^1 = —, ^2 — —, ^3 — —, ui —
ω0 ω0
M i M 0 ,
J3 0 0 02 0202
I — -j-, t — Ф t , ft) — у ®i + ^2 + ^3 , получаем
d ) 1 + ( I -1 ) ® 2 ® 3 — su 1, ® 1 ( 0 ) — ® 0,
-
- ®2 -(I -1)®1®3 — su2, ю2 (0)— ®0,(1)
М 0
[ Ia3 — su 3, ® 3 ( 0 ) — ® 3, s — —^ << 1.
Jω 02
Здесь точка означает дифференцирование по времени t ', однако в дальнейшем для упрощения записи штрих опускаем.
Рассматривается задача гашения экваториальной составляющей угловой скорости, в конечный момент времени t — T :
« 1 ( Т ) — Ю 2 ( Т ) — 0. (2)
Предполагается, что функция а3 ( t ) является заданной функцией времени t , а управление изменением экваториальной составляющей угловой скорости осуществляется при помощи одного фиксированного двигателя. Введем скалярное управление u :
u j — u cos a, u 2 — u sin а, | u | < u °, а — const.
Требуется найти управляющие функции u j ( t ) , u 2 ( t ) , удовлетворяющие соотношениям
(3) и доставляющие минимум функционалу
энергетических затрат
J = £
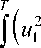
T
+ u 2 ) dt = £ j u 2 dt ,
* x I p cos w 1 u = sat l----------I,
I 2 J,
где
где время перехода T задано.
I p cos ^ satl----------
I 2
2. Построение оптимального решения
С помощью замены переменных o1 = a cos ф - b sin ф, t (5)
o 2 = a sin ф + b cos ф , ф = j ( I —1 ) ^ 3 ( t ) dT 0
первые два уравнения системы (1) и краевые условия преобразуем к следующему виду [1, 2]:
c i = u 1 cos ф + u 2 sin ф,
V .
b = - u 1 sin ф + u 2 cos ф ,
a(0) = of, b(0)= ^.(7)
a (T ) = b (T ) = 0.(8)
p cos ψ
, если
p cos ψ
< u °,
u 0signcos ψ , если
Тогда
* u 1
* u 2
p cos ψ
> u °,
w = ф - a + Y .
I p cos w 1 = cos a sat —------ ,
I 2 J,
I p cos w = sin a sat l —------
I 2
.
Подставим u 1* , u * 2 в систему уравнений
Для решения задачи (3), (4), (6)–(8) воспользуемся принципом максимума Л.С. Понтрягина [3]. Функция Гамильтона–Понтрягина имеет вид
(6) и воспользуемся методом усреднения для построения приближенного решения задач оптимального управления с фиксированным временем окончания процесса [1, 2]. Усредняя по фазе ϕ , получим уравнения
H = -£u 2 + pa£ ( u 1 cos ф + u 2 sin ф ) +
+ pb£ ( - u 1 sin ф + u 2 cos ф ) .
• £ 2П ( • / p cos w 1 , a =— j cos(ф - a)satl-------I dф,
2п О ^ 2 J
/ £ 2П I /pcoswV b =--sin(ф - a )sat l —------I аф.
2n 0 'I 2 J
Так как функция H не зависит от a и b , то из сопряженной системы дифференциальных уравнений следует, что pa , pb = const.
Преобразуем функцию Гамильтона– Понтрягина (9):
H = -£u 2 + £u p cos ( ф - a + y ) =
Используя замену переменных (14) и учитывая периодичность подынтегральных функций, найдем
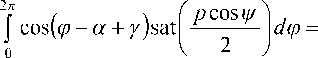
= £
-
u
-
p cos ( ф - a + y )
+
p 2 cos2 ( ф - a + y )
+ 4
π
ψ 1 2
= 4 j u0 cosw dw + 2 j p cos2 w dw =
0 ψ 1 (17)
= 2 u 0 sin w 1 + p
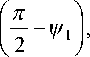
где cos Y =—, sin Y = pb, p = Vp2 + p2. (11) pp
Введем в рассмотрение функцию насыщения sat { } [4]. Из условия максимума функции Гамильтона–Понтрягина (10) и соотношения (3) получим оптимальное управление
2π j sin(ф - a
\ I p cos w 1 .
+ Y ) sat l —-— I dф =0.
Здесь ψ 1 удовлетворяет равенству
p cos ψ 1 0
---------= u .
Введем обозначение
„ 0 I n 1 ,
2 u sin w 1 + p ly- w 1 I = A
и вычислим, используя соотношения (17), (19), интегралы правых частей системы (16). Тогда уравнения для усредненных фазовых переменных примут вид
u
|
u0 cosw |
cos ψ |
||
|
, cos ^ 1 |
если |
cos ψ 1 |
|
< 1, u0 sign cosψ, если
cos ψ
> 1.
A a - s — cos y, 2π
A b - s—sin y.
2 π
cos ψ 1
Вычислим cos ψ . Из соотношений (22), (23)
следует, что
Найдем решение данной системы дифференциальных уравнений, учитывая начальные условия (7)
cos y -
—
a
=, sin y - — ' + b2
b
+ b 2
.
A 0 a - s —cos Yt + a 1, 2 π
A b - s—sin Yt + a2.
2 π
Из граничных условий (8) следует, что
A - П® °,(21)
εT
ω 0 ω 0
cosY -0, sinY -0,(22)
ω0
0 02
где a - ^0{ + a 2 .
Воспользуемся равенствами (21), (22) и пре-
образуем выражения (20):
о (, t a - ai 11- t I, b - a0 f1 - — У
2 1 T I
Из соотношений (18), (19), (21) получаем, что для определения неизвестной постоянной
ψ 1 следует найти корень трансцендентного
уравнения
1 f n sm w 1 +------1-- W1
cos y 1 k 2
πω 0 εTu 0.
Используя выражения (5), (23), найдем угловые скорости a1 (t) и a2 (t)
ω 1
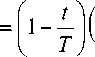
ω 10 cos ϕ
- a 0 sin ф
ω 2
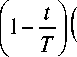
a 0 sin ф + a 0 cos ф ) ,
Тогда, применяя равенства (14) и (5), получаем
cos у - cos ( Ф — a + y ) - a cos a + b sin a
— cos ф
— sin ф
—
—
k
—
. V a 2 + b2 )
b cos a + a sin a
k
+ b 2
I
t
Ф - j ( I - 1 ) a 3 ( t ) dT .
Воспользуемся равенством (18) и преобразуем формулы (12), (13) к виду
a1 cos a + a2 sin a a1 + a2
.
Используя соотношения (3), (26),
находим оптимальные управления форме синтеза
где
*
u
—
(27),
u 1 , u 2 в
*
u 1
*
u 2
u 0
если
- u cos a ,
- u sin a ,
a1 cos a + a 2 sin a
■Ja^ + a2
a 1 cos a + a 2 sin a
^ a1 + a 2 cos ^ 1
< 1,
— u 0 sign ( a 1 cos a + a 2 sin a ),
если
a1 cos a + a2 sin a a1 + a2 cos ^1
> 1.
Таким образом, оптимальное управление u * является кусочно-гладкой функцией, принимающей, при выполнении неравенства
a 1 cos a + a2 sin a
^a1 + a 2 cos ^ 1
симости
> 1
значения ± u0 в зави-
от знака выражения
a 1 cos a + a 2 sin a ; в противном случае - графиком функции является кривая, определяе-
* - u0 a, cos a + a2 sin a мая уравнением u —--5—. 2 ---.
cos / 1 a 121 + al
Моменты времени, при которых происходит изменение режима оптимального управления,
находятся из условия
a 1 cos a + a2 sin a
^ a 1 + a2 cos / 1
= 1,
где a ( t ) и a 2 ( t ) согласно соотношениям (25)
являются известными функциями времени.
В первом приближении минимальное значение функционала (4) вычисляется по формуле
T
J * — £ j Ци *2 dtdt , 0
Здесь Ци *2) - функция, полученная в результате подстановки в (30) управления и * из (29) и усреднения по фазе ϕ . Из соотношения (29) получаем, что
u 0
, если 2cos2 ψ 1
и
a 1 cos a + a 2 sin a
< 1,
2 cos ψ 1
u 0 , если
a 1 cos a + a 2 sin a
7 2.2 _ a1 + a2 cos^j
> 1.
Рассмотрим два предельных случая, ко-π гда i/1 ^— и 1/1 — 0.
Если / 1 ^ П (управление и * является кусочно-постоянной функцией), то из уравнения (24) следует, что время окончания процесса должно удовлетворять равенству
T — п a0
1 2 ε u 0 .
В этом случае оптимальный по энергетическим затратам режим совпадает с оптимальным по быстродействию режимом гашения экваториальной составляющей угловой скорости и синтез оптимального управления получаем в виде
и * =- и ocos a sign ( a 1 cos a + a 2sin a ) , и 2 — — и osin a sign ( a 1 cos a + a 2sin a ) .
При Т — Т 1 энергетические затраты равны 2 π
J = £и Т =—и a . При Т < Т1 рассматри ваемая задача решения не имеет.
Отметим, что задача оптимального по быстродействию управления гашением экваториальной составляющей угловой скорости рассматривалась в работах [1, 2] при произвольной зависимости осевой составляющей угловой скорости от времени, а в работе [4] – при a 3 = const.
Если / 1 — 0, то из уравнения (24) получаем, что время окончания процесса равно
При T = Т 2 формуле
2 ω 0
2 £ и °'
управление и вычисляется по
и — — и
о a 1 cos a + a2 sin a
a 1 + a 2
.
Найдем оптимальное управление при T > T2, используя условие максимума функции Гамильтона–Понтрягина (10),
* p cos / и —
.
Вычислим и * , и 2 по формулам (28), (36), подставим полученные выражения в систему уравнений (6) и произведем усреднение по фазе ϕ :
C l — £ ^ a , 4
b l — £ p b . 4
Проинтегрируем эту систему дифференциальных уравнений, учтем краевые условия (7), (8) и найдем
pa
—
4 ω 1 0 εT ,
Pb =
—
4 ω 2 0 εT ,
а затем решение системы (37). Это решение описывается выражениями (23). Из соотношений (11), (14), (36), (38) следует, что
* p cos(^ — a + y ) и —-------------—
_ p
a
cos
(
^
—
a
)
—
pb
sin
( — a) _ = 2 — a10 cos(^ — a)+ a0 sin (^ — a) εT . Воспользуемся формулами (25), (39) и найдем оптимальное управление в форме синтеза u Q m1 cos a + m2 sin a 2 ST-t) Отметим, что при T _ T2 приходим к выражению (34), а при T > T2 управление и * удовлетворяет неравенству - и0< и * < и0. Оптимальные управления и^, и2 и определяются из соотношений (28), в которые следует подставить и * из (40). Вычислим минимальные затраты энергии, используя соотношения (30), (40) j_ 2m εT . Угловые скорости m1 (t), m2 (t) при всех T _ T1, T1 < T< T2, T > T2 выражаются формулами (25). Примеры Рассмотрим задачу оптимального управления экваториальной составляющей угловой скорости твердого тела из начального состояния m1 (0) _ 0,5, m2 (0)_ 0,543 в конечное положение (2). Предполагается, что отношение главных центральных моментов инерции твердого тела I _ 2, малый параметр s _ 0,1, угол a _ 30°, предельное значение управления и0 _ 1, а осевая составляющая угловой скорости изменяется по линейному закону m3(t) _ 0,081. Положим T _ 17. Для определения оптимального решения воспользуемся формулами (25), (29)–(31) и найдем угловые скорости, оптимальное управление, минимальные энергетические затраты. На рис. 1 представлены графики зависимостей угловых скоростей m1, m2 и управления и * от времени. Моменты переключения оптимального управления и * соответственно равны т1 _ 2,908, т2 _ 6,626, т3 _ 9,327, т4 _ 11,065, т5 _ 12,866, т6 _ 14,177, т7 _ 15,623, т8 _ 16,719. Минимальное значение функционала энергетических затрат равно J* _ 1,203. Рис. 1. T _ 17 Вычислим по формуле (32) момент окончания процесса T _ 5п (минимальное время, при котором еще возможен переход из заданного начального положения в конечное (2)). Оптимальное управление и * является кусочно-постоянной функцией: и *_-1 при t е[0,5,117]и [10,233,13,537] и и*_+1 при t е [5,117,10,233]и [13,537, 5п]; затраты энергии на управление равны J* _ 0,5п. На рис. 2 изображены графики, иллюстрирующие полученное решение. Рис. 2. T _ 5п Примем T _ 23. Для определения угловых скоростей, оптимального управления и энергетических затрат воспользуемся соотношениями (25), (40), (41). В этом случае оптимальное управление и *(t) является непрерывной функцией, при всех t е [0; 23]: - 0,870 < и * (t) < 0,870. Минимальные энергетические затраты равны J* _ 0,870. Графики зависимостей угловых скоростей m1 (t), m2 (t) и оптимального управления и*(t) приведены на рис. 3. Рис. 3. T = 23 Заключение В аналитическом виде получено приближенное решение задачи оптимального по энергетическим затратам управления гашением экваториальной составляющей угловой скорости динамически симметричного твердого тела. С использованием принципа максимума Л.С. Понтрягина и метода усреднения найдены оптимальные управления в форме синтеза, угловые скорости, минимальные значения функционала энергетических затрат при трех режимах реализации управления. Указано соотношение, при выполнении которого рассматриваемая задача решения не имеет. Представлены конкретные примеры построения оптимального решения при заданных граничных условиях.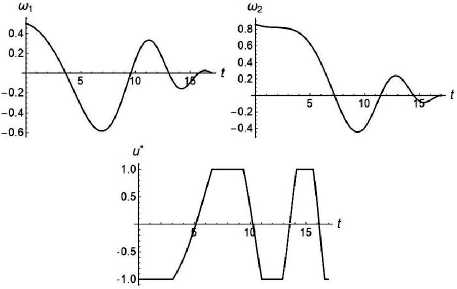
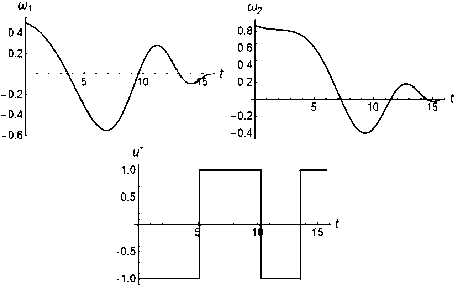
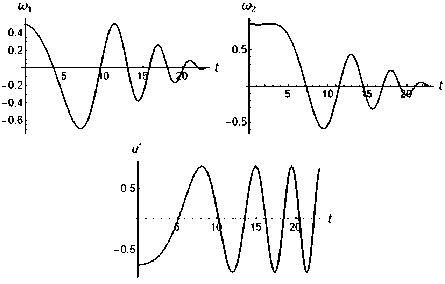
Список литературы К задаче об управляемых вращениях динамически симметричного твердого тела
- Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.
- Акуленко Л.Д. Асимптотические методы оптимального управления. М.: Наука, 1987. 368 с.
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976. 392 с.
- Атанс М., Фалб П. Оптимальное управление. М.: Машиностроение, 1968. 764 с.


