Качественное исследование системы дифференциальных уравнений на инвариантном треугольнике частот
Автор: Бортковская М.Р.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Функциональный анализ и дифференциальные уравнения
Статья в выпуске: 3, 2023 года.
Бесплатный доступ
В статье рассматривается 6-параметрическое семейство автономных систем обыкновенных дифференциальных уравнений, применяемых в классических моделях конкурентного взаимодействия трех групп представителей одной популяции. Такие системы могут использоваться для моделирования взаимодействия трех конкурирующих групп в задачах разной тематики. Системы рассматриваются на инвариантном треугольнике частот; исследование проводится для произвольных значений параметров, за исключением случаев их специальных соотношений. Дано определение множества приближения к особой точке (удаления от нее) относительно семейства отрезков. Исследуются границы этих множеств для особых точек, расположенных в вершинах треугольника частот.
Автономная система, обыкновенные дифференциальные уравнения, параметрическое семейство систем, трехмерная система, динамическая модель, особые точки, фазовый портрет системы, инвариантное множество, численный пример
Короткий адрес: https://sciup.org/148326988
IDR: 148326988 | УДК: 517.925.5 | DOI: 10.18101/2304-5728-2023-3-3-13
Текст научной статьи Качественное исследование системы дифференциальных уравнений на инвариантном треугольнике частот
Будем рассматривать систему трех дифференциальных уравнений вида x, = x •((Ax), - xTAx), i = 1,2,3,
' 0 . где A = у v£
< x i ( t ) )
a
Z
в"
5 — матрица с нулевыми диагональными элементами, 0 ,
x(t) = x2(t) — искомая вектор-функция. Система вида (1) с конкретны-v xз( t), ми числовыми значениями элементов матрицы A приведена в книге [1] как пример динамической модели конкуренции представителей трех групп в пределах популяции животных одного вида. Также система такого вида применялась автором данной статьи для моделирования конкуренции трех групп личных имен в русском языке (см. [2]). Система (1) рассматривается на инвариантном треугольнике частот
^ x = 1; x > 0> (x (t) — относительная частота в популяции пред-tT i i i ставителей i -й конкурирующей группы в момент времени t). Ненулевые элементы матрицы A естественно рассматривать как параметры, а множество систем вида (1) с произвольными значениями параметров как параметрическое семейство систем. В книге [1] разбирается численный пример модели конкуренции в популяции и объясняется, почему в такой модели всегда можно, не умаляя общности, считать диагональные элементы матрицы A нулевыми, а также утверждается инвариантность D относительно системы (1), которую легко проверить непосредственно (см. [2]).
1 Постановка задачи
В настоящей статье рассмотрим особые точки системы (1), которые могут в зависимости от значений параметров а , в , у , 5 , £ , £ возникать внутри и на сторонах треугольника частот D (его вершины — особые точки системы (1) при любых значениях параметров); исследуем (предварительно дав необходимые определения) множества приближения к особым точкам и удаления от них для особых точек системы (1), находящихся в вершинах треугольника частот; разработаем способ нахождения уравнений кривых - границ множеств приближения (удаления) и исследуем геометрическое расположение найденных кривых по отношению к особым точкам системы (1). Цель работы: не решая систему численно, изучить качественно ее фазовый портрет на треугольнике частот для произвольных значений параметров системы, за исключением особых случаев (когда параметры связаны специальными соотношениями), выделить такие случаи. После доказательства общих утверждений и описания способа нахождения границ множеств приближения к особым точкам (удаления от них) рассмотрим пример с конкретными числовыми значениями параметров системы (1), иллюстрирующий результаты исследования.
2 Особые точки системы (1)
Как уже отмечено, вершины инвариантного треугольника частот D являются особыми точками системы (1) при любых значениях параметров, что легко проверяется. Эти особые точки всегда сложные (матрица линеаризованной системы в этих точках имеет по крайней мере одно нулевое собственное число). На стороне треугольника частот { x 3 = 0, X ] + x 2 = 1, x i > 0, i = 1,2} в случае, когда ау > 0, имеется особая
I ay I точка I-----,-----,0 I. Она простая (седло либо узел), если
^ a + у a + у J yZ + as - ay * 0. Если ay = 0 , a2 + у2 * 0, то эта особая точка сложная и совпадает с вершиной треугольника частот. Если ay < 0 или a2 + у2 = 0, то на соответствующей стороне треугольника D также нет особых точек системы (1), за исключением вершин треугольника. Анало-
§ z I гично рассматриваются особые точки 0;----;---- и
( § + Z § + Z )
в п е I
----;0;---- , которые при соответствующих значениях параметров
в + е в + е / имеются на двух других сторонах треугольника частот (подробно об этом в статье [2]). Стороны треугольника D в свою очередь являются инвариантными множествами системы (1), и на них легко из вида правых частей системы (1) определить направления движения. Исследование возможных сложных особых точек здесь не проводится, но из дальнейших рассуждений будет видно, что в ряде случаев оно может и не понадобиться для получения качественного фазового портрета системы (1) на D.
Теорема 1. Для того чтобы точка N (х1, х2, х3), такая, что х1 > 0, х2 > 0, х3 > 0, была особой точкой системы (1), расположенной внутри треугольника частот D , необходимо и достаточно, чтобы ее координаты х1, х2, х3 удовлетворяли системе линейных алгебраических уравнений ax 2 + вх3 = YX) + §х 3,
< е х 1 + Z x 2 = у Х ) + § х 3, (2)
X j + х 2 + х 3 = 1.
Доказательство. Система (2) получается приравниванием нулю правых частей системы (1) при условиях х1 ■ х2 ■ х3 * 0 и х1 + х2 + х3 = 1. Отсюда очевидна необходимость заявленного в теореме условия неподвижности точки N. Докажем его достаточность. Пусть х1,х2, х3 - решение системы (2). Тогда имеем ух1 + §х3 = (ух1 + §х3) ■ ^ хi = ух1 + §х1 х3 + ух1 х2 + §х2х3 + ух1 х3 + §х3 .
i = 1
Это равенство, поскольку в силу системы (2) ух1 = aX2 + вх3 - §х3 и §х3 = ех1 + ZX2 - ух1, означает, что ул:1 + §х3 = х1 (a:%2 + вх3 - §х3) + §:х15с3 +
+ ух: 1 х2 + § х2х3 + у х % 1 х 3 + х3( е х 1 + ^ х2 - у ^%1 )-
Отсюда y x1 + 3 x 3 = x 1( a x 2 + ^ x 3) + x 2( / x 1 + 3 x 3) + x 3( £ x 1 + Z x 2) = x T Ax , а поскольку в силу системы (2) верны равенства y x1 + 3 x3 = a x2 + P x3 = s x1 + £ x 2, то будут верны и равенства a x2 + P x3 = x T Ax и £ x1 + £ x2 = x T Ax , то есть в точке N все правые части системы (1) обратятся в нуль. Теорема доказана.
Замечание 1 . Вычислив определитель системы (2), получаем, что при условии ( у + 3 )( -3 - Z ) — ( / — £ + Z )( — а + в - 3 ) * 0 система (1) может иметь внутри D не больше одной особой точки.
Замечание 2 . Легко убедиться, что, если система (2) имеет такое решение, что две его компоненты (координаты) положительны, а третья равна нулю, то это решение совпадает с координатами одной из особых точек системы (1), лежащих на сторонах (но не в вершинах) треугольника D , найденных ранее.
-
3 Границы множеств приближения к особым точкам и удаления от особых точек системы (1), расположенных в вершинах треугольника частот
Пусть { 1 C } , 0 < C < 1, — непрерывное однопараметрическое семейство отрезков параллельных прямых; все отрезки лежат в треугольнике частот D и через каждую внутреннюю точку D проходит ровно один отрезок. Пусть P - особая точка системы (1), расположенная в вершине треугольника D , и имеет место следующее: каждый луч, исходящий из точки P , 3
лежащий в плоскости ^ xz = 1 и направленный внутрь D , пересекает ка- i = 1
ждый отрезок lC ровно в одной точке, причем значения C , соответствующие пересекаемым лучом прямым, меняются вдоль луча строго монотонно.
Определение 1. Такое семейство отрезков { lC } будем называть правильным по отношению к особой точке P .
Пусть точка P и семейство отрезков { lC } таковы, как в определении 1. Пусть для определённости при движении вдоль каждого луча, исходящего из точки P , значения C убывают. Рассмотрим точку T внутри D , она лежит на некотором (единственном) отрезке lC e { lC } . Пусть траектория системы (1), проходящая через точку T , имеет участок d , содержащий внутри точку T и такой, что при движении по этому участку траектории в соответствии с системой (1) значения C при пересечении d c отрезками { lC } строго возрастают.
Определение 2. Такую точку T назовем точкой приближения к особой точке P относительно правильного семейства отрезков { lC } . (В этом определении, очевидно, можно поменять местами убывание и возрастание 6
параметра C вдоль произвольного луча, исходящего из P , и вдоль участка траектории, проходящей через T , соответственно).
Аналогично определим точку удаления от особой точки P относительно семейства отрезков { lC } .
Определение 3. Плоское множество G с D , состоящую из точек приближения к особой точке P (удаления от особой точки P ) относительно правильного семейства отрезков { lC } , назовем, соответственно, множеством приближения (удаления) точки P относительно этого семейства отрезков.
Ниже, если оговорено, о каком правильном семействе отрезков идет речь, будем для краткости называть множества приближения к особой точке (удаления от нее) относительно этого семейства просто множествами приближения (удаления) особой точки.
Теорема 2. Пусть Y 1 — пересечение внутренности int D треугольника 3
частот D с кривой у 1 , лежащей в плоскости ^ xt = 1, и такой, что ее про- i = 1
екция на плоскость x 1 Ox 2 задается уравнением второго порядка ( в + £ ) x 1 2 + ( 5 + Z ) x 2 + ( -a - Y + в + 5 + £ + Z ) x 1 x 2 +
+(-2в - £)x1 + (a - в - 5 - Z)x2 + в = 0.
Тогда Y разделяет множество приближения к особой точке S 1 (1;0;0) и множество удаления от особой точки S 1 (1;0;0) системы (1) относительно некоторого правильного семейства отрезков , если только данное уравнение второго порядка не задает прямую, точку или пустое множество.
Если Y 1 n int D = 0 , то int D — множество приближения или множество удаления особой точки S 1.
Доказательство . Рассмотрим всевозможные плоскости, задаваемые уравнениями x 2 + x 3 = C , 0 < C < 1. Их пересечения с инвариантным треугольником D — множество отрезков, параллельных стороне треугольника D , противолежащей вершине S 1 (1;0;0) (особой точке из формулировки теоремы 2). Ясно, что это множество отрезков — правильное семейство отрезков по отношению к S 1 . Если траектория системы (1), проходя через точку P , лежащую внутри D на одном из этих отрезков, пересекает с ростом времени t данный отрезок «в направлении» роста значений C , то точка P лежит в множестве удаления от особой точки S 1 , а если траектория пересекает этот отрезок «в направлении» убывания значений C , то точка P лежит в множестве приближения к особой точке S 1 . Точки внутри D , лежащие на границе множеств приближения и удаления особой точки S 1 , могут быть только такими, в которых обращается в нуль производная функции x 2 + x 3 в силу системы (1). Поскольку мы 7
исследуем систему (1) на треугольнике D , это то же самое, что найти все точки внутри D , в которых обращается в нуль производная функции x = 1 - ( x 2 + x 3) в силу системы (1). Приравняв нулю правую часть первого уравнения системы (1) и подставив в полученное равенство x 3 = 1 - X j - x 2, получим уравнение второго порядка из формулировки доказываемой теоремы. При переходе точки плоскости x 1 Ox 2 через соответствующую кривую второго порядка производная функции x 1 в силу системы (1) меняет знак, за исключением вырожденных случаев, оговоренных в условии теоремы. Если кривая второго порядка не пересекает треугольник { x , > 0, x 2 > 0, x j + x 2 < 1}, то вся int D — множество приближения или множество удаления особой точки S 1 . Теорема доказана.
Замечание 3 . Аналогично можно получить границу множеств приближения и удаления для двух других особых точек S 2(0;1;0); S 3(0;0;1) системы (1), расположенных в вершинах треугольника частот (относительно семейства отрезков, параллельных стороне треугольника, противолежащей изучаемой особой точке).
Замечание 4 . Где именно по отношению к у , будет множество приближения, а где множество удаления, легко понять по знаку левой части полученного в теореме 2 уравнения второго порядка.
Замечание 5 . Для построения фазового портрета системы (1) удобно для всех особых точек, расположенных в вершинах D , спроецировать границы множеств приближения и удаления относительно соответствующих семейств прямых на одну и ту же координатную плоскость (неважно, на какую). Ниже в числовом примере для особых точек S 2(0;1;0) и S 3(0;0;1) обозначим соответственно как у 2 и у 3 кривые, аналогичные кривой / j для точки S 1 , и выпишем уравнения проекций этих кривых на плоскость x j Ox 2. В общем виде их также легко записать.
Замечание 6 . Рассмотрение линий уровня функции x 2 + x 3 и исследование ее монотонности вдоль траекторий системы (1) опирается на идеи второго метода Ляпунова ([3], [4]). Но здесь мы не исследуем как таковую устойчивость особой точки. Рассуждения, подобные примененным в доказательстве теоремы 2, демонстрируются в книге [1] с помощью числового примера, где рассмотрены линии уровня нелинейной функции, там такой подход назван рассуждениями «типа Ляпунова».
Теорема 3 . Кривая у i , i = 1,2,3, разделяющая в D множества приближения и удаления одной из особых точек Si системы (1), рассмотренные выше, проходит через особые точки системы (1), которые являются внутренними точками сторон треугольника D , смежных с вершиной Si , если такие особые точки существуют.
Доказательство. Рассмотрим для определенности S 1(1; 0; 0). На смежных с этой вершиной сторонах треугольника частот могут быть особые ( В „ £ 1 z точки системы (1): К\-----,0,----- (если только в£ > 0) и
( в + £ в + £ )
I a Y ^1/
M I----- ,-----, 0 I (если только ay > 0). Для того, чтобы убедиться, что
(a + у a + у J кривая Y1 проходит через эти точки, достаточно убедиться, что ее проек ция на координатную плоскость х1Ox2 проходит через проекции точек K и M на эту плоскость, поскольку на D любые две координаты точки од-3
нозначно определяют точку в силу равенства ^ х = 1. Подставим i = 1
Х =---- , х2 = 0 в уравнение второго порядка из теоремы 2, получим
1 в + £ 2
в2 (2в + £) в п Л в £ 1 „ п
----+ в = -в •--+----- + в = 0, то есть у, проходит в + £ в + £ I в + £ в + £)
через точку K .
Аналогичные выкладки показывают, что кривая Y проходит через точку M. Для вершин S2, S3 доказательство полностью аналогично. Теорема доказана.
Теорема 4. Пусть кривая у i , i = 1,2,3, разделяет в D множества приближения и удаления одной из особых точек S i , i = 1,2,3, системы (1), рассмотренные выше. Если N (х, Х 2, Х 3) — особая точка, расположенная внутри треугольника частот D , то кривая у i , i = 1,2,3 проходит через точку N .
Доказательство. Для определенности рассмотрим кривую х, разделяющую множества притяжения и отталкивания особой точки S 1 (1; 0; 0). Кривая Y является пересечением поверхности второго порядка ( Ах )1 - хт Ах = 0 и треугольника D . Из доказательства теоремы 1 видно, что точка N ( х % 1, Х 2, Х 3) принадлежит тому же пересечению. Для кривых / 2, / 3 доказательство аналогично. Теорема доказана.
Замечание 7. Если кривая х не содержит внутренних точек треугольника частот, то и особых точек, расположенных внутри D , система (1) не имеет. Обратное неверно.
Замечание 8. Изучение особых точек параметрического семейства систем можно продолжить с помощью методов теории бифуркаций. В работах такой тематики, где рассматривается динамическое моделирование с помощью систем дифференциальных уравнений, можно встретить применение термина «неподвижная точка» для особой точки (положения равновесия) системы дифференциальных уравнений ([5]). Это понятие отлично от понятия неподвижных (в отличие от подвижных) особых точек решений дифференциальных уравнений ([6], [7]), также применяемого в задачах динамического моделирования.
-
4 Числовой пример
Рассмотрим систему (1), где параметры имеют следующие значения: a = 11,4, в = - 1,2, у = 3,4, 5 = 5,4, s = - 2,4, Z = 12,7 . Она получена в работе [2] при построении модели конкуренции трех групп женских личных имен в русском языке. Здесь а/ > 0, 5£ > 0, ps > 0, и на сторонах треугольника частот, помимо его вершин, есть особые точка системы (1): K (0,3;0;0,7) (неустойчивый узел), L (0; 0,3; 0,7) и M (0,8;0,2;0) (устойчивые узлы); координаты точек даны приближенно (с округлением); тип точек определяется по первому приближению. Внутри треугольника частот одна особая точка N (0,342; 0,306; 0,352) (трехмерное седло), найденная в соответствии с теоремой 1. Уравнения проекций на плоскость х 1 Ox 2 границ множеств приближения и удаления для особых точек системы (1), расположенных в вершинах треугольника, ищем согласно теореме 2 и замечанию 3:
-
1. - 3,6 X ] 2 + 18,1 х 2 - 0,3 X ] х 2 + 4,8 X ] - 5,5 х 2 - 1,2 = 0 ( у ' 1 , проекция / 1 ) для 5 1(1;0;0);
-
2. - 3,6 х 1 2 + 18,1 х 2 - 0,3 х 1 х 2 + 1,6 х 1 - 23,5 х 2 + 5,4 = 0 ( у '2,проекция у 2) для 5 2 (0; 1; 0);
-
3. - 3,6 х 2 + 18,1 х 2 - 0,3 х 1 х 2 + 1,2 х 1 - 5,4 х 2 = 0 ( у '3, проекция / 3) для 5 3 (0; 0; 1). (Все три кривые -гиперболы, см. рис.1).
На рисунке 1 точка K ' — проекция точки K на плоскость х 1 Ох 2, L ' — проекция точки L и так далее. На рисунке 2 изображены кривые Y 1 , / 2, / 3 и несколько траекторий системы (1) (стрелками указано направление движения по траектории).
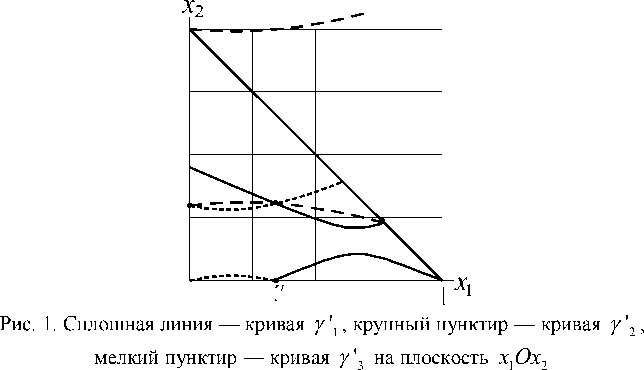
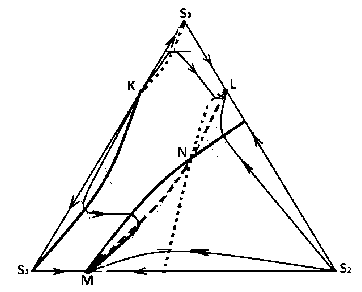
Рис. 2. Сплошная жирная линия — кривая γ % 1 , крупный пунктир — кривая γ % 2 , мелкий пунктир — γ % 3 . Сплошные линии со стрелками — траектории системы (1)
Рисунки 1 и 2 иллюстрируют утверждения теорем 2, 3 и 4.На рисунке 3 приведен качественный фазовый портрет системы, обобщающий полученные результаты.
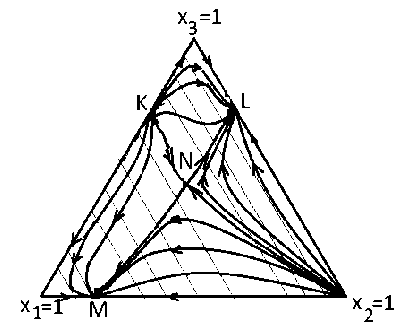
Рис. 3. Фазовый портрет системы из примера
Заключение
Полученные результаты позволяют анализировать поведение траекторий системы (1) не только качественно, но и численно, за исключением специальных (вырожденных) случаев, когда параметры системы связаны определенными соотношениями, отмеченными в статье. В остальных случаях, зная координаты любой неособой точки треугольника частот, мы можем установить поведение проходящей через эту точку траектории по отношению к любой особой точке системы (1), расположенной в одной из вершин треугольника частот, а именно, — указать, в каком из множеств (приближения или удаления) по отношению к данной особой точке расположена выбранная точка. Этот факт удобно использовать для сравнения эспериментальных данных с результатами моделирования, применяя системы вида (1) для динамического моделирования процессов конкуренции. Теоремы о взаимном расположении множеств приближения (удаления) и особых точек системы (1) помогают построить фазовый портрет системы на треугольнике частот. Перспектива дальнейшего исследования системы (1) состоит в дополнительном рассмотрении вырожденных случаев (возможно с помощью методов теории бифуркаций), а также в применении метода, разработанного в настоящей статье, для нахождения границ множеств приближения и удаления для особых точек, не расположенных в вершинах треугольника частот. Поскольку модели популяционной динамики используются для моделирования процессов конкуренции в различных областях ([8], [9]), исследование системы (1) имеет прикладную актуальность.
Список литературы Качественное исследование системы дифференциальных уравнений на инвариантном треугольнике частот
- Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями: пер. с англ. Москва: Мир, 1986. 248 с.
- Бортковская М. Р. Пример моделирования конкуренции в языке с помощью системы дифференциальных уравнений // Анализ, моделирование, управление, развитие социально-экономических систем (Амур-2022): сборник научных трудов XVI Всероссийской с международным участием школы-симпозиума. Симферополь, 2022. С. 74-79.
- Бибиков Ю. Н. Курс обыкновенных дифференциальных уравнений: учебное пособие для ун-тов. Москва: Высшая школа, 1991. 303 с.
- Демидович Б. П. Лекции по математической теории устойчивости: учебное пособие для вузов. Санкт-Петербург: Лань, 2023. 480 с.
- Лукин Д. С., Гайдук А. Р. Исследование нелинейной системы с бифуркацией // Математические методы в технологиях и технике. 2021. № 2. С. 7-10.
- Арнольд В. И., Ильяшенко Ю. С. Обыкновенные дифференциальные уравнения // Итоги науки и техники. Сер. Современные проблемы математики. Фундаментальные направления. 1985. Т. 1. С. 7-140.
- Орлов В. Н., Гасанов М. В. Влияние возмущения подвижной особой точки на структуру аналитического приближенного решения одного класса нелинейных уравнений на инвариантном треугольнике частот дифференциальных уравнений третьего порядка в комплексной области // Вестник МГТУ им. Н. Э. Баумана. Сер. Естественные науки. 2022. № 6. С. 60-73.
- Макаренко С. И. Динамическая модель двунаправленного информационного конфликта с учетом возможностей сторон по наблюдению, захвату и блокировке ресурса // Системы управления, связи и безопасности. 2017. № 1. С. 60-89.
- Альрефаи В. А. Моделирование и численный анализ динамических систем с конкурентным взаимодействием // Технологический аудит и резервы производства. 2015. № 2/5(22). С. 36-41.


