Как определить кадастровую стоимость

Поводом для написания настоящей статьи послужила публикация профессора С.П. Коростелева [1], в которой справедливо и заслуженно анализируются проблемы методологии кадастровой оценки недвижимости. Также в указанной работе подробно рассмотрены организационные и нормативные проблемы, которых мы не будем касаться в настоящей статье. Мы же обратим внимание на фундаментальную причину существования некоторой недосказанности и незавершенности в методологии кадастровой оценки, проникших в нормативные документы, а также изложим наш взгляд на то, как можно разрешить противоречия, накопившиеся как в нормативной базе, так и в методологии.

Чаще всего задачей оценки является определение «некоторой» стоимости объекта (рыночной, инвестиционной, ликвидационной, кадастровой и т. д.) до совершения сделки, то есть в условиях неопределенности. Таким образом, оценщик, хочет он того или нет, имеет дело со статистическими наблюдениями генеральных совокупностей, являющихся случайными величинами. Функции распределения этих случайных величин неизвестны. С одной стороны, задача оценки функции распределения генеральной совокупности является в достаточной степени сложной, с другой – нет необходимости ее решать, поскольку требования к функциям распределения весьма затруднительно заложить в стандарты и федеральные законы. В связи с этим приходится использовать достаточно информативные с вычислительной точки зрения числовые характеристики случайных величин 1. Из всех видов стоимости в Федеральном законе от 29 июля 1998 года № 135-ФЗ [2] только для рыночной указана числовая характеристика, которая должна быть определена – точка максимума плотности распределения цен 2. Все остальные виды стоимости не «привязаны» ни к каким числовым характеристикам, именно поэтому их определение связано с техническими сложностями – отсутствует прямое указание, что именно следует оценивать. В большинстве случаев спасает «привязка» к рыночной стоимости. Так было и с кадастровой стоимостью (далее также – КС), поскольку в 2014 году она определялась как рыночная, полученная методами массовой оценки на дату оценки.

Однако такая формулировка исчезла из Федерального стандарта оценки «Цель оценки и виды стоимости» № 2, и теперь для КС осталось только утверждение, что это стоимость для исчисления налоговых платежей. Естественно, что часть аналитиков испытывает огромное облегчение – возникает иллюзия, что не надо обосновывать способ расчета. Также возникает иллюзия, что ставкой налога можно будет отрегулировать возникающие противоречия. Это, конечно, не так.

Прежде всего возникает вопрос: если у двух объектов примерно одинаковая рыночная стоимость, то должны ли быть примерно одинаковыми суммы уплачиваемых налогов?

Представляется, что в условиях рыночной экономики, при соблюдении принципа некоторой справедливости ответ на этот вопрос должен быть положительным. Но тогда кадастровая стоимость неизбежно должна исчисляться как рыночная либо иметь некоторый обоснованный мультипликатор, применяемый к рыночной стоимости. В противном случае у кадастровых оценщиков не будет единого ориентира, и это будет приводить к диспропорциям в общей картине кадастровых стоимостей – будут возникать ситуации, когда объекты имеют разную кадастровую стоимость, разное налогообложение, а в реальности на рынке стоить одинаково.

Второй отправной точкой для написания настоящей статьи стала проделанная в Российской Федерации выдающаяся по трудозатратам и результатам работа по кадастровой оценке. В стране, наконец, создана основа для формирования обширных баз данных объектов недвижимости, содержащих кадастровые и рыночные данные, ценообразующие факторы. Вместо привычных одномерных случайных величин объектом изучения становятся многомерные случайные величины.

Ранее О.В. Русаковым (см. [3, 4]) было доказано, что цены, образованные последовательными сравнениями в условиях совершенной конкуренции, стремятся к формированию логарифмически нормально распределенной генеральной совокупности. Исследования распределений цен предложений и цен сделок как в Российской Федерации, так и за рубежом подтверждают этот теоретический результат 3 (см. [5–7]). Кроме того, логарифмически нормальное распределение удобно и с вычислительной точки зрения – точность определения точки максимума превышает принятую до сих пор точность оценки традиционными методами, а логарифмирование цен приводит аналитика к необходимости работать с привычным и хорошо изученным нормальным законом распределения 4.

Поскольку есть основания считать, что цены и предложений, и сделок имеют логарифмически нормальные распределения, любопытно было бы посмотреть, получился ли такой же тип распределения при кадастровой оценке.

На сайте Комитета имущественных отношений Санкт-Петербурга опубликован приказ от 27 августа 2015 года № 59-п «Об утверждении результатов определения кадастровой стоимости помещений площадью менее 3 000 кв. м на территории Санкт-Петербурга».

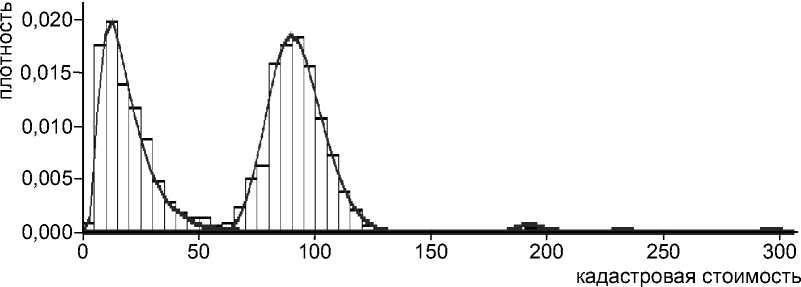
Рис. 1. Распределение кадастровой стоимости 1 квадратного метра нежилой недвижимости (в тыс. р., площадь – до 3 000 кв. м) в городе Санкт-Петербурге по результатам кадастровой оценки от 2014 года (утверждено в августе 2015 года). Гистограммы – эмпирические частоты, линии – кривые плотностей логарифмически нормальных распределений

В приложении № 2 к этому приказу содержится перечень всех объектов нежилой недвижимости, площадью до 3 000 квадратных метров. Всего в списке 472 645 объектов. На рисунке 1 показаны эмпирические частоты и приближающие их кривые плотностей логарифмически нормальных распределений с разными параметрами.

Приведенный рисунок является дополнительным аргументом для предположения о наличии логарифмически нормального распределения кадастровых стоимостей внутри групп (типов) объектов недвижимости. Этот факт не является удивительным, учитывая, что рыночная стоимость должна подчиняться такому закону, а кадастровая стоимость рассчитывалась как рыночная, определенная методами массовой оценки на конкретную дату коллективом высококвалифицированных оценщиков. В то же время на рисунке 1 отчетливо видны всего пять групп разных объектов. Объекты, относящиеся к разным группам, имеют существенные отличия по ценообразующим факторам. Внутри групп, скорее всего, чрезмерно строгий учет ценообразующих факторов не приведет к перемещению объекта из одной группы в другую. По состоянию на 2014 год в Санкт-Петербурге в классе «встроенная коммерческая недвижимость» выделено всего пять значимо различных кластеров. Таким образом, можно считать, что всю выборку (здесь – по городу Санкт-Петербургу) можно разбить на пять групп, каждая из которых будет распределена по логарифмически нормальному закону.

Рассмотрим двумерную случайную величину ( V_кс ,V_цп ) ( V_кс – кадастровая стоимость, V_цп – цена предложения). Пусть V_кс ,V_цп имеют логарифмически нормальные распределения с параметрами μ ₁ , σ ₁ (для кадастровой стоимости) и μ ₂ , σ ₂ (для цен предложений) соответственно. Справедливо следующее утверждение, ранее доказанное в работах [9, 10]: если случайные величины V_кс и V_цп имеют совместное логарифмически нормальное распределение, то при фиксированном V_кс = v наиболее вероятная цена V_рс (рыночная стоимость) равна:

V pc = Mode ( V „„| V .c = V

) = exp ц 1 + p— ( Inv - ц ₂ )

’ L        ^ 2

^^^^^^^е

12 ( ^{1 -} p ² ) ,

где ρ – коэффициент корреляции.

Формула (1) дает ключ к пониманию, как при имеющемся массиве данных о ценах предложений (рыночная информация) можно пересчитать кадастровую стоимость так, чтобы она соответствовала текущему состоянию рынка 5. Однако в периодах между плановыми пересмотрами кадастровой стоимости эту формулу можно использовать для оценки текущей рыночной стоимости объекта (в приведенных единицах). Такая возможность появилась совсем недавно, после завершения кадастрового учета и присвоения кадастровых стоимостей. Более того, это создает совершенно новую реальность в оценке – при создании обширных баз данных появится возможность по кадастровому номеру объекта немедленно, основываясь на рыночных данных, оценить его рыночную стоимость. Учет ценообразующих факторов в традиционном понимании становится ненужным, так как он перемещается на стадию формирования выборки (приблизительно однородных объектов). В укрупненном виде это уже сделано при определении кадастровой стоимости. Как будет видно из приведенного далее примера 2, это не отменяет возможности более детального учета ценообразующих факторов при формировании выборки.

Из формулы (1) легко увидеть, что зависимость рыночной стоимости (далее также – РС) от кадастровой имеет вид степенной функции 6:

V рс = Mode ( V цп V кс = v ) = Av ^{ρσ 2}

где A = exp

μ ₁- ρ^{σ 1} μ ₂- σ ₁ ² ( 1- ρ ² ) σ ₂

Аналогичная формула может быть записана и для пары V_кс, V_цс (цена сделки). Тогда, получая оценку рыночной стоимости по ценам предложений (как функцию от кадастровой стоимости) и оценку рыночной стоимости по ценам реальных сделок (тоже как функцию от кадастровой стоимости), можно построить формулу для определения скидки на торг в каждом классе объектов недвижимости. Следует отметить, что скидка на торг тоже окажется степенной (не линейной и не константой!) функцией от кадастровой стоимости. Создание баз данных, включающих указанные поля, приведет к тому, что для оценивания скидки на торг не нужно будет знать, как объект продавался и как он был продан. По рыночной информации будут построены формулы вида (2) для оценки рыночной стоимости по ценам предложений и по реальным сделкам для скидки на торг. Далее для объекта оценки (не входит в выборку объектов сравнения) определяются кадастровый номер и кадастровая стоимость, затем проводятся оценки скидки на торг и рыночной стоимости.

Заметим, что формула (2) имеет «точку равновесия» – v ₀, удовлетворяющую следующему соотношению:

ρ^{σ 1}

v 0 = Av 0 ^{σ 2} .

В этой точке ( v ₀) кадастровая стоимость (как оценка рыночной стоимости по текущим рыночным данным) не изменится. В зависимости от знака коэффициента корреляции в одну сторону от точки равновесия (по числовой оси) кадастровая стоимость увеличится, в другую – уменьшится.

exp ^⎡_⎢⎣³₂× σ ₁ ² ( 1- ρ ² ) ^⎤_⎥⎦.

Рассмотрим два примера.

Пример 1

Выбор и подготовка данных

Для исследования использованы приложение № 1 к приказу № 59-п [8], содержащее информацию об адресах, кадастровых номерах и кадастровых стоимостях более 2 миллионов объектов жилищного фонда, Бюллетень недвижимости Санкт-Петербурга от 11 декабря 2017 года № 1809 с ценами предложений жилой недвижимости в 18 районах города (объем выборки – 2 823 наблюдения).

Если бы создатели рыночных баз данных при размещении объявлений указывали кадастровые номера, то объединение этих двух источников могло быть быстро сделано по кадастровым номерам. Пока такой возможности нет приходится использовать другие инструменты. Распределения цен предложений по районам города хорошо приближаются (удовлетворительные результаты теста Колмогорова-Смирнова) логарифмически нормальным законом распределения. Параметры законов представлены в таблице 1.

Таблица 1

Параметры нормальных законов распределения логарифмов цен предложений на жилую недвижимость в городе Санкт-Петербурге в декабре 2017 года (рассматриваются натуральные логарифмы цен в тыс. р. / кв. м)

Район	Параметры
	среднее	стандартное отклонение	коэффициент корреляции с кадастровой стоимостью
Адмиралтейский	4,668	0,266	0,533
Василеостровский	4,863	0,231	0,651
Выборгский	4,635	0,194	0,599
Калининский	4,586	0,183	0,703
Кировский	4,563	0,164	0,595
Колпинский	4,368	0,210	0,332
Красногвардейский	4,521	0,181	0,766
Красносельский	4,506	0,172	0,730
Кронштадтский	4,399	0,141	0,604
Курортный	4,673	0,276	0,422
Московский	4,730	0,223	0,673
Невский	4,534	0,143	0,738
Петродворцовый	4,364	0,088	0,410
Петроградский	5,019	0,540	0,900
Пушкинский	4,604	0,184	0,317
Приморский	4,657	0,176	0,654
Фрунзенский	4,545	0,161	0,725
Центральный	4,795	0,362	0,576

Четыре района (Красносельский, Фрунзенский, Невский, Красногвардейский) имеют близкие параметры. Проверим гипотезу о гомогенности (незначимости расхождений) средних и дисперсий. В таблице 2 приведены значения p-value для тестов Стьюдента, Флигнера-Киллина, Фишера.

Таблица 2

Значения p-value для тестов Стьюдента, Флигнера-Киллина, Фишера на значимость расхождения средних и дисперсий для выборок логарифмов цен предложений по Фрунзенскому, Красногвардейскому, Красносельскому, Невскому районам города Санкт-Петербурга

Пары районов	Значения p-value для тестов
	Стьюдента	Флигнера-Киллина	Фишера
Фрунзенский – Красногвардейский	0,433	0,7688	0,3822
Фрунзенский – Красносельский	0,2274	0,7677	0,6532
Фрунзенский – Невский	0,797	0,2667	0,4982

Поскольку p-value везде значительно превосходит 0,05, расхождения при 5-процентном уровне значимости несущественны, эти районы можно объединить в одну выборку.

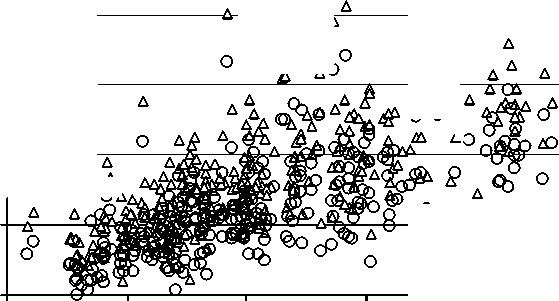
На рисунке 2 представлена объединенная двумерная выборка по указанным четырем районам: кадастровая стоимость – цена предложения.

В логарифмической плоскости облако рассеяния принимает характерный эллиптический вид, что является основанием для проверки статистической гипотезы на со- о

CD

A

О

as т m

A A о о лаА

до

О

Ф° о

A

A

кадастровая стоимость

Рис. 2. Эмпирическое распределение двумерной случайной величины кадастровая стоимость – цена предложения (в тыс. р./кв. м). Маркер «треугольник» – без учета скидки на торг, маркер «кружок» – с учетом постоянной скидки на торг 10 процентов

О

0,6

0,4

0,2

0,0

угол поворота, град

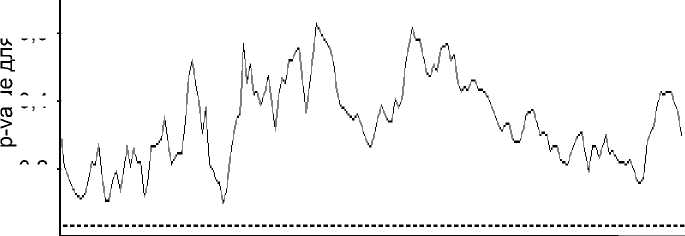
Рис. 3. Результат кругового теста Колмогорова-Смирнова на совместно нормальное распределение кадастровой стоимости и цены предложения для объединенной выборки (пунктиром обозначено критическое значение 5 процентов)

вместно нормальное распределение логарифмов кадастровой стоимости и цены предложения.

На рисунке 3 представлен результат кругового теста Колмогорова-Смирнова (см. [9, 10]) на совместную нормальность логарифмов.

Результат кругового теста Колмогорова-Смирнова по второй координатной оси аналогичен приведенному на рисунке 3, поскольку получается из него сдвигом по горизонтальной оси на π /2. Гипотеза о совместной нормальности логарифмов на 5-процентном уровне значимости не отвергается, так как при любом угле поворота от 0 до π кривая линия (значение p-value) не опускается ниже критического значения 5 процентов.

Приближение эмпирической плотности выборки двумерной совместно логарифмически нормальной поверхностью дает поверхность, представленную на рисунке 4, с параметрами р 1 = 4,5041; р 1 = 0,1119; р 2 = 4,5296; о ₂ = 0,1633; р = 0,7322.

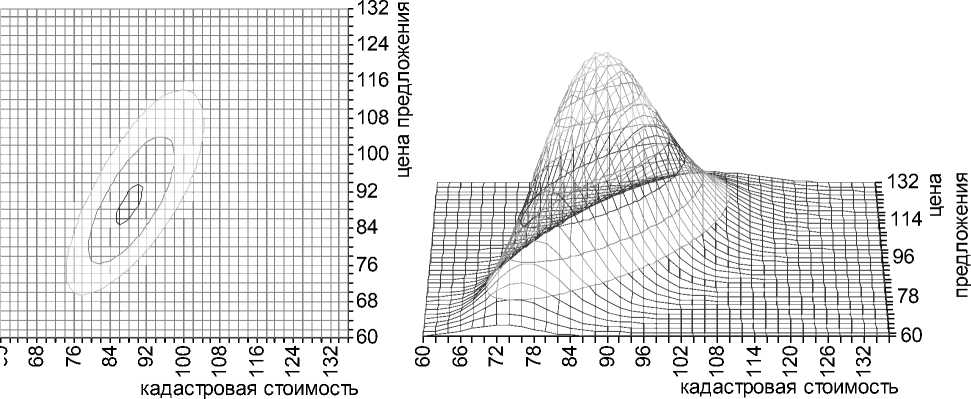
а)

б)

Рис. 4. Аппроксимация эмпирической плотности выборки двумерной совместно логарифмически нормальной поверхностью: а) вид проекции поверхности плотности на фазовую плоскость; б) вид поверхности в трехмерном измерении (по вертикали – плотность распределения). Размерность кадастровой стоимости и цены предложения – тыс. р./кв. м

Скидка на торг

В общем случае скидка на торг должна иметь вид степенной функции. В настоящее время информация о ценах сделок труднодоступна, поэтому мы пока отложим рассмотрение проблемы ее определения по статистическим данным. В то же время очевидно, что за последние годы рынок недвижимости сильно изменился и применение (для наглядности) постоянной 10-процентной скидки на торг выглядит даже оптимистично. При применении к ценам предложений такой скидки облако рассеяния незначительно изменится – все координаты по вертикальной оси уменьшатся на 10 процентов, произойдет вертикальное сжатие. Результаты кругового теста не изменятся. Двумерная теоретическая совместно логарифмически нормальная поверхность сместится. Значения параметров будут следующими: μ ₁ = 4,5041; σ ₁ = 0,1119; μ ₂ = 4,4243; σ ₂ = 0,1633; ρ = 0,7322.

Заметим, что изменилось только значение μ ₂ (уменьшилось на 0,1053, что соответствует мультипликатору 0,9, так как ln(0,9) = 0,1053). Подставляя эти параметры и параметры, полученные ранее для пары кадастровая стоимость – цена предложения, в формулу (2), получаем линии зависимости рыночной стоимости от кадастровой:

без учета скидки на торг:

V_рс = Mode ( V_цп V_кс = v ) = v ^{ρσ 21} exp

μ ₁- ρσ ¹ μ ₂- σ ₁ ² ( 1- ρ ² ) σ ₂

=0 , 743 v ^{1 , 068};

с учетом 10-процентной скидки на торг:

μ ₁- ρ^{σ 1} μ ₂- σ ₁ ² ( 1- ρ ² ) σ ₂

=0 , 669 v ^{1 , 068}.

^{ρ 1}

V_рс = Mode ( V_цп V_кс = v ) = v ^{σ 2} exp

Обе эти линии представлены на рисунке 5.

Точка равновесия

Разрешая уравнение v = 0,743 v ^1,068 относительно v , получим v = 78,927 (тыс. р. за 1 кв. м).

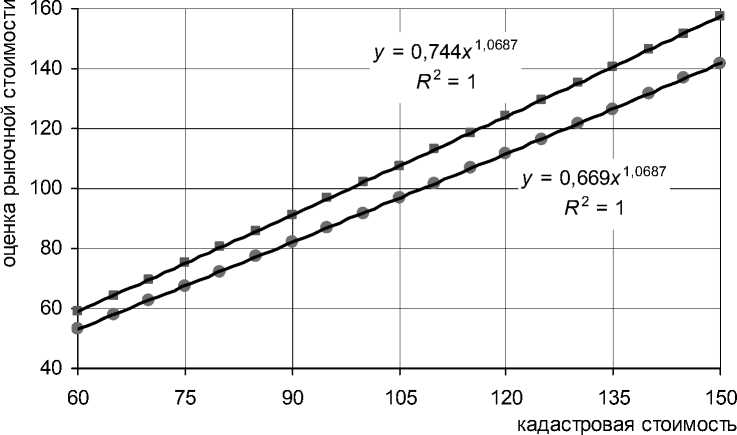
Рис. 5. Кривые зависимости рыночной стоимости от кадастровой (тыс. р./кв. м).

Верхняя линия – без учета скидки на торг, нижняя – с учетом 10-процентной скидки

Это кадастровая стоимость (КС), которая при преобразовании не изменится. КС ниже этого значения при пересмотре уменьшится, выше – увеличится.

Однако, если учесть скидку на торг в 10 процентов, то уравнение v = 0,669 v ^1,068 даст другое значение – точка равновесия сместится в v = 369,201 тысячи рублей за 1 квадратный метр, то есть смещение произошло в область значений КС, которые в рассматриваемых районах отсутствуют. Это означает, что для этих районов в области рассматриваемого диапазона кадастровых стоимостей новые кадастровые стоимости снизятся.

При изучении рисунка 5 возникает иллюзия, что можно было бы обойтись и линейным приближением. Однако это обманчивое впечатление, поскольку указанные зависимости имеют степенной характер, параметры зависят от пяти значений ( μ ₁, σ ₁, μ ₂, σ ₂, ρ ) и их вид может сильно отличаться от прямой линии. Для наглядности приведем результаты, рассчитанные для другой выборки.

Пример 2

Выбор и подготовка данных

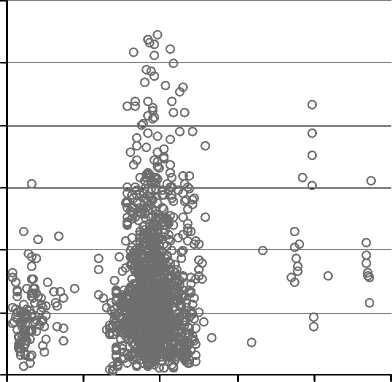
Для исследования использованы данные приложения № 2 к приказу № 59-п [8] (нежилой фонд площадью до 3 000 квадратных метров, адреса, кадастровые номера, кадастровые стоимости, объем выборки – 472 645 объектов) и данные о ценах предложений на такие объекты за 2012, 2013, 2014, 2015, 2016 годы из открытых источников. Цены предложений до 2015 года включительно скорректированы на время к 2016 году. На рисунке 6 представлена полученная объединенная выборка.

0     50    100    150    200    250

кадастровая стоимость

S8

_0

^5 с

1 23456

ln кадастровой стоимости

СК 600

т

CD

S 500 ct

Т

а)

б)

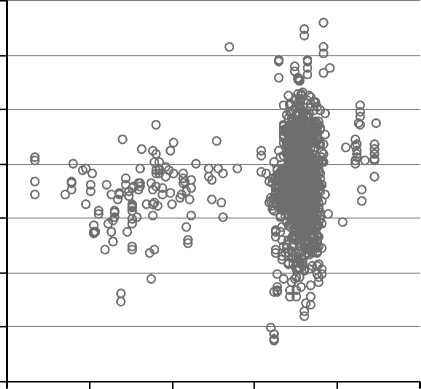
Рис. 6. Выборка двумерных пар кадастровая стоимость – цена предложения для коммерческой недвижимости в городе Санкт-Петербурге по состоянию на конец 2016 года: а) в натуральных единицах (тыс. р./кв. м), б) в логарифмической плоскости

На рисунке 6 видны три группы объектов, имеющих кадастровую стоимость (в тыс. р./ кв. м):

• 1)    до 50;

• 2)    от 50 до 150;

• 3)    свыше 150.

Третья группа еще недостаточно сформирована, поскольку в выборке мало предложений по дорогим объектам. В то же время выборка на рисунке 6 вполне соответствует выборке на рисунке 1 с пятью группами объектов. Следует ожидать, что при наращивании объема выборки сформируются еще три группы объектов, кадастровая стоимость которых превысит 150 тысяч рублей (~ 200, ~240 и ~300 тыс. р./кв. м).

Облака рассеяния по первой и второй группам объектов достаточно хорошо сформировались, в логарифмической плоскости имеют характерную эллиптическую форму и, как это хорошо видно на правой диаграмме, имеют разную направленность эллипсоидов рассеяния в направлении главных осей.

Были проведены все необходимые исследования, аналогичные приведенным для вторичной жилой недвижимости, в результате чего после удаления трех точек выбросов для первой группы получена удовлетворяющая статистическим тестам двумерная логарифмически нормальная поверхность. Для второй группы удовлетворительные логарифмически нормальные поверхности получаются после разделения группы на подвыборки по признаку «назначение объекта». После проведения всех необходимых преобразований получены зависимости рыночной стоимости от КС по формуле (2).

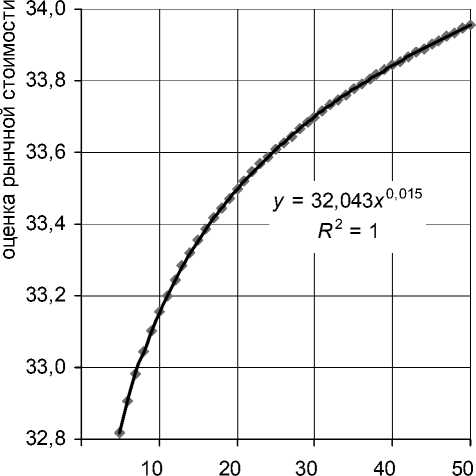
На рисунке 7 для примера показаны линии зависимости без учета скидки на торг для первой группы и для подвыборки «многофункциональные объекты».

кадастровая стоимость

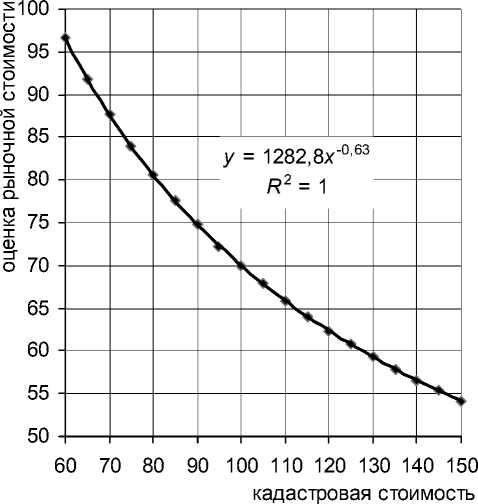
б)

Рис. 7. Зависимость рыночной стоимости от кадастровой (тыс. р./кв. м): а) для группы недорогих объектов (текущая КС – до 50 тыс. р.), б) для многофункциональных объектов без учета скидки на торг

а)

Для левой диаграммы точка равновесия определяется из соотношения v = 32,04 v ^0,014, решение этого уравнения дает значение v = 33,657 тыс. р./кв. м. Показанная на левой диаграмме формула указывает на увеличение кадастровой стоимости для всех значений «старой» КС ниже v = 33,657. Выше этого значения КС при пересчете уменьшится. Аналогично для правой диаграммы точка равновесия определяется из соотношения v = 1 282,83 v ^-0,63, решение этого уравнения дает значение v = 80,696 тыс. р./кв. м. В диапазоне до 80,696

тысячи рублей за 1 квадратный метр КС при пересчете увеличится, выше 80,696 – уменьшится. Эти вычисления не учитывают скидку на торг.

Скидка на торг объективно должна иметь вид степенной функции, о чем уже было сказано. Для ее качественного расчета необходимо располагать базами данных о реальных сделках. Тогда, сопоставляя зависимость РС от КС, определенную по ценам предложений, с зависимостью РС от КС, полученную по ценам сделок, можно получить формулу наиболее вероятной скидки на торг как функцию КС. В отсутствие таких баз приходится довольствоваться так называемыми экспертными опросами. Можно применить скидку на торг как постоянную (как это было сделано в примере для жилой недвижимости).

Период 2016–2017 годы вполне заслуженно можно было бы назвать периодом больших дисконтов. По нашим наблюдениям скидки на торг по коммерческой недвижимости достигали 20–30, а иногда 40 процентов. Также можно применить скидку на торг на основании подхода, изложенного в работе [11]. Однако, поскольку ее применение приводит к сужению области, в которой пересчитанная КС возрастает, мы воздержались от включения в настоящий материал расчетов, учитывающих скидку на торг.

Выводы

• 1.    В Российской Федерации проделана бесценная по значимости работа по кадастровому учету объектов недвижимости. В то же время в сформированных кадастровых базах накопилось большое количество неточностей, иногда ошибок, приводящих к дисбалансу при налогообложении. В настоящее время стоит задача пересчета КС с учетом рыночной информации, состояния рынка недвижимости, текущих макроэкономических условий.

• 2.    Отсутствует единая методология определения кадастровой стоимости. В нормативных документах нет прямых указаний на то, какие параметры законов распределения должны быть оценены. Отсутствует «привязка» кадастровой стоимости к рыночной, что при изменении макроэкономических условий, рынка, появлении новых объектов учета неизбежно будет приводить к новым противоречиям и дисбалансам при налогообложении. Кадастровая стоимость не может оставаться стоимостью, определяемой кадастровым оценщиком для целей налогообложения неизвестно каким способом. Должны быть выработаны единые принципы определения КС, что должно найти отражение в нормативных документах. Непротиворечивое определение КС возможно только при законодательном установлении связи кадастровой и рыночной стоимостей.

• 3.    В России впервые появилась уникальная возможность создания баз данных и методов расчета основных показателей рынка недвижимости, основанных на обширной рыночной статистике. Желательно включение кадастрового номера не только в государственные базы данных, но и во все частные базы, так как кадастровый номер выступает уникальным идентификатором объекта, по которому может быть установлена кадастровая стоимость, а по ней – рыночная стоимость по предложениям, по сделкам, оценена скидка на торг (даже при отсутствии рыночной информации на конкретный кадастровый номер). По кадастровому номеру могут быть оценены и другие важные показатели рынка недвижимости, такие как капитализация, ставки дисконтирования и многое другое.

• 4.    Традиционная задача учета ценообразующих факторов смещается в область формирования выборки объектов. Это задача требует определенных трудозатрат и аккуратности, так как выборка должна быть достаточно однородной (насколько это позволяет доступная аналитику (оценщику) информация о значимых ценообразующих факторах). Влияние ценообразующих факторов, которые невозможно вычленить из статистики, рассматривается как случайное.

• 5.    При статистическом подтверждении гипотезы о совместной логарифмической нормальности пересчет кадастровой стоимости, расчет рыночной стоимости, скидки на торг и других показателей, приводящих к сравнению параметров условных распределений, описывается степенными функциями.