Кинематический анализ движения дозируемого корма и расчет производительности спирально-тарельчатого дозатора

Объем и эффективность производства животноводческой продукции зависят от уровня кормления животных и сбалансированности рационов по питательным веществам [1; 2]. Важная роль в этом принадлежит устройствам и машинам, дозирующим компоненты комбикорма при их приготовлении в соответствии с рационами. Анализ дозирующих устройств показывает, что они не отвечают зоотехническим требованиям. По способу дозирования их делят на объемные и весовые. Использование весовых дозаторов в условиях сельскохозяйственного производства затруднено, поскольку их работа зачастую связана со средой повышенной влажности, с присутствием в ней аммиака, сероводорода и других вредных химических веществ. Значительные колебания температуры приводят к быстрому износу весоизмерительных механизмов и увеличению погрешности взвешивания. Для обслуживания и настройки на различные режимы работы таких устройств требуются высококвалифицированные специалисты [3].

В сельскохозяйственном производстве наибольшее применение получили объемные дозаторы с различными типами рабочих органов. Большинство из них удовлетворительно работают лишь с материалами легкой и средней текучести, но их нельзя рекомендовать для дозирования плохотекучих материалов.

Один из возможных трендов для устранения этих недостатков в объемных дозаторах, особенно сводов насыпных материалов в бункерах и дозаторах, на наш взгляд, – в использовании не только различных по конструкции сводообрушителей [4], но и вибрационных технологий и технических средств [5–7]. Если правильно подобрать все параметры объемного дозатора, выбрать рациональную конструкцию дозирующего рабочего органа и точно его отрегулировать в соответствии с тем количеством кормового материала, которое должно поступать за определенное время, такой дозатор будет вполне приемлем для механизации кормоприготовления [8]. Поэтому многими научно-исследовательскими и опытно-конструкторскими организациями страны ведется интенсивная работа по совершенствованию существующих средств механизации дозирования и созданию новых дозирующих устройств.

Объекты и результаты исследований

В данной работе нами предложен объемный дозатор спирально-тарельчатого типа (рис. 1). Состоит из бункера 1 , цилиндра 2 , внутри которого при помощи кронштейнов закреплен неподвижный диск 3 . В центре диска установлен вал 4 , проходящий через бункер. На валу жестко закреплена активная часть дозирующего органа – скребок 5 , выполненный в виде спирали Архимеда. К нижней части цилиндра прикреплен собирающий конус 6 , из него сыпучий материал может поступать на транспортер 7 или сменную емкость (не показано). Для предотвращения зависания материала и разрушения сводов в бункере на валу установлена ворошилка 8 . Привод спирали

V estnik of Omsk SAU, 2025, no. 3 (59)

AGROENGINEERING

и ворошилки осущестляется от главного вала стенда «СТДА» через клиноремённую передачу и червячный редуктор.

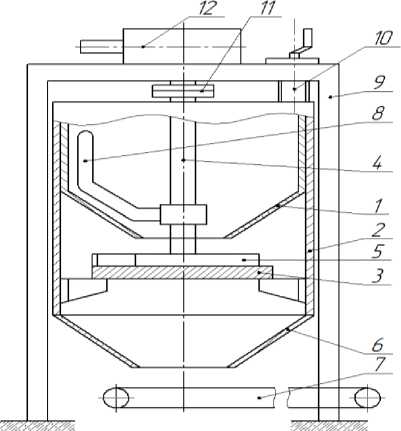
Рис. 1. Схема дозатора спирально-тарельчатого типа:

1 – бункер; 2 – цилиндр; 3 – диск; 4 – вал; 5 – скребок; 6 – конус; 7 – транспортер; 8 – ворошилка; 9 – рама; 10 – регулировочный винт; 11 – муфта; 12 – редуктор червячный

Были приняты следующие размеры: диаметр диска – 210 мм, шаг спирали – 40 мм, высота спирали – 20 мм. Количество витков спирали принято равным трем, высота загрузочного слоя на тарелке изменялась в пределах 22 – 47 мм с помощью подъемного механизма, перемещающего цилиндр. Частота вращения рабочего органа изменялась сменными шкивами и вариатором стенда в пределах от 5 до 25 мин^-1.

Работа предлагаемого дозатора: материал из бункера попадает в межвитковое пространство скребка, выполненного в виде спирали Архимеда. Вращаясь, спираль формирует материал в поток определенной формы и размеров и перемещает его к периферии неподвижного диска. Своей наружной поверхностью спираль непрерывно сбрасывает материал в кольцевую щель между цилиндром и диском. Производительность дозатора можно регулировать изменением частоты вращения спирали, высоты слоя материала на диске, а также диаметра выпускного отверстия бункера. На выгрузку значительно влияет то обстоятельство, что внешний слой материала на диске располагается под углом естественного откоса φ (рис. 2, а). При перемещении материала в зоне действия этого угла происходит интенсивное осыпание частиц, причем процесс осыпания непрерывен, пока вращается спираль. Высоту слоя перемещаемого материала с некоторыми допущениями можно принять равной величине зазора между диском и загрузочным цилиндром.

В зависимости от соотношения размеров диаметров загрузочного отверстия и тарелки, а также от числа рабочих витков спирали и ее высоты Н поперечное сечение слоя материала, сбрасываемого с диска, может иметь разную форму, а дозирующая установка – тот или иной режим работы. Наиболее часто встречается режим работы (рис. 2, б, позиция I) , при котором поперечное сечение слоя материала, сбрасываемого с диска последним рабочим витком спирали, состоит из прямоугольного участка и участка, представляющего прямоугольный треугольник с гипотенузой, расположенной под углом естественного угла φ к плоскости диска. В этом случае шаг спирали должен быть больше нижнего катета Н с сtg φ. В целом поперечное сечение

V estnik of Omsk SAU, 2025, no. 3 (59)

AGROENGINEERING

сбрасываемого слоя представляет неравнобокую трапецию Н с . Во втором случае (рис. 2, б, позиция II) , когда S ≤ Н с сtg φ, у поперечного сечения сбрасываемого материала форма прямоугольного треугольника .

На виде сверху показана кинематическая схема движения элементарного объема материала (точка А) под воздействием внешней стороны спирали по плоскости неподвижного диска. Точка А помещена в начале последнего витка спирали. При вращении спирали с частотой n и окружной скоростью v частица будет перемещаться по направлению v а . Воздействие спирали на материал с некоторыми допущениями можно представить, как действие плоской линейки, расположенной под углом α к направлению движения.

В связи с этим на рассматриваемом рисунке изображена развертка спирали длиной L, соответствующей последнему сбрасывающему витку. Линия развертки расположена под углом α к касательной к внутренней окружности. Развертка спирали проходит между линиями разверток наружной окружности диска радиусом R d и внутренней окружности радиусом R d – L .

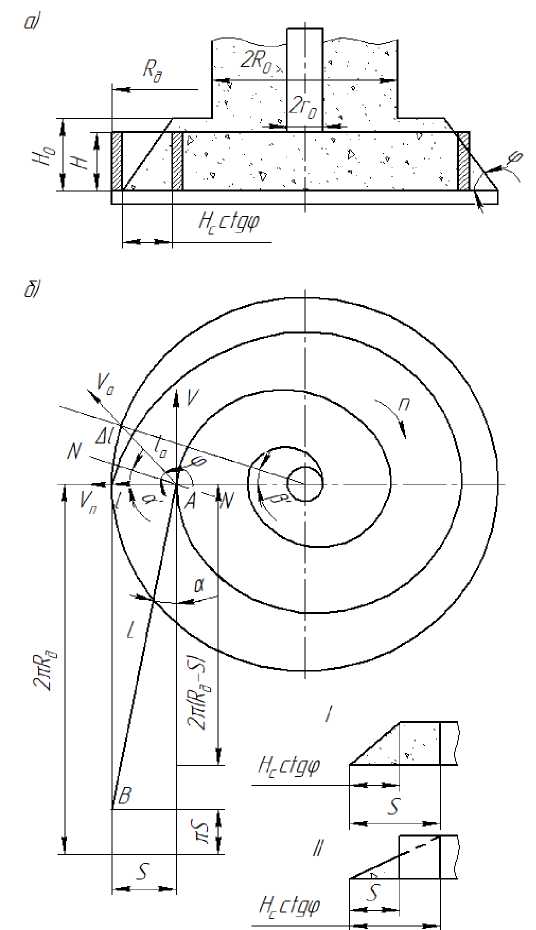
Рис. 2. Расчетная схема дозатора: а – вид сбоку; б – вид сверху

V estnik of Omsk SAU, 2025, no. 3 (59)

AGROENGINEERING

Длина развертки одного витка спирали определится по выражению

L 1 = S² + π²(2 R d – S )².                                     (1)

Общую длину многовитковой спирали можно определить по формуле

L= Lβ²/4 π ,                                        (2)

где β – величина угла вращения радиуса-вектора спирали, рад.

Согласно теории академика В.А. Желиговского [9] тело под воздействием косо поставленной линейки, движущейся по направлению v , будет перемещаться под углом трения φ¹ к нормали N или под углом α+ φ¹ к радиусу диска. Здесь φ¹ – угол трения материала о плоскость линейки (спирали). Сопротивление силы трения материала о поверхность диска не влияет на направление движения частицы. Таким образом, частицы материала совершают движение не в радиальном направлении со скоростью v n , а увлекаются спиралью в сторону ее вращения. В результате вектор скорости частиц отклоняется от радиуса на угол α + φ¹ . Поэтому за один оборот спирали частица переместится не на величину шага S со скоростью v n , а на величину L а со скоростью v а , причем частица не дойдет до внешней кромки диска на расстояние ∆ L . Пройденный частицей путь описывается выражением:

Lа= ( Rd – ∆ L)sin β1 / sin(α+ φ1),(3)

где β¹ – угол радиуса-вектора.

Значение радиальной скорости, выраженной через шаг и частоту вращения спирали, определится из выражения vn = Sn / 60.(4)

Фактическая скорость движения единицы массы материала будет иметь вид vа = Sn (1 – β1/2 π) / 60.(5)

Коэффициент радиального отставания массы материала рассчитаем по формуле

Ѱа = ∆ S100/ S= β1100/2 π,%.(6)

Одним из основных показателей, характеризующих работу дозатора, является его производительность. Общий вид формулы производительности дозатора зависит от режима его работы: первого ( I ) или второго ( II ). Сделаем вывод формулы производительности для более общего первого режима работы применительно к расчетной схеме дозатора, помещенной на рис. 2.

Напишем формулу производительности в общем виде:

Q = 60VnѰγ, кг/ч,                               (7)

где V – объем продукта, сбрасываемого скребком за один оборот, м3;

• n – частота вращения скребка, мин^-1;

• Ѱ – коэффициент снижения производительности;

• γ – объемная масса продукта, кг/ м³.

Коэффициент Ѱ учитывает снижение производительности дозатора под влиянием различных факторов. Выражение для этого коэффициента можно представить как произведение частных коэффициентов:

Ѱ = Ѱ 1 Ѱ 2 Ѱ 3 ,                                   (8)

где Ѱ 1 – коэффициент, учитывающий степень заполнения межвиткового пространства;

• Ѱ 2 – коэффициент, учитывающий радиальное отставание материала;

• Ѱ 3 – коэффициент, учитывающий объем спирали.

Дальнейший вывод формулы производительности дозатора сводится к определению объема материала, сбрасываемого за один оборот рабочего органа.

Применительно к первому режиму сбрасываемый объем можно представить как

V = V ус – V ц ,                                      (9)

где V ус – общий объем материала на диске (усеченный конус);

V estnik of Omsk SAU, 2025, no. 3 (59)

AGROENGINEERING

V ц – объем материала, оставшегося на диске (объем цилиндра).

Исходя из обозначений на расчетной схеме, эти объемы определятся по известным формулам [10]:

V ус = π Н с [( R d ² + R d (π Н с – Н с сtg φ) +( R d – Н с сtg φ)² ]/3 =

= π Н с ( R d ² – R d Н с сtg φ + Н с ² сtg² φ/3;

V ц = π Н с ( R d – S)² ;

V = π Нс (2 Rd S +( Нс2 сtg2 φ/3 – S2 – Rd Нс сtg φ).(10)

Подставляя значение V в выражение (7), получим формулу производительности в общем виде:

Qо = 60 π nѰγ Нс (2 Rd S +( Нс2 сtg2 φ/3 – S2 – Rd Нс сtg φ).(11)

Для частного случая режим работы дозатора, когда S= Н с сtg φ, формула имеет такой вид :

Q1= 60 π nѰγ Нс S(Rd – 2 S/3).(12)

По полученной формуле (11) рассчитана производительность рассматриваемого дозатора при работе на травяной муке (γ = 250 кг/м³). Частота вращения спирали была принята постоянной (n = 5 мин^-1). В качестве переменного аргумента взята высота слоя материала на тарелке Н с , которая изменялась от 22 до 47 мм с шагом ∆ Н с = 5 мм.

Расчетная производительность для указанного диапазона высоты слоя изменялась от 20 до 25 кг/ч, фактическая выдача находилась в пределах 18–27 кг/ч, причем при средних значениях высот отклонение фактической выдачи от расчетной было наименьшим.

Выводы

Предложен дозатор тарельчато-спирального типа для дозирования ингредиентов в линиях приготовления комбикормов, соответствующий зоотехническим требованиям по точности дозирования.

Представлена расчетная схема дозатора тарельчато-спирального типа и формула для определения производительности в общем виде.

Результаты экспериментальных исследований показали, что при средних значениях высот слоя материала отклонение фактической выдачи от расчетной было наименьшим.