Классификация монолитных конструкций по степени массивности

В теории зимнего бетонирования важнейшую

роль играет такой параметр, как массивность конструкции. Общеизвестно, что он характеризуется модулем поверхности1, в общем случае численно

равным отношению суммы площадей охлаждаемых поверхностей конструкции к ее объему:

М п

охл

V

Однако так было не всегда: на определенном этапе развития теории зимнего бетонирования использовалось обратная зависимость – отношение объема конструкции к площади поверхности [1].

Для упрощения расчетов для некоторых типовых конструкций определены формулы с учетом геометрии конструкций [2, 3], например:

– для плит и стен толщиной а , м:

М п

2 a ^,

– для колонн и балок квадратного сечения со стороной а , м:

М п

4 a ^,

– для кубов со стороной а , м:

М п

6 a

Продемонстрировать влияние данного параметра на технологические процессы зимнего бетонирования можно следующим образом:

– из первой теоремы Кондратьева [4] темп охлаждения конструкции пропорционален площади ее боковой поверхности и обратно пропорционален объему:

a F

m = v—-; cy V

– градиент температуры для объемной фигуры как величину, демонстрирующую равномерность распределения температуры по объему конструкции, можно записать в виде объемной производной:

j tdF grad (t) = lim F----.

v ^ o V

1 Интересно, что кроме того, что массивность характеризуется модулем поверхности, никакого определения термина массивности нет.

Таким образом, видно, что параметр массивности однозначно определяет температурные режимы выдерживания бетона. Однако для того чтобы выполнить в конкретных климатических условиях максимально достоверную предварительную оценку поведения выдерживаемых конструкций и назначить необходимые технологические параметры зимнего бетонирования, нужно иметь правильную классификацию конструкций по степени массивности.

Среди нормативной документации спорная классификация приведена в [5], согласно ей массивными конструкциями считают те, у которых минимальный геометрический размер составляет 0,8 м и более. То есть здесь для любых конструкций массивность определяется только одним геометрическим размером, что верно лишь для пластин и квадратных колонн. Более того, даже для пластин считать немассивной конструкцию толщиной 0,7 м, у которой Мп = 2,9 м^–1, представляется нелогичным.

Не менее спорное определение массивной конструкции приведено в [6]: массивной является та конструкция, для которой отношение площади поверхности, открытой для ее высыхания, к ее объему равно или меньше 2. То есть здесь рассматриваются не охлаждаемые поверхности (к которым относятся как открытые, так и утепленные поверхности, и поверхности, соприкасающиеся с негреющей опалубкой или с холодным грунтом), а только открытые поверхности. Такой подход к оценке массивности противоречит самой сути данного параметра в теории зимнего бетонирования, связанного с изменением температуры тела.

В научной и технической литературе представлено большое разнообразие мнений о классификации конструкции по степени массивности. Так, в [7] показано, что массивными являются конструкции с модулем поверхности до 4, а маломассивными – более 8. В [8] автор пишет: «…конструкция считается массивной при Мп < 6 м^–1, средней массивности – при Мп = 6…9 м^–1 и ажурной – при Мп > 9м^–1», видимо, под термином «ажурная» понимая «маломассивная» или «немассивная».

В монографии [9] предлагается считать: массивными – конструкции с Мп до 3 м^–1, средней массивности – с Мп 3…8 м^–1, немассивными – с Мп 8…12 м^–1. Таким образом, из классификации исчезает целый ряд конструкций с модулем поверхности более 12 м^–1.

В монографии [10] конструкции делятся на массивные с Мп до 6 м^-1 и маломассивные, к которым относят конструкции с Мп = 12^20 м^-1, а также стыки с Мп = 20.. .100 м^-1.

В работе [11] сказано, что среднемассивными являются конструкции с модулем поверхности 2– 12 м-1. Тогда очевидно, что массивными будут конструкции с модулем поверхности до 2 м-1, а немассивными - более 12 м-1.

Из продемонстрированного выше видно, что однозначной классификации конструкций, возводимых в зимних условиях, по степени массивности нет.

В качестве причины отсутствия однозначной классификации можно принять мнение о том, что «при одном и том же Мп , но разной конфигурации конструкции остывание происходит неодинаково» [12]. Об этом же указано в [13], где приведены аналитические зависимости для оценки модуля поверхности четырех групп конструкций.

Одной из последних работ, в которых рассмотрен вопрос классификации монолитных конструкций по степени массивности, является [14]. Авторы не предлагают своей классификации, а задаются вопросом о несовершенстве текущих классификаций и считают, что при оценке массивности необходимо учитывать не только геометрию конструкции, но и особенности как климатических условий, так и условий производства работ.

Более того, в [2] указано, что «любая конструкция может рассматриваться или как немассивная, или как массивная», и приводятся условия отнесения плит и колонн к немассивным конст- рукциям:

- для колонн:

А

Х< 2,

- для плит толщиной b :

А ■ b

---<

X

2,

где А - общий коэффициент теплообмена, Вт/ ° С; X - коэффициент теплопроводности материала, Вт/м ^° С.

Таким образом, перед нами стоит цель - разработать достоверную классификацию монолитных конструкций, выдерживаемых в зимних условиях, по критерию массивности.

Методика проведения исследования

Необходимо учесть, что параметр массивности имеет природное происхождение. Так, в 1847 году сформулировано правило Бергмана [15]: среди сходных форм теплокровных животных наиболее крупными являются те, которые живут в условиях более холодного климата. Это правило основано на предположении, что тепловыделение тела зависит от его объема, а скорость теплоотдачи - от площади его поверхности. При увеличении разме ров животных объем тела растет быстрее, чем его поверхность.

В дополнение к этому правилу можно привести и правило Аллена (1887 год). Согласно этому правилу среди родственных форм теплокровных животных, ведущих сходный образ жизни, те, которые обитают в более холодном климате, имеют относительно меньшие выступающие части тела: уши, конечности, хвосты и т. д. Сокращение размеров выступающих частей тела приводит к уменьшению площади поверхности тела и способствует экономии тепла. Видно, что природа создала гармонию между тепловыделением тела и его теплоотдачей, найдя оптимальное сочетание объема и площади поверхности тела.

Примем за истину наличие трех степеней (уровней) массивности конструкции - массивная, среднемассивная и немассивная. В данной работе был использован нестандартный подход к делению линейки значений массивности на отрезки (уровни). В основу этого подхода легла концепция золотого сечения [16] как математической категории, широко представленной в природе. Гармония золотого сечения тесно связана с гармонией природы, описанием которой занимается физика (в нашем случае раздел термодинамики [17]) путем применения необходимого для этого математического аппарата. Поэтому такой подход следует признать обоснованным. Более того, пропорции золотого сечения используются не только в искусстве и архитектуре, но и в целом ряде областей, далеких от них, например, в металлургии, в экономике и других [18-20].

Согласно [16] значение величины золотой пропорции d равно 1,618. На рис. 1 показано деление отрезка длиной в две единицы на три пропорциональных отрезка (в соответствии с тремя уровнями массивности). При этом образующийся ряд чисел при делении отрезка представляет собой геометрическую прогрессию и обладает аддитивными свойствами, присущими арифметическому ряду: 1, 1/ d , (1/ d)².

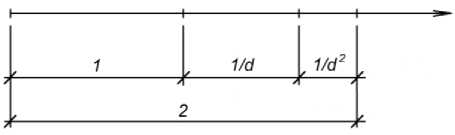
Рис. 1. Деление отрезка длиной 2 единицы согласно концепции золотого сечения

Учитывая, как было показано выше, что массивность влияет на равномерность распределения температуры по объему конструкции, из первой теоремы Кондратьева видно, что за такую равномерность отвечает и параметр у - коэффициент неравномерности распределения температуры в теле конструкции. Этот коэффициент принимает значения от стремящегося к 0 (температуры по объему тела распределены абсолютно неравномерно - т. е. конструкция массивна), до 1 (температуры по объему одинаковы - т. е. конструкция немассивна). Следовательно, между Мп и у можно установить прямую взаимосвязь, а деление массивности на уровни определить через коэффициент у по пропорции золотого сечения.

Результаты исследования

Преобразуем рис. 1 с учетом того, что шкалой значений будет являться коэффициент неравномерности у , значения которого лежат в диапазоне (0;1] (рис. 2). Тогда получим, что массивным конструкциям будет соответствовать диапазон коэффициента у от 0 до 0,5, среднемассивным - от 0,5 до 0,809, немассивным – от 0,809 до 1. Причем эти диапазоны будут постоянны для любых конструкций, независимо от их формы и размеров.

Исследуем взаимосвязь модуля поверхности с коэффициентом неравномерности распределения температур для ряда конструкций, чей модуль поверхности определен во введении к данной статье. Из [4]:

у = (B2 +1,44B +1)-0,5, где В – модифицированная форма числа Bi.

a FK а К

B =     =    М_п ,

X V    X п здесь а - коэффициент теплоотдачи (принят в дальнейшем 6,3 Вт/(м2-°С)); X - коэффициент теплопередачи бетона (принят 2,6 Вт/(м-°С)); К -коэффициент формы тела (м2):

К =

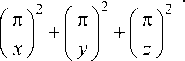
Запишем результаты расчетов для кубов в табл. 1, а зависимость коэффициента неравно- мерности распределения температур в теле конструкции от модуля ее поверхности представим в виде графика (рис. 3).

Видно, что для монолитных конструкций, имеющих форму куба, массивными следует считать конструкции с модулем поверхности до 2,57 м–1, среднемассивными – с модулем поверхности от 2,57 до 9,78 м–1, а немассивными – с модулем поверхности более 9,78 м–1.

Построим аналогичные графики для колонн и балок квадратного сечения (рис. 4) и для плит и стен (рис. 5).

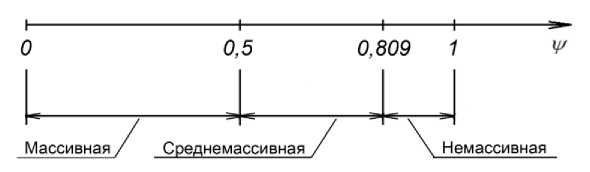
Рис. 2. Деление коэффициента неравномерности распределения температур по степени массивности конструкций

Таблица 1

Расчетные параметры для кубов

Размер ребра, а , м	Модуль поверхности, Мп , м–1	Коэффициент формы, К	Модифицированная форма числа Bi	Коэффициент неравномерности распределения температур, у
0,15	40,00	0,00076	0,0738	0,948
0,2	30,00	0,00135	0,0985	0,932
0,3	20,00	0,00304	0,1477	0,900
0,4	15,00	0,00541	0,1969	0,870
0,5	12,00	0,00845	0,2462	0,841
0,6	10,00	0,01217	0,2954	0,813
0,7	8,57	0,01657	0,3446	0,787
0,8	7,50	0,02164	0,3939	0,762
0,9	6,67	0,02738	0,4431	0,738
1,0	6,00	0,03381	0,4923	0,716
1,5	4,00	0,07607	0,7385	0,619
2,0	3,00	0,13523	0,9847	0,543
2,5	2,40	0,21130	1,2309	0,483
3,0	2,00	0,30427	1,4770	0,434
3,5	1,71	0,41415	1,7232	0,394
4,0	1,50	0,54093	1,9694	0,360
6,0	1,00	1,21709	2,9541	0,267

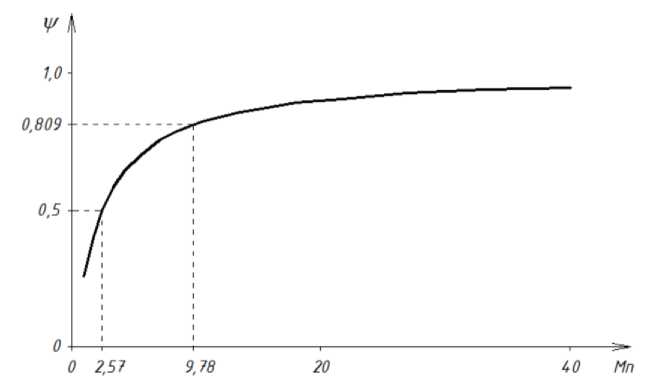
Рис. 3. Взаимосвязь коэффициента неравномерности температур и модуля поверхности для конструкций типа куб

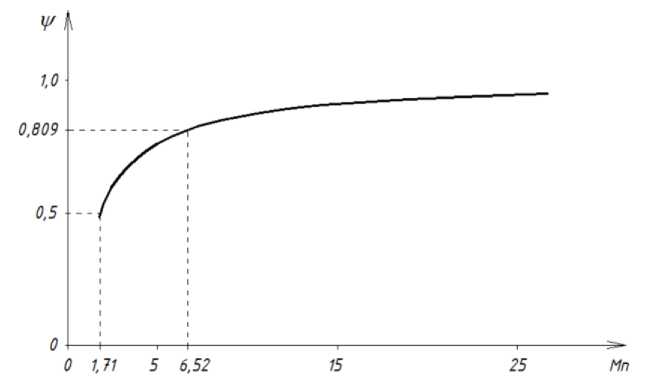
Рис. 4. Взаимосвязь коэффициента неравномерности температур и модуля поверхности для колонн и балок квадратного сечения

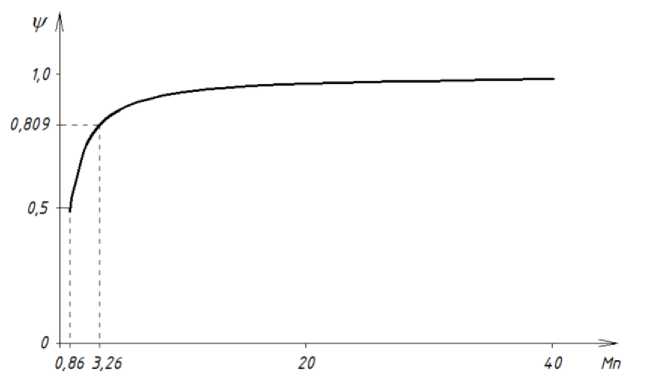
Рис. 5. Взаимосвязь коэффициента неравномерности температур и модуля поверхности для плит и стен

Таблица 2

Классификация монолитных конструкций по степени массивности

Конструкция	Модуль поверхности конструкции, м–1, для степени массивности
	Массивная	Среднемассивная	Немассивная
Куб	менее 2,57	2,57…9,78	более 9,78
Колонна, балка	—	менее 6,52	более 6,52
Плита, стена	—	менее 3,26	более 3,26