Классификация относительно регулярных алгебр

Регулярные языки являются одним из основных объектов теории формальных языков. Особый интерес вызывает задача проверки некоторого регулярного условия для слов фиксированного языка. Рассмотрим некоторый язык L. Входом задачи регулярной реализуемости является регулярный язык R, заданный, например, некоторым автоматом. Необходимо проверить непустоту пересечения L и R. Подробное рассмотрение задач регулярной реализуемости приводится в работах [2] и [8]. В [2] и [3] приводятся примеры языков, задачи регулярной реализуемости для которых полны в хорошо изученных сложностных классах.

В данной работе рассматривается обобщение задачи регулярной реализуемости. Основным инструментом является понятие относительно регулярных булевых алгебр. По произвольному языку строится булева алгебра, состоящая из всех возможных его пересечений с регулярными языками. Существует гомоморфизм из алгебры регулярных языков REG на относительно регулярную алгебру языка L, задаваемый следующим образом: <Дх) = х О L. Таким образом, соответствующую задачу регулярной реализуемости можно перефразировать: является ли образ регулярного языка при заданном выше гомоморфизме не нулём?

Основным результатом работы является теорема о совпадении классов атомных булевых алгебр и относительно регулярных алгебр.

(с) Шимапогов И. Н., Вялый М.Н., 2024

@ Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (национальный исследовательский университет)», 2024

2.    Булевы алгебры

В данном разделе определения и основные результаты даются в соответствии с [1].

Определение 1. Булевой алгеброй называется множество М с бинарными алгебраическими операциями V и Л, а также унарной алгебраической операцией —, такими что Va, b, c Е М:

• 1)    a V b = b V a'

• 2)    a V (b V c) = (a V b) V c.

• 3)    a V a = a'

• 4)    a V (b Л c) = (a V b) Л (a V c).

• o) —(a V b) = —a Л —b'.

• 6) (a Л —a) V b = b:

• i)    ——a = a.

На произвольной булевой алгебре можно ввести отношение частичного порядка: a С b ^^ a Л b = a. Минимальный ii макснмальиый элемент обозначим как 0 н 1 соответственно. Нетрудно проверить, что в булевой алгебре такие элементы уникальны и обладают свойствами a V 0 = a = a Л 1, a Л 0 = 0 и a V 1 = 1. Особый интерес при изучении булевых алгебр играют атомы.

Определение 2. Будем называть ненулевой элемент a атомом, если верно следующее:

b С a ^ (b = 0) inn (b = a).

Определение 3. Алгебру А будем называть атомной, если Va Е А Ab Е А b С a и b — атом.

Как и для других алгебраических структур, важным оказывается понятие идеала булевой алгебры и его связь с гомоморфизмами.

Определение 4. Пусть А — булева алгебра, а I С А. I называется идеалом, если I содержит 0. для каждого элемента i из I все меньшие i элементы также содержатся i I i I замкнуто относительно операции V.

Отдельно подчеркнём, что идеал булевой алгебры сам может не являться булевой алгеброй. Идеал индуцирует соотношение эквивалентности на булевой алгебре (х ~i у ^^ (х Л —У) V (у Л —х) Е Г), факторизация по которому снова дает булеву алгебру.

Определение 5. Гомоморфизмом булевой алгебры А в булеву алгебру В называется отображение р. такое что p(a V b) = p(a) V p(b). p(a Л b) = p(a) Л p(b). p(—a) = —(p(a)).

Теорема 1 (см. [1]).   1) Рассмотрим гомоморфизм р из булевой алгебры А. Тогда его ядро является идеалом данной алгебры и р(А) изоморфно А/Керр).

• 2)    Пусть I — это идеал булевой алгебры А. Тогда суирствует гомоморфизм p(a) = a/I. такой что р(А) изоморфно А/Керр).

Наиболее важным для данный работы является идеал Фреше.

Определение 6. Идеалом Фреше F (А) булевой алгебры А называется идеал, состоящий из всех конечных дизъюнкций её атомов.

Помимо идеала оказывается полезным двойственное понятие фильтра.

Определение 7. Пусть А — булева алгебра, a F С A. F называется фильтром, если F содержит 1. для каждого элемента f из F все большие f элементы также содержатся в F я F 'замкнуто отпоентслыю операции Л.

Определение 8. Если фильтр F С А таков, что для каждого a G А выполняется a G F или —a G F, то он называется ультрафильтром.

Далее мы будем иметь дело только со счётными булевыми алгебрами.

Определение 9. Булева алгебра называется счётной, если её мощность счётна.

В случае счётных булевых алгебр оказывается верна следующая важная лемма.

Лемма 1 (см. [1]). Пусть А и В — это счётные атомные булевы алгебры и их факторы по идеалам Фреше изоморфны, тогда и сами эти алгебры изоморфны.

3.    Двойственность Стоуна. Пространства Стоуна как деревья

Широко известна двойственность Стоуна для булевых алгебр. Подробное её рассмотрение приводится, например, в [4].

Определение 10. Будем называть топологическое пространство X стоуновским, если оно:

• 1)    компактно;

• 2)    хаусдорфово;

• 3)    множество всех открыто-замкнутых множеств B(X ) является базой топологии.

Теорема 2 (см. [4]).   1) Для каждой булевой алгебры А существует стоуновское про странство Sa, такое, что А изоморфно B(Sa) с теоретико-множественными операциями.

• 2)    Для каждого стоуновского пространства X существует булева алгебра А такая, что А изоморфно В(X ) с теоретико-множественными операциями.

Отметим, что точки в Sa соответствуют ультрафильтрам булевой алгебры А. При этом атомы алгебры соответствуют открыто-замкнутым множествам, состоящим из одной изолированной точки. Будем называть Sa пространством Стоуна алгебры А.

Сформулируем некоторый набор важных следствий двойственности Стоуна:

Лемма 2 (см. [4]). Булева алгебра счётна ж^ её пространство Стоуна метризуемо.

Лемма 3 (см. [4]). Булева алгебра атомна ж^ её пространство Стоуна содержит всюду плотное множество изолированных точек.

Лемма 4 (см. [4]). Булевы алгебры изоморфны ж^ их пространства Стоуна гомео-морфны.

Лемма 5 (см. [4]). Рассмотрим две булевы алгебры А и В. В является гомоморфным образом А ж^ Sb гомеоморфно подпространству Sa-

Определение 11. Для произвольного топологического пространства X назовем производной Кантора - Бендиксона X ‘ подпространство, состоящее из неизолированных точек.

Лемма 6 (см. [5]). Если В изоморфно А/F(А), то Sb гомеоморфно S'_a.

На ультрафильтры счётной булевой алгебры естественно смотреть как на гомоморфизмы из нее в алгебру из двух элементов. Рассмотрим произвольную счетную булеву алгебру, зафиксируем некоторую нумерацию её элементов. Тогда каждому гомоморфизму соответствует бесконечное двоичное слово (сверхслово), в котором на п-месте стоит 0, если гомоморфизм отображает п-й элемент алгебры в 0, и 1 в противном случае. Множество таких слов представляется как корневое дерево, вершины которого — это префиксы этих сверхслов. Получаем, что пространство всех ультрафильтров этой булевой алгебры можно представить как бесконечное корневое дерево, где каждая вершина имеет одного или двух потомков. Далее для каждой булевой алгебры будем рассматривать соответствующее ей пространство Стоуна как бинарное дерево описаной выше конструкции. Отметим, что ветвь дерева (сверхслово) — это и есть точка в пространстве Стоуна, а множество всех ветвей с общим префиксом образует открыто-замкнутое множество.

Так как дальнейшее рассмотрение будет касаться лишь атомных булевых алгебр, то определим, какие деревья соответствуют им, и выделим основные их свойства.

Определение 12. Будем называть ветвь дерева изолированной, если данная ветвь состоит из вершин с одним потомком, начиная с некоторого места.

Определение 13. Будем называть множество ветвей дерева всюду плотным, если любая вершина является префиксом ветви из этого множества.

Из леммы 3 вытекают следующие утверждения.

Лемма 7. Счётные атомные булевы алгебры соответствуют деревьям, в которых есть всюду плотное изолированное множество ветвей.

Лемма 8. Безатомной счётной булевой алгебре соответствует полное бинарное дерево.

Заметим, что гомеоморфизм рассматриваемых деревьев в данном случае равносилен гомеоморфизму стоуновских пространств. Также из лемм 1, 4 и б следует критерий гомеоморфизма деревьев.

Лемма 9. Два дерева, соответствующих пространствам Стоуна, гомеоморфны ^^ геомеоморфны деревья, получаемые из исходных удалением изолированных ветвей.

4.    Алгебры языков. Относительно регулярные алгебры

Так как регулярные языки замкнуты относительно объединения, пересечения и дополнения, то они образуют булеву алгебру REG. Соответствующее им пространство Стоуна принято называть пространством профинитных слов. Подробное рассмотрение свойств данного пространства приводится в [6].

Лемма 10 (см. [7]). Фактор REG по идеалу Фреше является безатомной алгеброй.

Определение 14. Рассмотрим произвольный язык L. Будем называть относительно регулярной алгеброй для L булеву алгебру REG г = {М С L | М G REG} с операциями объединения, пересечения и дополнения до L.

Заметим, что REG 3* совпадает с REG. Из определения также видно, что относительно регулярная алгебра всегда является гомоморфным образом алгебры регулярных языков, соответствующий гомоморфизм имеет вид р(х) = х П L. Стоит отметить, что относительно регулярные алгебры всегда атомны — в роли атомов в них выступают языки из одного слова. Докажем также следующую лемму.

Лемма 11. Пусть L — это некоторое множество слов. Рассмотрим его как подмножество Sreg- Тогда замыкание L гомеоморфно Sreg_l-

Воспользуемся следующим фактом: пересечение элементов базы топологии с подпространством является базой топологии этого подпространства. По теореме 2 регулярные языки являются базой топологии Skeg- Рассмотрим произвольный регулярный язык R как подмножество Skeg- Тогда R И L = R И L. (Здесь L — это замыкание множества L в топологическом пространстве Sreg) Следовательно, языки вида R И L являются базой топологии пространства L, а значит, L гомеоморфно Sreg_L'

5.    Основные результаты

Сформулируем и докажем основной результат данной работы.

Теорема 3. Для любой атомной алгебры существует изоморфная ей относительно регулярная алгебра.

Пусть Т — дерево, полученное из полного бинарного следующей процедурой: разобьем каждое ребро на два и из новой вершины выпустим бесконечную ветвь. Оно имеет следующий вид:

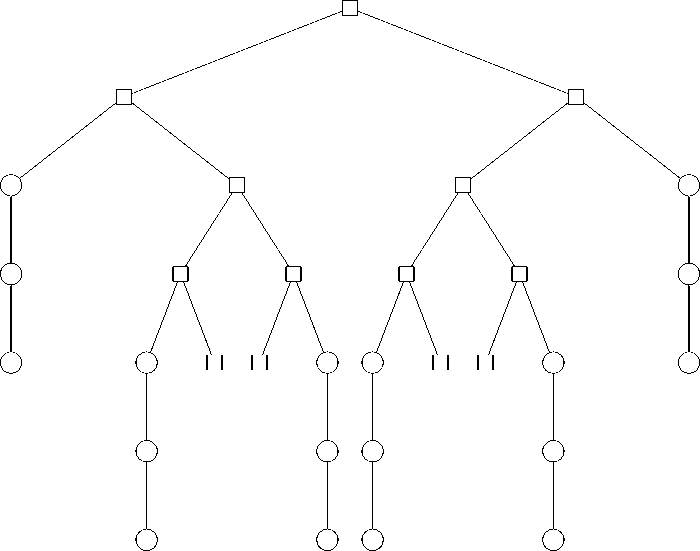
Определение 15. Будем называть вершину неветвящейся, если она входит в одну ветвь. (Эквивалентно, у нее и у всех её потомков ровно по одному потомку.)

Круглыми вершинами на рисунке помечены неветвящиеся вершины. Заметим, что после удаления всех изолированных ветвей данное дерево превращается в дерево, гомеоморфное полному бинарному, а, значит, оно соответствует алгебре, изоморфной REG по леммам 8, 9 и 10.

Рассмотрим произвольную атомную алгебру R, ей соответствует некоторое дерево Tr. Вложим его в дерево Т таким образом, чтобы прообраз любой изолированной ветви был изолированной ветвью. Для начала заметим, что если образ некоторой вершины — невет-вящаяся вершина, то образ её потомков определяется однозначно.

Определение 16. Будем называть уровнем п дерева множество всех вершин, которым соответствует слово длины п.

Сопоставим корню дерева Tr корень дерева Т. Пусть мы вложили в Т вершины дерева Tr уровня не больше п. Причём образ каждой ветвящейся вершины имеет двух ветвящихся потомков, а образ каждой неветвящейся вершины — неветвящаяся вершина. Рассмотрим

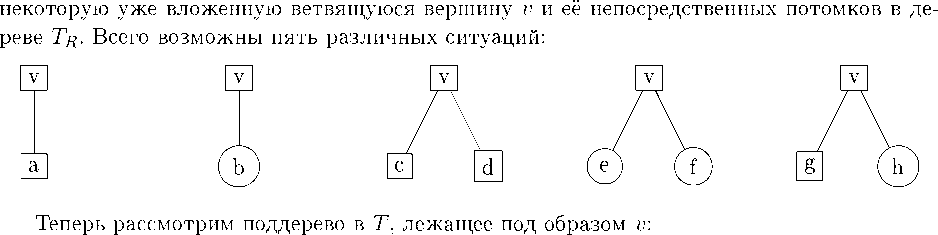
Заметим, что образ потомков можно определить, сохраняя заданные свойства. Для приведенных пяти случаев в качестве образов выберем вершины по правилу:

^(о) = 2,

= 1, р⁽с) = 2, p⁽d) = 3, ^(е) = 1, p-J ) = ⁴, ^д) = ², v(^) = 4.

Таким образом, мы построили поддерево в Т, гомеоморфное дереву Tr со следующим свойством: прообраз любой изолированной ветви является изолированной ветвью. Эквивалентно, мы выделили в пространстве Sreg подпространство X, такое что любая изолированная точка в X является изолированной и в Sreg- Назовем множество всех таких точек L. Тогда, по лемме 11, исходная алгебра R изоморфна относительно регулярной алгебре для данного L.