Компетентностный подход в организации самостоятельной работы студентов при изучении математических дисциплин

Модернизация российского образования сегодня, связанная с приближением к общеевропейским и мировым стандартам, глобализацией рынка труда, переходом к личностной парадигме и ориентацией на конечный результат, вызывает пересмотр целевых установок, содержания, принципов и методов подготовки специалистов и бакалавров.

При этом математическое образование было и остается одной из основ профессионального образования специалиста любого профиля, особенно технического и экономического. Вузовский курс высшей математики, являясь естественнонаучной дисциплиной, составляет базу фундаментальной подготовки студентов, обеспечивает формирование целостного математического подхода к анализу объектов и процессов во всех областях научного знания специалистов. В ходе математической подготовки студенты должны получить представление о математике как особом способе познания мира, об общности ее понятий и представлений; развить логическое и алгоритмическое мышление; овладеть основными методами исследования и решения математических задач теоретического и практического характера, необходимыми для изучения общенаучных и специальных дисциплин; выработать умения самостоятельно расширять математические знания и проводить математический анализ прикладных задач. В процессе изучения математики необходимо воспитать у студентов высокую математическую культуру, достаточную для применения математического аппарата в будущей трудовой деятельности; сформировать умения автоматизации математических вычислений (численных, символьных, графических) при помощи современных компьютерных математических систем; научить строить математические модели различных технологических процессов, строить матрицы планирования и проводить эксперимент в соответствии с ними строить адекватные линейные и нелинейные модели, принимать решения после построения модели. Таким образом, основным итогом изучения математики сегодня должны выступать не только математические знания как таковые, но и способность актуализировать их непосредственно в трудовой деятельности, при рассмотрении конкретных профессиональных проблем, а также приобретать новые математические знания, используя современные образовательные и информационные технологии.

Методология

Решение поставленных задач требует компетентностного подхода в организации деятельности студентов в процессе профессионального образования вообще и в математической подготовке в частности, так как он подразумевает формирование знаний, умений, опыта и отношений, объединенных в единое целое. Конечной целью вузовского образования в современном мире становится именно освоение компетенций, а сами компетенции оказываются результатами обучения. Отметим также, что интегративность компетентностного подхода в обучении проявляется не только в целостности знаний, умений и опыта, но и в формировании личностных качеств студентов, положительно влияющих на эффективность труда и конкурентоспособность специалиста.

Практико-ориентированное образование, во-первых, подразумевает сочетание фундаментального образования и профессионально-прикладной подготовки, во-вторых, имеет в основе своей деятельностный характер. Компетенции и деятельность неразрывно связаны: компетенции формируются в процессе деятельности студента и ради его будущей профессиональной деятельности. Поскольку главным смыслом компетентностного подхода является способность к самостоятельной профессиональной деятельности, то именно самостоятельная работа студентов лежит в основе его реализации. Более того, некоторые исследователи вопроса выделяют самостоятельно-деятельностную компетентность как отдельную единицу [1].

Несмотря на значительное число исследований по реализации компетентно-стного подхода в организации самостоятельной работы студентов, следует отметить, что имеет место недостаточная разработанность дидактических аспектов использо- вания данного подхода в ходе изучения математических дисциплин, а также ”нетех-нологичность” имеющихся разработок. По нашему мнению, это следует считать главными причинами разрыва между потенциальными и реальными возможностями использования компетентностного подхода в современном профессиональном образовании. Таким образом, существует противоречие между объективной необходимостью научно обоснованной организации компетентностного подхода и недостаточной разработанностью педагогических условий его эффективного использования в вузовской математической подготовке [2].

Одним из способов разрешения данного противоречия является выявление педагогических условий интенсификации учебно-воспитательного процесса – повышение эффективности и качества обучения, обеспечение мотивов познавательной деятельности, углубление межпредметных связей за счет интеграции информационной и предметной подготовки; совершенствование управления самостоятельной работой студентов на различных этапах математической подготовки.

Целостная природа компетенций требует целостности их освоения. Следовательно, стоит проблема нахождения технологий обучения, позволяющих объединять и сочетать изучение теории, получение практических навыков и приобретение некоторого опыта, связанного со спецификой выбранной профессии, и предполагающих активную деятельность самих студентов. Традиционное проведение только лекционных и практических занятий по математике не полностью решают этот вопрос: в первом случае на должном уровне не обеспечивается акцент на самостоятельную работу студентов, а во втором можно столкнуться с трудностями приобретения профессионального опыта в связи с ограниченностью применяемых средств обучения. Новые образовательные стандарты, направленные на саморазвитие, самоопределение и самореализацию студента, заставляют преподавателей иначе подходить к организации занятий, искать новые виды занятий или новое наполнение традиционных форм обучения.

Весьма уместным в контексте рассматриваемой проблемы может оказаться введение лабораторных работ по математике (в дополнение к лекциям и практикам). Актуальность занятий такого вида продиктована также повсеместной компьютеризацией различных сфер деятельности человека и, как следствие, наличием высокой степени готовности современных студентов к использованию ПЭВМ и компьютерных технологий в образовательном процессе. Это связано как со стремительным внедрением информационных технологий буквально во все сферы жизни, так и с тенденциями современного школьного образования. Молодежь очень быстро откликается на все новое и активно выражает готовность к применению информационных технологий, и прежде всего, в образовании. Первокурсники приходят в вуз уже вооруженные знаниями современных компьютерных технологий, умениями работать с электронными ресурсами. В связи с этим, сложности адаптирования к вузовскому курсу математики на лабораторных работах не возникает. На наш взгляд, лабораторные работы наиболее полно способствуют развитию самостоятельности мышления, структурированию и закреплению знаний, формируют навыки применения теоретических знаний в практической деятельности.

Реализация

В Юго-Западном государственном университете в рабочих учебных планах многих специальностей и направлений подготовки предусмотрены лабораторные работы по математике. Тенденции таковы, что лабораторные работы по математике сейчас проводятся не только на дневном отделении, но и на заочной и сокращенных формах обучения. Для успешной реализации поставленных задач требуются большие временные затраты на разработку учебно-методических пособий, проверку индиви- дуальных заданий и т. д. Однако опыт работы показывает, что подобный подход дает положительные результаты в плане повышения качества подготовки студентов.

Преподаватели кафедры высшей математики университета на протяжении последних лет довольно успешно используют компьютерные технологии. Выявляются этапы образовательного процесса, когда применение мультимедийных технологий наиболее целесообразно и дает существенный выигрыш по сравнению с традиционными формами обучения. К примеру, на кафедре разработана и прошла экспериментальную проверку компьютерная обучающая программа «Электронный учебник» по разделу курса «Теория вероятностей», студенты и преподаватели используют интер-нет-тренажеры для текущей и рубежных проверок знаний и т. д. В рамках настоящей статьи мы подробно остановимся на проведении лабораторной работы «Метод наименьших квадратов».

Метод наименьших квадратов (МНК) - один из наиболее часто используемых методов при обработке эмпирических данных, построении и анализе физических, биологических, технических, экономических и социальных моделей. С помощью МНК решают задачу выбора параметров функции (заранее заданного вида) для приближённого описания зависимости величины у от величины х . Исходные данные могут носить самый разнообразный характер и относиться к различным отраслям науки или техники, например: зависимость продолжительности службы электрических ламп ( у ) от поданного на них напряжения ( х ); зависимость предела прочности стали ( у ) от содержания углерода ( х ); зависимость цен товара ( у ) от спроса ( х ) на этот товар; зависимость температура воздуха ( у ) от высоты над уровнем моря ( х ) и другие зависимости.

Данная работа выполняется студентами почти всех специальностей второго курса. В начале занятия актуализируется необходимый теоретический материал, разбираются примеры. Затем студентам выдаются индивидуальные задания, представляющие собой данные о дискретной зависимости величины у от величины х , для решения задачи аппроксимации линейной и квадратичной функциями. В ходе выполнения лабораторной работы у преподавателя есть возможность проверить выполнение заданий каждым студентом. Контроль полученных знаний и умений осуществляется на следующем занятии в процессе защиты лабораторной работы, подразумевающей ответы на теоретические вопросы, выполнение небольших по объему тестовых заданий и решение практических задач на применение метода. Опыт показал, что некоторые предложенные на защите задачи вызывали у студентов затруднения, что свидетельствовало об их неспособности применять полученные теоретические знания к практике.

Появилась осознанная необходимость осуществить подбор таких заданий к лабораторным работам, выполнение которых способствовало бы формированию практического опыта. В результате были подготовлены индивидуальные задания практического содержания с учетом специфики выбранной специальности [3].

Приведем несколько примеров использованных заданий.

В группах, обучающихся по специальностям «Автомобили, автомобильное хозяйство», «Эксплуатация транспортных средств», «Сервис (автосервис)» и др. студентам были предложены следующие задания, подобные следующим:

1) В таблице приведены данные о расходе топлива ( у , л на 100 км) автомобиля с дизельным двигателем с механической трансмиссией в зависимости от скорости движения ( х , км/ч).

хi	10	20	40	60	90	110	120	130	140	150
у i	2,5	2,8	3	3,9	4,8	5,5	5,7	7	8,1	9,4

В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии y = kx + b . Спрогнозировать расход топлива при скорости 160 км/ч.

2) В таблице приведены данные о зависимости вырабатываемой резистором мощности Р (усл. ед.) от напряжения U (усл. ед.)

U i	10	30	60	80	100	120	140	160	180	200
P i	10	90,2	359	638	999,9	1438	1961	2562	3240	4001

В предположении, что между U и P существует квадратичная зависимость P = a 2 U ²+ a 1 U + a 0 , определить параметры регрессии. Спрогнозировать мощность при напряжении 170 .

Студентам строительных специальностей (профили «Промышленное и гражданское строительство», «Городское строительство и хозяйство», «Экспертиза и управление недвижимостью», «Водоснабжение и водоотведение» и др.) предлагались задания следующего плана:

1) В таблице приведены данные о зависимости теплопроводности легких бетонов ( у , Вт/(м∙ С^о) от плотности ( х , кг/м³).

хi	800	900	1000	1100	1200	1300	1400	1500	1600	1700
у i	0,2	0,22	0,24	0,28	0,33	0,38	0,4	0,42	0,44	0,47

Предполагая линейную зависимость у от х , определить параметры линейной регрессии y = kx + b . Получить прогноз теплопроводности при плотности 1800 кг/м³.

2) В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака. В таблице приведены данные об изменении высоты ( h , м) и времени ( t , мин).

ti	1	2	4	6	8	10	12	15	18	20
h i	3,6	3,2	2,57	1,95	1,45	1,09	0,9	0,6	0,3	0,1

В предположении, что между t и h существует квадратичная зависимость, определить параметры регрессии h = a 2 t ²+ a 1 t + a 0 . Спрогнозировать время, когда бак опустеет.

Студенты специальностей «Конструирование и технология электронных средств», «Информатика и вычислительная техника» (различные профили), «Программное обеспечение вычислительной техники и автоматизированных систем» получили задания, подобные следующим:

1) В таблице приведены результаты измерений сопротивления проводника ( R , Ом) в зависимости от температуры ( t, ⁰С).

t	100	200	300	400	500	600	700	800	900	1000
R	15	19	23	27	31	34	37	39	42	45

В предположении, что между t и R существует линейная зависимость, определить параметры линейной регрессии R = kt + b . Cделать вывод о возможном сопротивлении проводника при температуре 60⁰С.

2) В таблице приведены данные о времени работы ( t , у.е.) некоторого алгоритма в зависимости от количества его элементов ( x ).

хi	9	12	14	16	18	20	21	23	24	25
t i	152	280	380	500	630	780	860	1025	1130	1225

В предположении, что между х и у существует квадратичная зависимость, определить параметры регрессии y = a 2 x ²+ a 1 x+ a 0 . Спрогнозировать время работы алгоритма, состоящего из 30 элементов.

В группах экономических специальностей (профили «Бухгалтерский учет, анализ и аудит», «Финансы и кредит», «Налоги и налогообложение» и др.) предлагались задания, подобные следующим:

1) Показатели по объему производства ( х , у.е.) и затратам ( у , тыс. руб.), взятые из отчетной ведомости предприятия за 10 месяцев, приведены в таблице.

хi	4,25	4,3	4,4	4,42	4,45	4,5	4,53	4,55	4,6	4,62
у i	530	540	553	554	557	560	565	568	571	572

Полагая, что зависимость между х и у задается формулой y = kx + b , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b . Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е.

2) В таблице приведены данные о показателях конкуренции ( x ) и средневзвешенные по частоте упоминания количества патентов ( у ).

х i	0,87	0,88	0,89	0,9	0,91	0,92	0,93	0,94	0,95	0,96
у i	3,3	3,6	4,2	4,5	4,8	5,3	5,9	6,1	6,4	6,1

В предположении, что между х и у существует квадратичная зависимость, определить параметры регрессии y = a 2 x ²+ a 1 x+ a 0 . Спрогнозировать количество патентов, в случае, если показатель конкуренции равен 0,85.

Предположение о преимуществах компетентностного подхода в организации самостоятельной работы студентов в рассматриваемом случае и выявление условий его эффективности требовали серьезного анализа. В связи с этим, было принято решение организовать лабораторную работу на основе компетентностного подхода в половине учебных групп разных специальностей, а в другой половине оставить проведение лабораторных занятий в прежней форме.

Деятельность преподавателей по подготовке лабораторной работы не ограничивалась подбором заданий, а включала выбор средств для их выполнения и разработку четких методических указаний [3]. Компетентностный подход в организации работы определил выбор необходимого для решения задач программного продукта. Способность приобретать новые математические знания, используя современные информационные технологии, – суть одной из компетенций, подлежащих освоению. В связи с этим, студентам инженерных специальностей предлагалось выполнить работу, используя программный пакет Mathcad, а экономических – Excel, ведь в профессиональной деятельности экономисты часто сталкиваются с работой в Excel, а инженерным специальностям «ближе» Mathcad. Таким образом, студенты овладевают не только математическими знаниями, но и навыками работы с теми компьютерными средствами, которые нужны в будущем .

Методические указания, которые сопровождали работу, были сжатыми и краткими по содержанию, но при этом содержащими информацию, позволяющую изучить данный раздел курса в необходимом объеме. В процессе выполнения лабораторной работы студенты были обеспечены четкой и адекватной информацией о последовательности выполняемых действий, что поддерживало их уверенность в себе, стимулируя тем самым внутреннюю мотивацию. Формированию глубоких мотивов учения и успешности учебной работы способствовали спокойный и доброжелательный тон общения, оптимистический настрой преподавателя и студентов. В процессе проведения лабораторной были соблюдены следующие принципы: 1) принцип доступности, учета уровня подготовленности, индивидуальных возможностей обучающихся, соотнесенных с мерой трудности изучаемого; 2) принцип основательности и прочности усвоения ключевых элементов, логики, структуры изучаемой дисциплины, практических навыков и умений; 3) принцип создания положительного эмоционального климата, мотивационного обеспечения деятельности и системы отношений; 4) принцип рационального сочетания коллективных и индивидуальных форм и способов учебной работы, обеспечивающих развитие личности, ее индивидуальную самореализацию.

Анализ и оценка разработки

Анализ результатов работы осуществлялся по следующим критериям:

• V    степень сформированности у студентов математических знаний и умений;

• V    наличие мотивационно-потребностной сферы в плане использования компьютерных технологий обучения;

• V    степень сформированности рефлексивной позиции.

Вопрос о сформированности математических знаний и умений у студентов решался на основе результатов, полученных в экспериментальных и контрольных группах по одинаковым по сложности теоретическим вопросам и тестовым материалам, и приведенных в таблице №1.

Таблица №1

Уровень	Контрольные группы	Экспериментальные группы
Низкий	39,1%	38,2%
Средний	45,4%	45,7%
Высокий	15,5	16,1

На основании полученных данных можно констатировать незначительные различия в уровне математических знаний и умений в контрольных и экспериментальных группах.

Для получения качественного анализа психологических свойств и состояний студентов в контрольных и экспериментальных группах использовали опросник В.К. Гербачевского, предназначенный для выявления уровней притязаний испытуемых посредством диагностики компонентов мотивационной структуры личности. Мы выявили внутренний и познавательные мотивы, которые характеризовали студентов, как проявляющих интерес к результатам своей деятельности (мотив избегания – свидетельствовал о боязни показать низкий результат в процессе выполнения лабораторной работы; состязательный мотив – показывал, насколько студент придает значение высоким результатам в деятельности одногруппников, мотив самоуважения – выражал стремление испытуемого ставить перед собой все более и более трудные цели в однотипной деятельности).

Перечисленные выше компоненты, составляющие ядро мотивационной сферы личности, выступали в роли факторов, непосредственно побуждающих студентов к определенному виду деятельности. В нашем случае, в результате самостоятельной работы и выполнения лабораторной работы, по освоению материала по теме «Метод наименьших квадратов». В качестве мотивационных компонентов мы рассматривали также и такие как, значимость результатов, сложность задания, волевое усилие, оценка уровней достигнутых результатов, оценка своего потенциала, намеченный уровень мобилизации усилий, ожидаемый уровень результатов, закономерность результатов – выражающаяся пониманием студентов собственных возможностей в достижении поставленных целей, инициативность.

В нашей работе использовались элементы методики выявления уровней сформированности мотивационно-потребностной сферы в плане использования компьютерных технологий, подробно рассмотренной в различных педагогических исследованиях [4].

В экспериментальных группах у студентов возникла осознанная потребность в применении компьютерных технологий в изучении математики, в которых они увидели новое образовательное средство, помогающее максимально реализовать свои способности и быстро решить поставленную задачу.

Необходимость исследования уровня рефлексии вызвана тем, что самостоятельная деятельность лежала в основе выполнения работы. Использование критерия U Манна-Уитни позволило выявить различия между контрольными и экспериментальными группами по уровню рефлексии. Не вдаваясь в подробности вычислений значения критерия, отметим только, что он показал: студенты экспериментальной группы превосходят студентов контрольной группы по уровню рефлексии [5].

Таким образом, на основе проведенного анализа можно сделать вывод, что реализация компетентностного подхода в организации самостоятельной работы сту- дентов оказывает положительное влияние на мотивационные потребности студентов как в плане обучения вообще, так и в использовании компьютерных технологий, а также способствует формированию рефлексивной позиции.

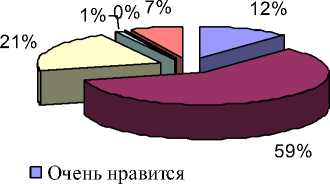
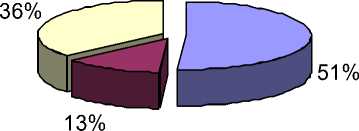
Кроме того, среди студентов экспериментальных групп было проведено анкетирование на предмет удовлетворенности предложенной методикой, результаты которого приведены на диаграммах 1, 2, 3, 4.

Диагра

В какой мере Вам нравится выпо лабораторные работы в проце изучения высшей математик

Диаграмма 2

Уменьшает ли использование задач с практическим содержанием время, затрачиваемое вами на изучение материала?

• □    Нравится

• □    Скорее нравится, чем не нрави

• □    Скорее не нравится, чем нрави

• □    Совсем не нравится

• □    Не знаю

Диа

Как Вы оцениваете роль лабор в изучении математике

28%

1%

20%

24%

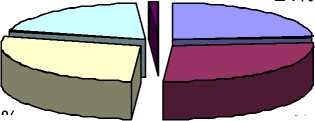
27%

• □    Помогает лучше запомнить учебный материал

• □    Учит решать практические

• □    Да

• □    Нет

• □    Затрудняюсь ответить

Диаграмма 4

Вам хотелось бы иметь пакет лабораторных по высшей математике дома для самостоятельной работы?

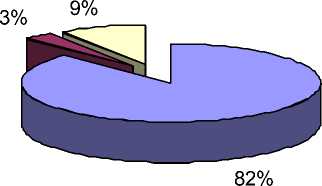
• □    Учит работать совместно с программами

D Повышает интерес к изуче высшей математики

• □    Не играет никакой роли

  □ Да

  □ Нет

  □ Не знаю

  
  

Результаты анкетирования отражают позитивное отношение студентов экспериментальных групп к предлагаемой методике.

Заключение

Исследование возможностей компетентностного подхода и условий его эффективного использования является весьма актуальным. По нашему мнению, приме- нительно к организации самостоятельной работы студентов на лабораторных работах по математике стоит вопрос поиска способов индивидуализации обучения, подразумевающей не только ориентацию на профессиональную принадлежность студентов, но и учет личностных особенностей студентов. Это ведет, во-первых, к вопросу о диверсификации и вариативности предлагаемых заданий, во-вторых, к вопросу о пошаговом контроле результатов обучения. При этом студент должен выступать субъектом обучения, тогда возможно говорить о формировании у него механизмов самоуправления в профессиональном становлении.