Компьютерная графика, порожденная линейными преобразованиями координат

Задача компьютерной графики заключается в моделировании движения объектов в пространстве, то есть в моделировании их поступательных и вращательных перемещений, а также возможного изменения масштаба. В [1] для решения отмеченных задач, а также задач отображения объектов предполагается применить матричную алгебру. Авторы настоящей работы считают, что более естественной, а главное, более простой технологией решений поставленных задач является технология, опирающаяся на линейные преобразования координат.

Рассмотрим прежде всего преобразование, которое отвечает за вращение объекта вокруг некоторой оси. Как показал опыт решения задач классической механики, для этой цели удобнее всего пользоваться подходом Эйлера [2] (задачи динамики твердого тела). С подвижным объектом свяжем ортогональную декартову систему координат 0 xyz , а систему 0ξηζ, имеющую то же начало, свяжем с пространством, в котором осуществляется движение. Эту последнюю систему называют обычно неподвижной или абсолютной.

Координаты точек объекта в обеих этих системах связаны между собой соотношениями [3]:

• 2 , = a1 x + ОС2 y + ОС ₃ z ,

  
  

П = 31 ^x + 32 ^y + 33 ^{z ,}

= Y 1 ^x + Y2 ^y + Y₃ z .

В представленной записи α 1 , α 2 , α 3 – направляющие косинусы осей 0 xyz по отношению к оси 0ξ; β 1 , β 2 , β 3 – те же величины по отношению к оси 0η; γ 1 , γ 2 , γ 3 – направляющие косинусы подвижных осей по отношению к оси 0ζ. Эти девять величин Эйлер предложил определять через три независимые угловые координаты θ, ψ, φ, получившие впоследствии название углов Эйлера:

CL1  cos Ф * cos О • cos v — sin ф * sin ф, ос2 cos Ф • cos О • sin Ф — sin Ф • cos Ф,

CL ₃ cos Ф • sin О,

• 3    ₁  sin Ф • cos О • cos V + cos ф • sin ф,

з 2 sin ф • cos о • sin ч^ + cos ф • cos ф,

• з₃   sin ф • sin о,

Y 1 sin О • cos Ф,Y 2   sin О • sin Ф,Y3   cos .

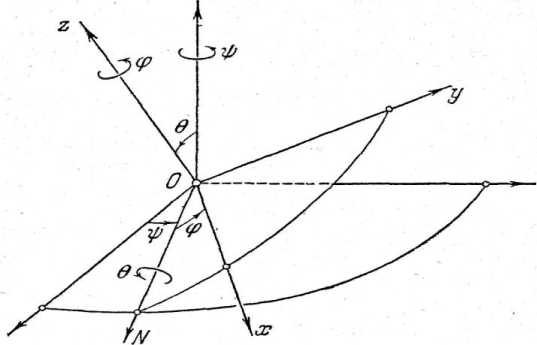
Рис. 1. Взаимное расположение подвижной и неподвижной систем отсчета, определяемое углами

Эйлера

Углы, показанные на рисунке 1, называются: φ – угол собственного вращения, ψ – угол прецессии; θ – угол нутации. Задавая θ из интервала [0, π], мы отклоняем тело и связанную с ним ось 0 z от оси 0ζ на соответствующий угол θ. Задавая, кроме этого, ψ из интервала [0, 2π], мы поворачиваем на ψ систему координат 0 xyz вокруг оси 0ξ. Наконец, фиксируя еще значение φ в интервале [0, 2π], мы поворачиваем тело вокруг оси собственного вращения (оси 0 z ). Таким образом моделируются все возможные повороты перемещающегося и видоизменяющегося объекта.

Если правые части (1) умножить на числа a 1 , a 2 , a 3 , то мы изменим масштабы объекта по осям 0ξ, 0η, 0ζ соответственно. Наряду с этим добавим к правым частям (1) постоянные величины b 1 , b 2 , b 3 . Это обеспечит сдвиг объекта по соответствующим осям.

Таким образом, результирующие формулы поворота, масштабирования и сдвига будут выглядеть как формулы линейного преобразования:

• 1' x      '2 y      3' zb

  
  

• 1' x     '2y     3' zb

• 1' x     '2y     3' zb

Здесь   i'    ai i,     i'    ai i,     i'    ai i, i 1,2,3 .(4)

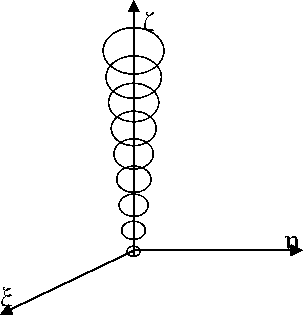
Рис. 2. Подъем газового пузыря по вертикальной траектории

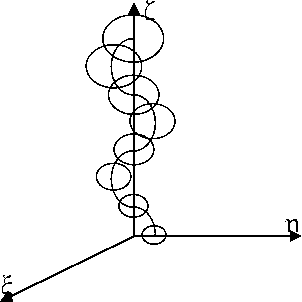
Рис. 3. Движение пузыря по спирали

Движение объекта, показанное на рис. 2, определяется его перемещением вдоль оси 0ζ и одновременным изменением масштаба по всем трем координатным осям 0 x , 0 y , 0 z . Нетрудно понять, что пропорционального со временем роста размера пузыря можно добиться, задав коэффициенты a i , входящие в (4) следующим образом:

a_i = 1 + v ₀ t ,    i 1,2,3 .                                  (5)

Здесь v 0 – относительная скорость роста линейного размера пузырька.

В рассматриваемом примере в начальный момент времени центр сферы находится в центре O , являющемся началом систем отсчета (рис. 1), а в последующие моменты времени он всегда находится на оси 0ζ. Поэтому зависимости углов Эйлера от времени могут быть следующими:

е = 0, ф = ф t _,           t .               (6)

Здесь ввиду полярной симметрии объекта функции φ( t ) и ψ( t ) могут быть произвольными, в частности они могут быть нулями: ф t 0 , ^и t 0 .

Перемещение сферы по оси 0ζ задается следующими коэффициентами:

b ₁    b ₂    0, b 3    _wt .                        (7)

где w – скорость движения центра сферы по оси 0ζ.

Движение объекта на рис. 3 является более сложным. Здесь центр сферы перемещается по винтовой линии. При этом с высотой пузырек также увеличивается в размерах. Все метаморфозы, происходящие со сферой, в этом случае описываются параметрическими зависимостями для коэффициентов (5), (6). Причем в этом случае целесообразно принять ф tt ,\|/ t 0 . Зависимости (7) обобщаются и принимают следующий вид:

b ₁    x _0, b ₂    y ₀ ,   b ₃    wt .                  (7’)

Здесь x 0 , y 0 – координаты (не равные нулю), определяющие начальное положение сферы.

Сам объект (сфера) может быть параметризован следующим образом:

x  x   R sinX cos 5,

• y  y   R sin X sin 5,

• z wt R cos X.

Здесь угловые параметры λ и δ изменяются в следующих диапазонах:    X е 0,  ,      0, 271 .