Компьютерная организация и диагностика бинарного взаимодействия обучающихся решению задач

Коммуникативные способности учащихся особенно ярко раскрываются при коллективном способе обучения [1], который имеет четыре формы информационного взаимодействия: коллективную (каждый учит каждого), групповую (один одновременно учит многих), бинарную или парную (один учит другого) и индивидуальную.

В результате коммуникаций между участниками процесса обучения эффективно усваиваются знания, умения, навыки. При этом развиваются коммуникативные качества личности. Обучение идет с учетом разного материала и индивидуальных особенностей, на основе коммуникативности и полной самостоятельности обучающихся; усвоение и применение максимально приближены. Предполагается, что обучение решению задач имеет итеративный характер. [2]. В результате повторяющихся упражнений совершенствуются навыки логического мышления и понимания; развиваются навыки мыследеятельности, включается работа памяти, идет мобилизация и актуализация предшествующего опыта и знаний; повышается ответственность не только за свои успехи, но и за результаты коллективного труда; формируется адекватная самооценка личности, своих возможностей и способностей, достоинств и ограничений; обсуждение одной информации с несколькими сменными партнерами увеличивает число ассоциативных связей, следовательно, обеспечивает более прочное усвоение.

Бинарная форма организации обучения основана на бинарном характере взаимодействия людей в жизни. Сущность бинарной формы организации обучения: в каждый конкретный момент времени один ученик обучает, другой учится, либо вместе обучаются, помогая друг другу. В работе участвуют либо два ученика, либо ученик и учитель (статическая пара). Статическая пара, как правило, состоит из учеников, сидящих за одной партой. Иногда пары формируются по желанию или без желания учеников. Однако фактор контактности и доброжелательности играет в бинарной форме организации обучения решающую роль. Статическая пара является школой подготовки к работе в коллективной форме организации обучения. В паре ученики постоянно меняются ролями учителя и ученика. Они могут обучать друг друга в режиме взаимообучения, контролировать друг друга, проверять домашнее задание, сообщать новый материал, готовить к зачету, закреплять изученное и т.п.

Статическая пара является одним из наиболее эффективных механизмов, обеспечивающих регулярное общение учащихся друг с другом на уроке и соответственно значительное повышение речевой и мыслительной активности каждого ученика. Каждый получает возможность на каждом уроке говорить, отвечать, объяснять, доказывать, подсказывать, проверять, оценивать, корректировать ошибки в момент их возникновения, воспринимать содержание речи партнера, отвечать на вопросы и задавать их.

Совместная деятельность и общение являются решающими факторами развития самосознания учащихся благодаря тому, что учащиеся становятся субъектами взаимного межличностного отражения отношений и взаимодействий. Одним из условий успешного управления учебно-познавательной деятельностью учащихся при использовании коллективных учебных занятий является качественный дидактический материал. Обычно он включал карточки, составленные для методик взаимообмена заданиями и взаимопроверки индивидуальных заданий, и карточек для контроля усвоения знаний и умений. Однако необходимость создания материала, «заменяющего учителя», приводит к большим временным затратам. Кроме этого, возникает еще одна проблема – оценка учащихся за проделанную ими работу. Следовательно, нужен инструмент, который позволял бы ученикам работать в паре без вмешательства учителя, а с другой стороны, позволял бы учителю отслеживать все действия, производимые учащимися, и выставлять оценку, соответствующую этим действиям. На наш взгляд, таким инструментом являются сетевые динамические тесты-тренажеры (СДКТТ). [3].

Теоретическая часть

Рассмотрим организацию сетевых динамических компьютерных тестов-тренажеров, которые представляют собой систему программно связанных между собой соответствующих динамических компьютерных тестов-тренажеров. [4].

Ученик, работая с системой, выполняет все многообразие заданий тестируемой темы. Каждое задание в СДКТ представляет собой компьютерную систему, в которой имеются все атрибуты управления учебным процессом с соответствующим контролем и диагностикой, который проводится в процессе деятельности по выполнению задания. Операции или математические действия представлены в таких заданиях, как временной ряд событий. Последовательность этих событий управляется с помощью компьютера, посредством специальным образом организованной обратной связи. Адаптация проводится через варьирование суммарного коэффициента обратной связи, который изменяется в зависимости от успешности учебной деятельности ученика. [4, 5].

Процесс учебной деятельности при решении задач мы рассматриваем, как процесс, при котором суммарный коэффициент обратной информационной связи R уменьшается от 1 до 0. Другими словами, по мере обучения, ученику требуется все меньше и меньше «подсказок» (т.е. информации о процессе деятельности). Одновременно с уменьшением частоты подкреплений происходит уменьшение количества ошибочных действий. В пределе, когда ученик овладел алгоритмом, он не нуждается в информационных подкреплениях учебной деятельности. При R=0 деятельность ученика становится автономной, независимой от других участников процесса научения. В этом случае можно с уверенностью сказать, что он овладел умением осуществлять алгоритмическую деятельность по выполнению данного типа заданий. [6] .

В предлагаемых нами сетевых динамических тестах-тренажерах управление местной обратной связью берет на себя либо учитель, либо ученик, играющий роль учителя. Коэффициент местной обратной связи равен RM = Pi 1 ■ pi 1.

Главная петля обратной связи определяет функцию, определяющую уровень самостоятельности деятельности учащегося. Коэффициент главной обратной связи pi-i задается компьютерной системой. Он равен B . Суммарный коэффициент обратной связи при выполнении i задания равен

R i = P A ^{- 1}

. pi ^{- 1}   . p i ^{- 1}

¹ B + ¹ A ,

где P^l i ¹

N

l - 1

N

l - 1

– доля неправильных действий

(^N 1 –

количество неправильных

действий;    0 – информационных

p i ^{- 1}

общее количество действий); B – относительная частота воздействий учителя посредством включения датчиков

«расстояние до цели». [7, 8]. В этом случае компьютер, учитывая относительную

P i ^{- 1}

частоту ошибочных действий B переводит ученика на новый уровень самостоятельности. Учитель должен оптимальным образом регулировать число управляющих воздействий, т.к. слишком частые воздействия могут сбросить успешного ученика вниз, а слишком редкие воздействия или их отсутствие могут не дать возможности слабому ученику выполнить задание.

Практическая часть

Рассмотрим работу сетевого динамического теста-тренажера на примере СДКТТ «Преобразование графика квадратичной функции», позволяющего организовать деятельность ученика по выработке алгоритма преобразования графика функции y = x в график функции y a (x x0)

y ⁰ . Для этого на экран

монитора выводится геометрический образ функции y = x . С помощью управляющих кнопок ученик может осуществлять параллельный перенос, деформировать и переворачивать параболу. По окончании преобразований он вводит ответ нажатием кнопки «Готово» Тренажер может работать в трех режимах.

• 1.    В тестировании участвуют учитель и ученик (статическая пара).

• 2.    В тестировании участвуют два ученика, исполняющие роль учителя по

  очереди.

  
  

• 3.    В тестировании участвуют два ученика, одновременно решающие задачу,

генерируемую компьютером.

Рассмотрим более подробно 1 и 2 режимы на примере сетевого динамического теста-тренажера «Преобразование графика квадратичной функции» (рис. 1).

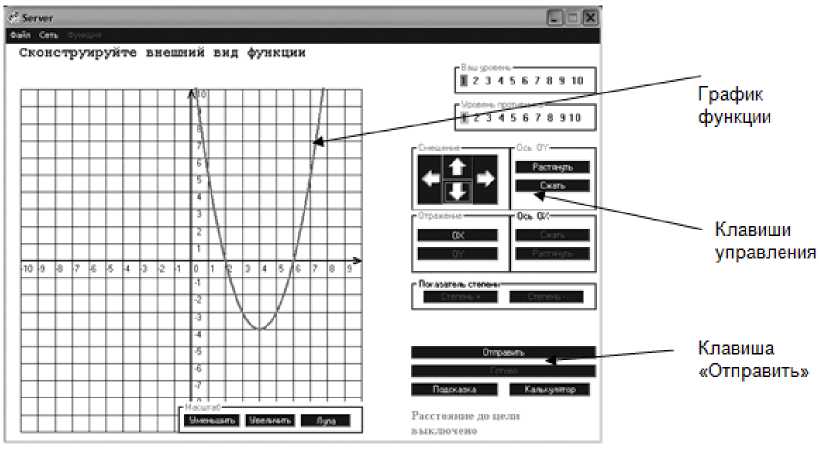
Рис. 1. Конструирование задания.

Режим 1. За компьютерами сидят учитель и ученик или ученик и ученик. На экран дисплея учителя выводится геометрический образ функции y = x . С помощью управляющих кнопок учитель может смещать, деформировать и переворачивать параболу (рис. 1.). По окончании преобразований он отправляет задание ученику.

При этом компьютер рассчитывает параметры квадратичной функции a , x₀ , y₀ и преобразует уравнение функции к виду y = ax + bx + c . После этого ученику выводятся на экран уравнение и график функции y = x , преобразуя который, ученик должен получить график сконструированной функции (рис. 2).

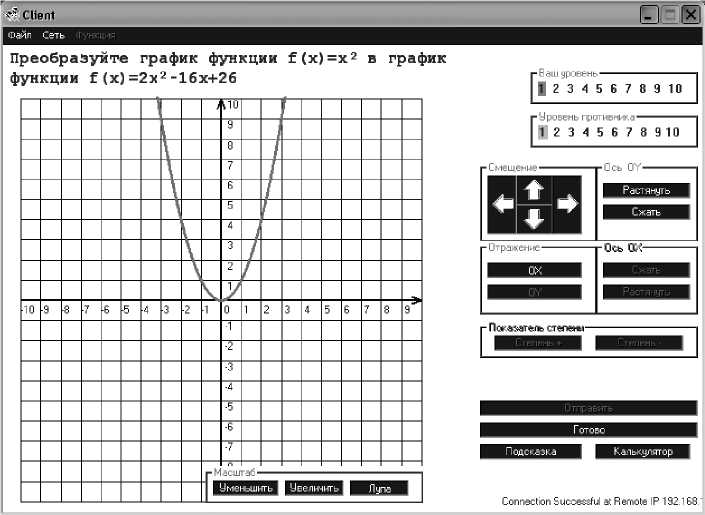
Рис. 2. Задание, полученное учеником.

В каждом задании можно выделить конечное число элементарных операций. Это сдвиги вправо, влево, вверх, вниз, переворот, связанный с изменением знака коэффициента, сжатие и растяжение. Каждая операция выполняется по нажатию определенной клавиши на панели управления. В программе, согласно которой ученик выполняет это преобразование, производится запись кодов клавиш операций. [3].

Запись последовательности нажатий производится скрытно от ученика и позволяет записать траекторию решения задачи. Процесс записи производится с хронометражем времени, затрачиваемого на каждую операцию.

Все действия ученика отображаются на мониторе учителя, и учитель, анализируя деятельность ученика, может подавать сигналы, помогающие ученику сделать правильный ход (рис. 3).

Изучая динамику изменения учебной деятельности ученика по достижении цели, например, преобразования графика функции, учитель может сделать выводы о том, как быстро ученик осваивает алгоритм. Таким образом, учитель получает информацию о скорости обучения ученика. В отличие от метода протокола записи решения задачи, используемой в психологии, компьютерная запись решения задачи с числовыми характеристиками - количество действий, ошибок, времени, затрачиваемого на каждый ход, позволяет исключить влияние субъективного фактора.

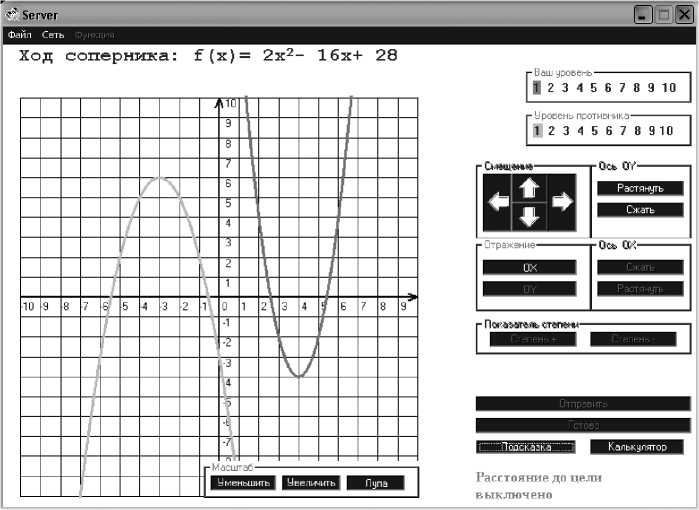
Рис. 3. Ход решения на мониторе учителя.

В обучении очень важную роль играет учет отклонений от заданной алгоритмом последовательности действий. Как правило, отклонения приводят к ошибке. Цель при этом не достигается. Цикличность в создании учебных заданий и отлаженная обратная связь позволяет ученику: во-первых, увидеть эти отклонения, во-вторых, скорректировать ход решения очередного задания с учетом ошибки. В простейшем случае обратная связь представлена информацией, выведенной на экран компьютера в виде:

• 1)    сообщения, типа «правильно, неправильно»;

• 2)    графика верного решения, представленного другим цветом.

При работе с СДКТ ученик, выполняя тестовые задания, изменяется в плане совершенствования алгоритмической деятельности. Эти преобразования объекта фиксируются компьютером в реальном времени, образуя временной ряд событий. Если ученик работает с тренажером по алгебре, то у него происходит преобразование состояния, которое заключается в том, что от задания к заданию он делает все меньше и меньше ошибок. В идеале он осваивает алгоритм выполнения заданий и не совершает ни одной ошибки.

Проведем анализ возможности сетевых компьютерных технологий обучения для организации информационного взаимодействия обучающихся решению задач для третьего режима работы СДКТТ. В этом режиме учащиеся совместно решают задачу, осуществляя действия по очереди. Рассмотрим относительно простую систему сетевого компьютерного динамического тестирования деятельности двух обучающихся решению задач, так называемое парное или бинарное взаимодействие. [3, 5].

В качестве численной характеристики процесса научения используется целевая функцию ^ф . Целевая функция ФГО каждого ученика в момент времени t i + i = t i ^{+ A t} i + i определяется уравнением

Ф (Г ⁺A t , + i ) = ^ф ( ф (1₁),8(1₁ + A t_{i +} i )) , (2)

где S(t) - функция вознаграждения ученика. Она равна сумме поощрений (1)

и штрафов (0), полученных учеником в процессе выполнения i + 1 задания.

Выходной сигнал

f ( t )

формируется функцией F

f ( t i ) = F [ ф ( t , )]

Выходной сигнал определяет вид и частоту помощи, которую система управления оказывает обучающемуся. Частота помощи или подкрепления деятельности ученика зависит от достигнутого значения целевой функции.

За акт поведения пары учащихся были взяты два последовательно совершаемых действия: действие первого ученика и последующее за ним действие второго ученика. Так как каждый ученик может выполнить как правильное (1), так и неправильное (0) действие, предлагается использовать следующее обозначение для типов актов поведения пары:

• 1- 1, каждый из учеников выполнил действие правильно;

• 0- 1, первый ученик ошибся, второй исправил ошибочное действие;

• 1- 0, первый ученик выполнил действие правильно, второй нет;

• 0- 0, оба ученика выполнили неверные действия.

В качестве целевой функции ^ф управления поведением пары обучающихся можно использовать информационную энтропию:

4                         n

Ф = H = Z P i log₂ P i ,       p i = -i-

i=i              где       n pi - вероятность каждого типа возможных актов поведения пары, ni - число актов поведения каждого из возможных исходов (0-0, 1-0, 0-1, 1-1), n - общее из возможных актов поведения.

Для более наглядного отображения достижений пары учащихся разобьем значения целевой функции на 10 интервалов и назовем их уровнями самостоятельности.

Переход между уровнями зависит от рассчитанной компьютером целевой функции и определяется формулой

L = (1 - f )9 + 1

где L - уровень самостоятельности, f - целевая функция.

Структурная схема системы управления информационным взаимодействием пары обучающихся решению задач представлена на рис. 4. Прямоугольниками обозначены программные модули, а стрелками - информационные потоки.

В зависимости от уровня самостоятельности компьютерная система оказывает на каждого из учащихся управляющие воздействия (через индикатор расстояния до цели). Цель деятельности управляющей системы состоит в том, чтобы вывести ученика на уровень, который отвечает полной самостоятельности ученика.

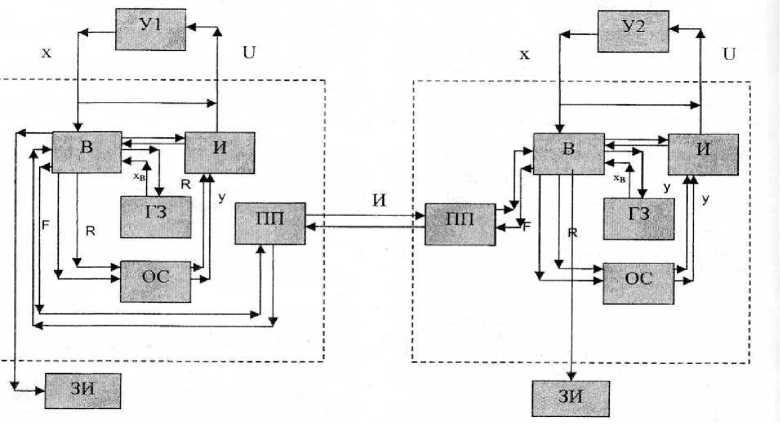
Рис. 4. Структурная схема обучающей и диагностирующей системы: ГЗ -генератор заданий; ПП - приемо-передающий модуль; В - вычислительный модуль; И - интерфейсный модуль; ОС - модуль отрицательной обратной связи; У1 - объект управления (первый ученик); У2 - объект управления (второй ученик); ЗИ - аналитический модуль, записывающий информацию о деятельности ученика; хвх - задающие воздействие (задание); и - управляющее воздействие; х - управляемая величина; R - критерий оптимальности; F-,-функционалы, определяющие текущее состояние решения задачи в ее проблемном пространстве; у - корректирующее воздействие; И - информация для передачи

Анализ и оценка разработки

На рис. 5 показана реализация целевой функции обучающейся пары и функции траектории деятельности системы управления y ( t ) . ^{L ( t )} и частота управляющих воздействий ^{y ( t )}. Вертикальные линии соответствуют окончанию выполнения

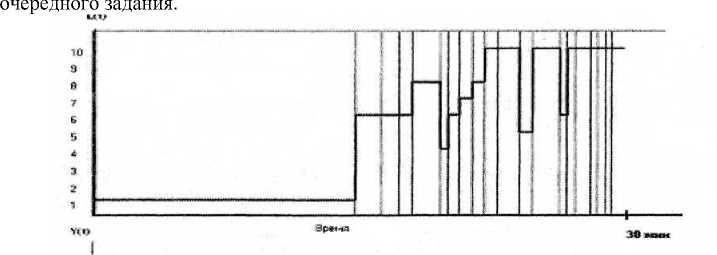
а

б

Рис. 5. Экспериментальный график уровней самостоятельности а и

частоты управляющих воздействий б.

Функция вознаграждения (рис.6) определяет отображение каждого действия для данной задачи в данный момент времени. Если пара учащихся правильно выполняет действие, то график возрастает на два (действие каждого из учеников увеличивают значение функции на единицу), если неправильно - убывает на два. В случае, если один учащийся выполнил правильное действие, а другой - нет, то значение функции вознаграждения не изменяется.

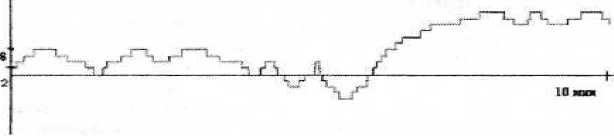
Рис. 6 График функции вознаграждения пары учащихся .

Ширина ступенек показывает время, которое учащийся затратил на выполнение данного действия. Функция вознаграждения постоянно возрастает в случае выполнения учащимся всех действий правильно и убывает, если действия выполнены неверно.

На рис. 7 представлены диаграммы действий пары на разных этапах тестирования. На первой диаграмме показано одно из первых заданий, учащиеся действуют несогласованно, методом проб и ошибок их информационная энтропия стремится к 1.

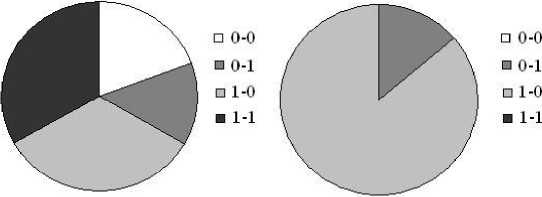
Рис. 7 - Диаграммы типов актов поведения пары учащихся.

На второй диаграмме в паре происходит разделение учащихся на ведущего (ученик 1) и ведомого (ученик 2), причем видно, что ведущий не только совершает все действия без ошибок (вариантов 0-0 и 1-0 на диаграмме нет), но и исправляет ошибочные действия ведомого, в результате чего энтропия пары уменьшается.

Заключение

Анализируя экспериментальные данные - диаграммы, графики, можно сделать выводы об эффективности объединения данных учеников в пары. Например, пары, в которых целевая функция на протяжении всего тестирования постоянно увеличивается - эффективны, а пары, в которых она постоянна или совершает колебания - неэффективны. Такие пары желательно перераспределить. Эксперимент показал, что технологию сетевых динамических компьютерных тестов-тренажеров целесообразно использовать как эффективное средство повышения и диагностики коммуникативных способностей обучающихся.