Компьютерная поддержка решения вероятностных задач из истории математики

КОМПЬЮТЕРНАЯ ПОДДЕРЖКА РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ ИЗ ИСТОРИИ МАТЕМАТИКИ из 25. Каким ему лучше зайти в аудиторию: первым или четвертым, если выбранные до него билеты не возвращаются? В каком случае вероятность взять выученный билет будет больше?».

Попробуем ответить на вопросы с педагогической точки зрения: допустима ли такая схема проведения экзамена с позиций объективности выставляемой оценки; возможно ли, что экзамены для обучающихся обладают заведомо математически противоречивыми исходами; возможно ли, что предлагаемая схема фальсифицируема с точки зрения равновозмож-ности событий? С точки зрения педагогических измерений шанс сдать экзамен не должен зависеть от очередности его сдачи студентами [1; 3; 10]. Иначе экзамены надо отменять.

Рассмотрим ответы на поставленные вопросы на основе принципа верификации сходной более общей математической задачи с использованием компьютерной поддержки (GeoGebra) [4] с учетом некоторых сведений из истории вероятностей [6; 9]. Поскольку данная задача популярна и рассматривается во многих задачниках по теории вероятностей, ее варианты приводят многие интернет-издания, мы кратко остановимся на математическом инструментарии решения.

Пусть некоторое событие А может произойти лишь при условии появления одного из попарно несовместных событий H_t , называемых гипотезами и образующих полную группу. Заранее неизвестно, какое из этих событий произойдет. Требуется найти вероятность события А .

По определению: H ₁ + H ₂ + ... + + H_n = Ω , где Ω – достоверное событие, тогда событие А можно представить в виде:

A = A Ω = A ( H ₁ + H ₂ + ...+ H_n ) =

= AH ₁ + AH ₂ + ...+ AH_n , где в правой части равенства сумма несовместных событий, так как

( AH_i )( AH_j ) = A ( H_iH_j ) = A ∅ = ∅ ,

тогда

n

P ( A ) = £ A • H , = t = 1

n

= Z P ( H t l P . C A ) . t = 1

Получили формулу полной вероятности:

n

^P ( A ) = £ P ( Hl ) P H . ( A ) .

k = 1

Прейдем к решению приведенной задачи. Пусть событие А – студент сдал экзамен выбрав знакомый билет.

Если наш гипотетический сту-

дент зайдет на экзамен первым,

то

^P ( ^A ) =

. Если он зай- 5

дет вторым, то о первом студенте

можно выдвинуть две гипотезы:

H ₁ – взял знакомый нашему студенту билет, H ₂ – взял невыученный билет. Тогда по формуле полной вероятности находим:

Z X 4 Z X 1

^P ( ^H i ) = 5; ^P ( ^H 2 ) = 5;

P ( A ) = 19; P ( A ) = — ;

^{H 1}        24 ^{H 2}        24

p ( a ) = 4 . 19 +^

5 24 5 24

Вычисляем по формуле полной

вероятности:

P ( A ) = ¹⁹

18 10 19

--+---+

23 30 23

1 20 12  4

+----= — = —.

30 23 15  5

Если наш студент зайдет четвертым, то относительно обучающихся, зашедших до него, необходимо рассмотреть следующие гипотезы: H_t взяли 4 – t выученных билета и t – 1 неврученных билета, где t принимает значения от 1 до 3. Тогда

30 P ( H 1 ) = ^ 20;3 ^ 5 C 25	57 = 115;
21 P ( H 2 ) = ^ 203 ^ 5 C 25	= 19. = 46;
12 P ( H з ) = C 20^ C 25	_ = 276;
03 P ( H 4 ) = C 20; ?5-C 25	1 = 230.

1 20

Используя формулу полной вероятности находим:

P ( A ) =	57	17	19	18
		+	^^^^^^^^— e	+
	115 "	22	46	22
1	19	1	20	4
+--	--+	^^^^^^^^^^^^— «	—	= —.
276	22	230	22	5

Если наш студент зайдет третьим, то относительно первых двух студентов можно предположить: гипотеза H ₁ – взяли два выученных нашим студентом билета, H ₂ – взяли один знакомый, один незнакомый билет, H ₃ – взяли два невыученных билета, тогда:

P(H ) = Ck = 20! . 2! 23! = 19. ( 1) C25 2118! 25!30;

PH U CVе5 = 20■ 5■ 2!23! = 10. ( 2)     C25          25!30;

p(h )=C2 = 5^_2k = ±. v 37 C25 2!3! 25!30 ’

P H1 ( A ) = 23; P H 2 ( A ) = 13;

P ( A ) = ²⁰

^{H 3}        23

Видно, что во всех четырех рассмотренных случаях вероятность получить выученный билет одна и та же, то есть «обмануть удачу» нельзя. Тогда возникает вопрос: а может «везение» улыбнется студенту, если он зайдет на экзамен в числе последних? Но в этом случае может случиться, что оставшихся выученных билетов для него будет меньше.

Приведем общее решение подобных задач, так как оно интересно не только студентам, но и преподавателям, с точки зрения объективности выставляемой оценки. Итак, студент выучил m билетов из общего количества – n, предполагаем, что m ≤ n . Требуется найти вероятность успеха студента, если он заходит на экзамен k -тым, где k ≤ n , где m и n , k можно рассматривать как натуральные параметры.

Реализация формулы полной ве- роятности в рекуррентной форме определяется формулами:

P ( H t ) =

f k — t     t — 1

m   n- m — m k—1

,

P H t ( A ) =

m + 1 - k n + 1 - k

то есть:

n     k - t     t - 1

m + 1 - k n + 1 - k ’

где

k -1 < m, t = 1, k i <

t - 1 <  n -

m,.

k < n.

Реализацию полученной рекуррентной формулы проведем в системе компьютерной алгебры Geogebra (Рисунок 1). Опишем ход выполнения работы. Инструментом «Ползунок» разместим на полотне четыре ползунка с именами k , m , n , t для динамического задания соответствующих величин. Через панель «Настройки» зададим свойства ползунков: минимальное значение – 0, максимальное значение – 50, шаг – 1, для ползунка t минимальное значение – 1, максимальное значение – k , шаг – 1. Затем в строке ввода разместим выражение нахождения слагаемых искомой суммы:

PHt = (nCr(m, k – t) nCr(n – m, t – 1)) / nCr(n, k – 1) (m + t – k) / (n + 1 – k).

Следующим шагом в данной строке введем выражение для нахождения последовательности слагаемых, воспользовавшись командой «Последовательность, выражение, переменная, начальное значение, конечное значение»:

fk = Последовательность ((nCr(m, k – t) nCr(n – m, t – 1)) / nCr(n, k – 1) (m + t – k) / (n + 1 – k), t, 1, k).

После чего в той же строке введем выражение нахождения полной вероятности как сумму членов последовательности:

Сумма(fk)

и также выражение нахождения вероятности гипотез по формуле Байеса:

Последовательность(fk / P, k, 1, 1)

Приступим к вычислениям: как «удача» нашего студента позволяет ему оценивать H_t действия его одногруппников по отношению к нему. В общем случае вычисления достаточно объемные. Воспользуемся составленной нами программой, в которой мы можем легко менять параметры m , n , k . Допустим, изменяем k – очередность входа на экзамен при неизменных величинах m , n (см. Рисунки 2 и 3).

Итак, вероятность «успеха» студента неизменна, но «помощь» од-ногоруппников возрастает – вероятность уменьшить количество его выученных билетов снижается.

Изменяем m – число выученных билетов при неизменных k , n (см. Рисунки 4 и 5).

Таким образом, верификация утверждения алгоритма обновления гипотез по формуле Байеса подтверждается и реализуется достаточно легко с применением выбранной системы компьютерной алгебры. На наш взгляд, также представляет интерес задача с вероятностью «невезения». Однако в каждой ситуации необходимо помнить крылатое изречение: «Существует три вида лжи: ложь, наглая ложь и статистика» (Г. Лабушер, М. Твен).

Итак, можем констатировать, что проектирование подобного комплекса задач будет полезным средством в образовательной среде для обеспечения качества учебновоспитательного процесса и формирования информационных компетенций средствами математики, а также для организации научно-исследовательской деятельности обучающихся. Рассматриваемая система GeoGebra является эффективным инструментом в реализации компьютерной поддержки решения математических задач: вычислительных задач по теории вероятностей и математической стати- стике, в конструктивных задачах геометрии, например, в построении эволюты и эвольвенты [4] и многих других. Предложенная компьютерная поддержка системы в решении математических задач позволяет обучающимся прийти к более глубокому пониманию раздела теории вероятностей или любого другого раздела математики. При этом информатика выступает как инструмент формирования учебно-познавательных компетенций. На наш взгляд, использование подобных программных продуктов для решения прикладных задач принесет пользу не только студентам педагогических вузов, но и преподавателям математики.

С точки зрения формирования у студентов требуемых образовательным стандартом компетенций, нами проведено экспериментальное проектирование комплекса заданий в рассматриваемой системе в рамках изучения математических дисциплин: «Теория вероятностей», «Алгебра», «Геометрия». Задания разработаны для студентов 2 курса Набережночелнинского государственного педагогического университета по программе подготовки бакалавров по направлению 44.03.05 «Педагогическое образование», профили «Математика» и «Информатика»). Проанализировав существующие учебные программы, можно заметить, что наблюдается некоторая разобщенность математических дисциплин и дисциплин из цикла «Информатика и программирование». Преподавание этих дисциплин ведется в разных семестрах и на разных курсах, либо эти дисциплины осваиваются параллельно, но без должной интеграции. Для нас очевидно, что интегрирование этих дисциплин должна осуществляться с первых курсов.

Одним из элементов интеграции выступает аппарат вычислительной информатики и специализированных компьютерных программ. Подобные программы, используемые на заняти-

КОМПЬЮТЕРНАЯ ПОДДЕРЖКА РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ ИЗ ИСТОРИИ МАТЕМАТИКИ

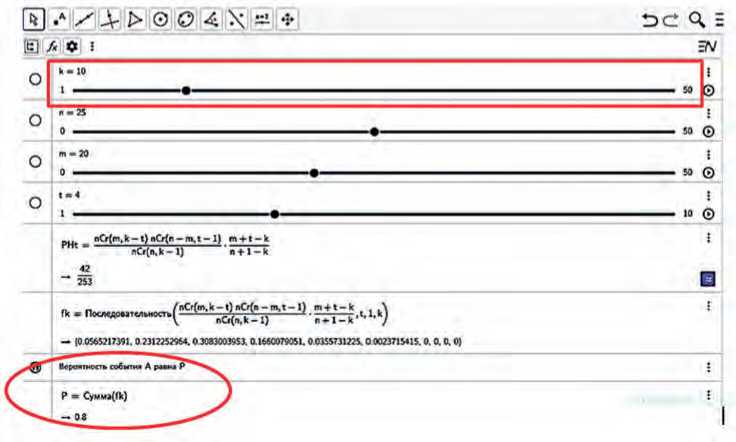
Рисунок 1. Вычисление вероятности выбора студентом выученного билета

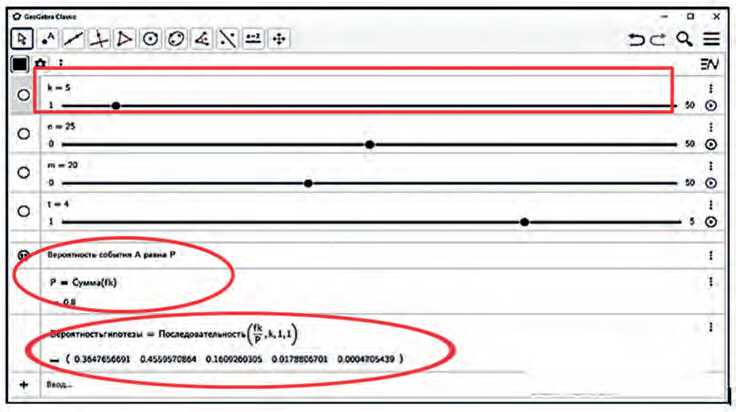
Рисунок 2. Вероятности гипотез при k = 5

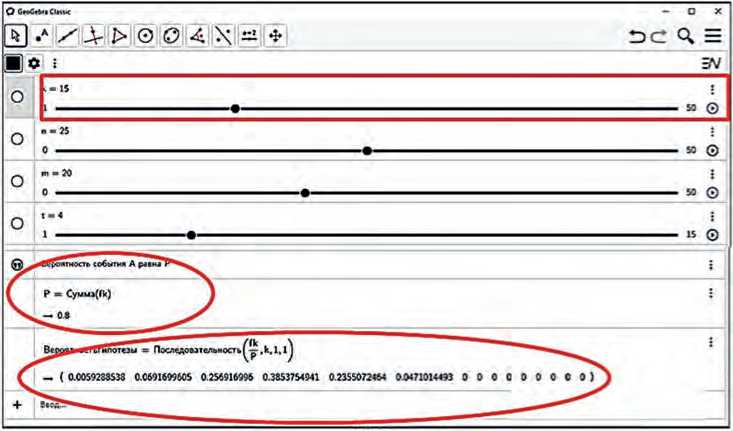
Рисунок 3. Вероятности гипотез при k = 15

Рисунок 4. Вероятности гипотез при m = 10

Рисунок 5. Вероятности гипотез при m = 15

ях по информатике, реализующие методы высшей алгебры и математического анализа, теории вероятностей и математической статистики, служат необ- ходимым интегрирующим звеном в преподавании вузовских курсов естественно-математических и общетехнических дисциплин, имеющих эмпирическую основу. Систему GeoGebra в силу ее доступности можно использовать в качестве первоначального инструментария в рамках реализации этих требований.

КОМПЬЮТЕРНАЯ ПОДДЕРЖКА РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ ИЗ ИСТОРИИ МАТЕМАТИКИ