Компьютерное моделирование оптических систем в курсе общей физики

где т = 2/7 - число преломляющих поверхностей элементов системы;

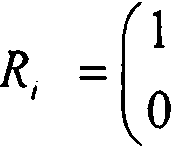
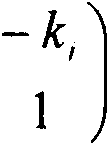
- преломляющая матри

ца z-й границы раздела сред

(*,=

И2

- преломляющая сила

/-й

сферической поверхности, г - ее радиус кривизны; п2, п1 - показатели преломления сред, разделяемых данной поверхностью);

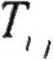
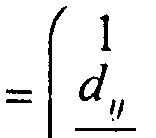
1 - передаточная матрица,

к п

описывающая ход луча в среде с показателем преломления п, заключенной между z-й и j-й преломляющими поверхностями (dij - геометрический путь луча в среде с данным показателем преломления); a, b, с, d- постоянные Гаусса, позволяющие вычислить положения всех кардинальных точек сложной оптической системы.

В среде DELPHI нами создана программа, позволяющая формировать моде

ли оптических систем из заданного набора преломляющих сферических поверхностей и рассчитывать ход параксиальных лучей через эти системы. Параметрами системы, задаваемыми пользователем, являются:

• -    радиусы кривизны преломляющих поверхностей;

• -    расстояния между преломляющими поверхностями;

• -    показатели преломления сред, заключенных между преломляющими поверхностями.

Вычисляемыми параметрами служат координаты главных и фокальных точек моделируемой оптической системы.

По заданным параметрам программа формирует преломляющие и передаточные матрицы системы, вычисляет постоянные Гаусса и координаты кардинальных точек, а также графически изображает ход параксиальных лучей через моделируемую систему.

В программе применен удобный графический интерфейс, позволяющий с помощью мыши перемещать преломляющие поверхности с заданными радиусами кривизны, устанавливать их на нужном расстоянии друг от друга в средах с различными показателями преломления, формируя тем самым модели разнообразных оптических систем.

На рис. 1 приведено изображение основного окна программы.

При последовательном выборе опций «Файл», «Новый» пользователю предоставляется возможность задать параметры моделируемой оптической системы (количество линз, образующих систему, показатели преломления линз и сред между линзами, радиусы кривизны преломляющих поверхностей). При нажатии клавиши «ОК» по заданным параметрам программа фор-

Щ^^^ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ ggggg^^

b2 :/;££ШбШ&ыйй^.з^;1й£Я№й<Й^                                               ^'^x^LJj*]

$айл Опции 2

Рисуем |

D ^. ®     ^ JTt Маштаб 1 [оТ ^j

Рис. 1. Выбор параметров моделируемой системы мирует изображения сферических поверх- гаются на главной оптической оси оптичес-ностей, центры кривизны которых распола- кой системы (рис. 2).

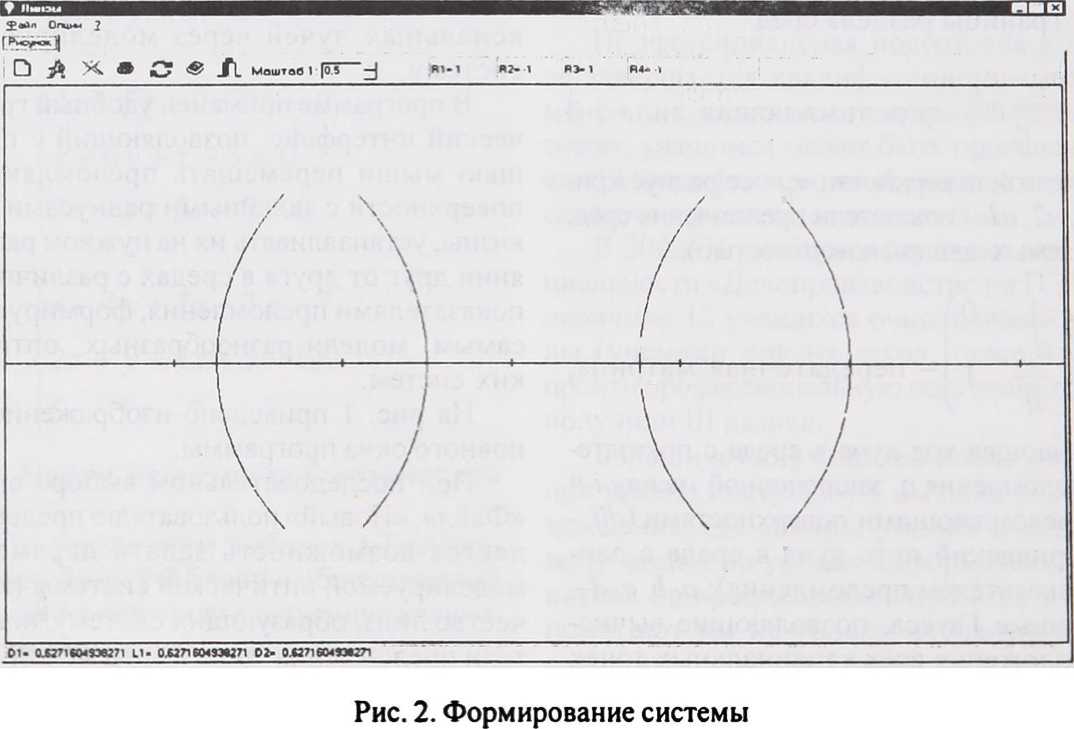
При нажатой пользователем левой кла- верхности могут перемещаться вдоль оп-више «мыши» выбранные сферические по- тической оси. При перемещении поверх-

№№^^           4(2), 2001ЩйЖ^^

ностей постоянно вычисляется расстояние между ними. Установив преломляющие поверхности на необходимом расстоянии друг от друга и учитывая ранее заданные параметры, пользователь формирует мо дель конкретной оптической системы.

При выборе опции «ПУСК (RUN)» программа формирует графическое изображение хода лучей через линзы виртуальной оптической системы и определяет положения ее кардинальных точек и плоскостей (рис. 3).

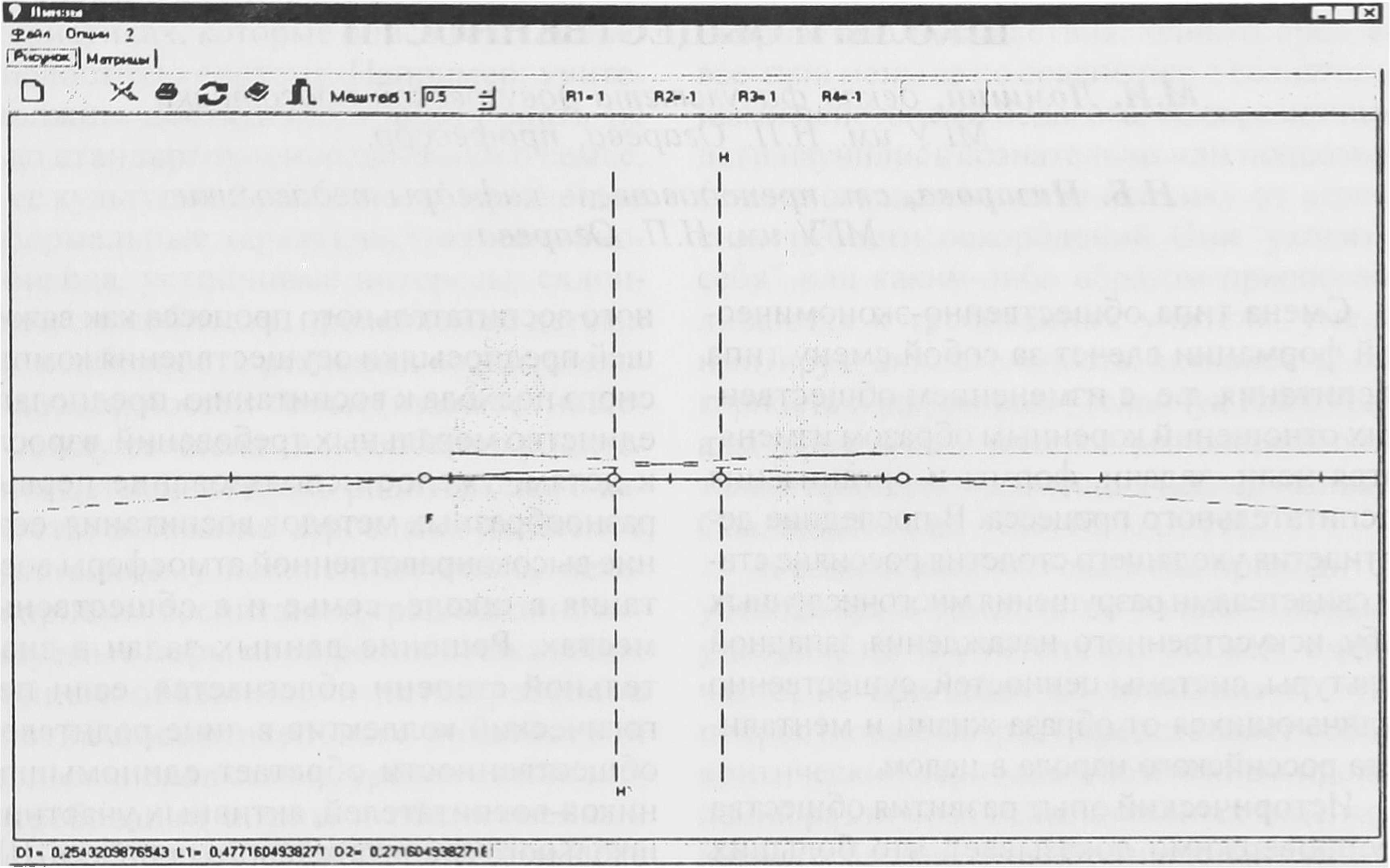
Рис. 3. Изображение хода лучей через систему

Линзы

I О^ГИГГМ Mw> 2

I

0 624

С 673

0 050

1 000 1 630 1 000

1 000

0 616

0 673

0.058

1 000   1 000 1 000   1 000

Г AT^lie^^xwO 3 л**^ггт^ >х*де -HHrvA г^афм'^г.» и

0 254  0 272

0 628

0 673

0 046

0 477

0 620

О6П

Метами!.» i>*w**^«» ей ckcm*

1 000

0 000

i M

-0 630

1.000

I 4.

I

1 000

О ООО

1 000

1 000

0 000

1.000

1 000

0 477

0 000

1 000

1 000

0.000

1.000

I

1 000

0.000

1.000

1 000

0.000

1.000

с- 0.074

Рис. 4. Результаты расчета оптической системы матричным методом